1.1 Numbers

  • Real Number System • Number Line • Absolute Value • Signs of Inequality • Reciprocal • Denominate Numbers • Literal Numbers

In technology and science, as well as in everyday life, we use the very familiar counting numbers, or natural numbers 1, 2, 3, and so on. The whole numbers include 0 as well as all the natural numbers. Because it is necessary and useful to use negative numbers as well as positive numbers in mathematics and its applications, the natural numbers are called the positive integers, and the numbers  − 1 ,  − 2 ,  − 3 ,  and so on are the negative integers.

Therefore, the integers include the positive integers, the negative integers, and zero, which is neither positive nor negative. This means that the integers are the numbers … ,  − 3 ,  − 2 ,  − 1 ,  0, 1, 2, 3, … and so on.

A rational number is a number that can be expressed as the division of one integer a by another nonzero integer b, and can be represented by the fraction a/b. Here a is the numerator and b is the denominator. Here we have used algebra by letting letters represent numbers.

Another type of number, an irrational number, cannot be written in the form of a fraction that is the division of one integer by another integer. The following example illustrates integers, rational numbers, and irrational numbers.

EXAMPLE 1 Identifying rational numbers and irrational numbers

The numbers 5 and  − 19 are integers. They are also rational numbers because they can be written as 51 and  − 191 ,  respectively. Normally, we do not write the 1’s in the denominators.

The numbers 58 and  − 113 are rational numbers because the numerator and the denominator of each are integers.

The numbers 2 and π are irrational numbers. It is not possible to find two integers, one divided by the other, to represent either of these numbers. In decimal form, irrational numbers are nonterminating, nonrepeating decimals. It can be shown that square roots (and other roots) that cannot be expressed exactly in decimal form are irrational. Also, 227 is sometimes used as an approximation for π ,  but it is not equal exactly to π .  We must remember that 227 is rational and π is irrational.

The decimal number 1.5 is rational since it can be written as 32 .  Any such terminating decimal is rational. The number 0.6666 … , where the 6’s continue on indefinitely, is rational because we may write it as 23 .  In fact, any repeating decimal (in decimal form, a specific sequence of digits is repeated indefinitely) is rational. The decimal number 0.6732732732 … is a repeating decimal where the sequence of digits 732 is repeated indefinitely (0.6732732732 …  = 11211665) . 

The rational numbers together with the irrational numbers, including all such numbers that are positive, negative, or zero, make up the real number system (see Fig. 1.1). There are times we will encounter an imaginary number, the name given to the square root of a negative number. Imaginary numbers are not real numbers and will be discussed in Chapter 12. However, unless specifically noted, we will use real numbers. Until Chapter 12, it will be necessary to only recognize imaginary numbers when they occur.

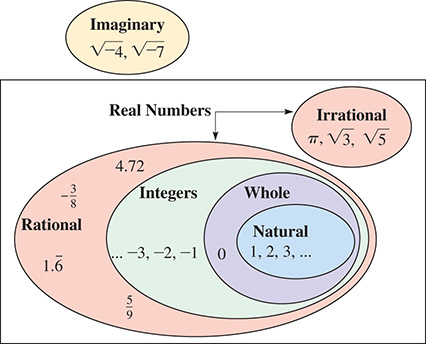
A diagram.

Fig. 1.1

Also in Chapter 12, we will consider complex numbers, which include both the real numbers and imaginary numbers. See Exercise 39 of this section.

EXAMPLE 2 Identifying real numbers and imaginary numbers

  1. The number 7 is an integer. It is also rational because 7 = 71 ,  and it is a real number since the real numbers include all the rational numbers.

  2. The number 3π is irrational, and it is real because the real numbers include all the irrational numbers.

  3. The numbers  − 10 and  −  − 7 are imaginary numbers.

  4. The number  − 37 is rational and real. The number  − 7 is irrational and real.

  5. The number π6 is irrational and real. The number  − 32 is imaginary.

A fraction may contain any number or symbol representing a number in its numerator or in its denominator. The fraction indicates the division of the numerator by the denominator, as we previously indicated in writing rational numbers. Therefore, a fraction may be a number that is rational, irrational, or imaginary.

EXAMPLE 3 Fractions

  1. The numbers 27 and  − 32 are fractions, and they are rational.

  2. The numbers 29 and 6π are fractions, but they are not rational numbers. It is not possible to express either as one integer divided by another integer.

  3. The number  − 56 is a fraction, and it is an imaginary number.

THE NUMBER LINE

Real numbers may be represented by points on a line. We draw a horizontal line and designate some point on it by O, which we call the origin (see Fig. 1.2). The integer zero is located at this point. Equal intervals are marked to the right of the origin, and the positive integers are placed at these positions. The other positive rational numbers are located between the integers. The points that cannot be defined as rational numbers represent irrational numbers. We cannot tell whether a given point represents a rational number or an irrational number unless it is specifically marked to indicate its value.

A number line.

Fig. 1.2

The negative numbers are located on the number line by starting at the origin and marking off equal intervals to the left, which is the negative direction. As shown in Fig. 1.2, the positive numbers are to the right of the origin and the negative numbers are to the left of the origin. Representing numbers in this way is especially useful for graphical methods.

We next define another important concept of a number. The absolute value of a positive number is the number itself, and the absolute value of a negative number is the corresponding positive number. On the number line, we may interpret the absolute value of a number as the distance (which is always positive) between the origin and the number. Absolute value is denoted by writing the number between vertical lines, as shown in the following example.

EXAMPLE 4 Absolute value

The absolute value of 6 is 6, and the absolute value of  − 7 is 7. We write these as | 6|  = 6 and |  − 7|  = 7. See Fig. 1.3.

A number line. From 0 to negative 7 is labeled, absolute value of negative 7 = 7. It is 7 units. From 0 to 6 is labeled, absolute value of 6 = 6. It is 6 units.

Fig. 1.3

Other examples are | 75|  = 75 ,  |  − 2|  = 2 ,  | 0|  = 0 ,  − | π|  =  − π ,  |  − 5.29|  = 5.29 ,  and  − |  − 9|  =  − 9 since |  − 9|  = 9.

On the number line, if a first number is to the right of a second number, then the first number is said to be greater than the second. If the first number is to the left of the second, it is less than the second number. The symbol  >  designates “is greater than,” and the symbol  <  designates “is less than.” These are called signs of inequality. See Fig. 1.4.

EXAMPLE 5 Signs of inequality

A number line and diagram.

Fig. 1.4

Every number, except zero, has a reciprocal. The reciprocal of a number is 1 divided by the number.

EXAMPLE 6 Reciprocal

The reciprocal of 7 is 17 .  The reciprocal of 23 is

An equation reads, start fraction 1 divided by 2 thirds = 1 times 3 halves = 3 halves. Invert denominator, and multiply, from arithmetic.

The reciprocal of 0.5 is 10.5 = 2. The reciprocal of  − π is  − 1π .  Note that the negative sign is retained in the reciprocal of a negative number.

We showed the multiplication of 1 and 32 as 1 × 32 .  We could also show it as 1 ⋅ 32 or 1(32) .  We will often find the form with parentheses is preferable.

In applications, numbers that represent a measurement and are written with units of measurement are called denominate numbers. The next example illustrates the use of units and the symbols that represent them.

EXAMPLE 7 Denominate numbers

  1. To show that a certain TV weighs 62 pounds, we write the weight as 62 lb.

  2. To show that a giant redwood tree is 330 feet high, we write the height as 300 ft.

  3. To show that the speed of a rocket is 1500 meters per second, we write the speed as 1500 m/s. (Note the use of s for second. We use s rather than sec.)

  4. To show that the area of a computer chip is 0.75 square inch, we write the area as 0.75 in . 2 .  (We will not use sq in.)

  5. To show that the volume of water in a glass tube is 25 cubic centimeters, we write the volume as 25 cm3 .  (We will not use cu cm nor cc.)

It is usually more convenient to state definitions and operations on numbers in a general form. To do this, we represent the numbers by letters, called literal numbers. For example, if we want to say “If a first number is to the right of a second number on the number line, then the first number is greater than the second number,” we can write “If a is to the right of b on the number line, then a > b . ” Another example of using a literal number is “The reciprocal of n is 1/n.”

Certain literal numbers may take on any allowable value, whereas other literal numbers represent the same value throughout the discussion. Those literal numbers that may vary in a given problem are called variables, and those literal numbers that are held fixed are called constants.

EXAMPLE 8 Variables and constants

  1. The resistance of an electric resistor is R. The current I in the resistor equals the voltage V divided by R, written as I = V / R .  For this resistor, I and V may take on various values, and R is fixed. This means I and V are variables and R is a constant. For a different resistor, the value of R may differ.

  2. The fixed cost for a calculator manufacturer to operate a certain plant is b dollars per day, and it costs a dollars to produce each calculator. The total daily cost C to produce n calculators is

    C = an + b

    Here, C and n are variables, and a and b are constants, and the product of a and n is shown as an. For another plant, the values of a and b would probably differ.

    If specific numerical values of a and b are known, say a = $7 per calculator and b = $3000 ,  then C = 7n + 3000. Thus, constants may be numerical or literal.

EXERCISES 1.1

In Exercises 1–4, make the given changes in the indicated examples of this section, and then answer the given questions.

  1. In the first line of Example 1, change the 5 to  − 7 and the  − 19 to 12. What other changes must then be made in the first paragraph?

  2. In Example 4, change the 6 to  − 6. What other changes must then be made in the first paragraph?

  3. In the left figure of Example 5, change the 2 to  − 6. What other changes must then be made?

  4. In Example 6, change the 23 to 32 .  What other changes must then be made?

In Exercises 5–8, designate each of the given numbers as being an integer, rational, irrational, real, or imaginary. (More than one designation may be correct.)

  1. 3,  − 4

  2. 73 ,  − 6

  3.  − π6 ,  18

  4.  −  − 6 ,  − 2.33

In Exercises 9 and 10, find the absolute value of each real number.

  1. 3,  − 3 ,  π4 ,   − 1

  2.  − 0.857 ,  2 ,  − 194 ,   − 5 − 2

In Exercises 11–18, insert the correct sign of inequality ( >  or  < ) between the given numbers.

  1. 6  8

  2. 7  5

  3. π  3.1416

  4.  − 4  0

  5.  − 4 − |  − 3| 

  6.  − 2 − 1.42

  7.  − 23 − 34

  8.  − 0.6  0.2

In Exercises 19 and 20, find the reciprocal of each number.

  1. 3 ,  − 43 , yb

  2.  − 13 ,  0.25, 2x

In Exercises 21 and 22, locate (approximately) each number on a number line as in Fig. 1.2.

  1. 2.5 ,  − 125 , 3 ,  − 34

  2.  − 22 , 2π , 12319 ,  − 73

In Exercises 23–46, solve the given problems. Refer to Appendix B for units of measurement and their symbols.

  1. Is an absolute value always positive? Explain.

  2. Is  − 2.17 rational? Explain.

  3. What is the reciprocal of the reciprocal of any positive or negative number?

  4. Is the repeating decimal 2.72¯  rational or irrational?

  5. True or False: A nonterminating, nonrepeating decimal is an irrational number.

  6. If b > a and a > 0 ,  is | b − a|  < | b|  − | a|  ? 

  7. List the following numbers in numerical order, starting with the smallest:  − 1 ,  9 , π , 5 ,  |  − 8|  ,  − |  − 3|  ,  − 3.1.

  8. List the following numbers in numerical order, starting with the smallest: 15 ,  − 10 ,  − |  − 6|  ,  − 4 ,  0.25 ,  |  − π|  . 

  9. If a and b are positive integers and b > a ,  what type of number is represented by the following?

    1. b − a

    2. a − b

    3. b − ab + a

  10. If a and b represent positive integers, what kind of number is represented by (a) a + b ,  (b) a/b, and (c) a × b ? 

  11. For any positive or negative integer: (a) Is its absolute value always an integer? (b) Is its reciprocal always a rational number?

  12. For any positive or negative rational number: (a) Is its absolute value always a rational number? (b) Is its reciprocal always a rational number?

  13. Describe the location of a number x on the number line when (a) x > 0 and (b) x <  − 4.

  14. Describe the location of a number x on the number line when (a) | x|  < 1 and (b) | x|  > 2.

  15. For a number x > 1 ,  describe the location on the number line of the reciprocal of x.

  16. For a number x < 0 ,  describe the location on the number line of the number with a value of | x|  . 

  17. A complex number is defined as a + bj ,  where a and b are real numbers and j =  − 1 .  For what values of a and b is the complex number a + bj a real number? (All real numbers and all imaginary numbers are also complex numbers.)

  18. A sensitive gauge measures the total weight w of a container and the water that forms in it as vapor condenses. It is found that w = c0.1t + 1 ,  where c is the weight of the container and t is the time of condensation. Identify the variables and constants.

  19. In an electric circuit, the reciprocal of the total capacitance of two capacitors in series is the sum of the reciprocals of the capacitances (1CT = 1C1 + 1C2) .  Find the total capacitance of two capacitances of 0.0040 F and 0.0010 F connected in series.

  20. Alternating-current (ac) voltages change rapidly between positive and negative values. If a voltage of 100 V changes to  − 200 V ,  which is greater in absolute value?

  21. The memory of a certain computer has a bits in each byte. Express the number N of bits in n kilobytes in an equation. (A bit is a single digit, and bits are grouped in bytes in order to represent special characters. Generally, there are 8 bits per byte. If necessary, see Appendix B for the meaning of kilo.)

  22. The computer design of the base of a truss is x ft long. Later it is redesigned and shortened by y in. Give an equation for the length L, in inches, of the base in the second design.

  23. In a laboratory report, a student wrote " − 20 ° C >  − 30 ° C . " Is this statement correct? Explain.

  24. After 5 s, the pressure on a valve is less than 60 lb / in.2 (pounds per square inch). Using t to represent time and p to represent pressure, this statement can be written “for t > 5 s, p < 60 lb / in.2 . ” In this way, write the statement “when the current I in a circuit is less than 4 A, the resistance R is greater than 12 Ω (ohms).”

Answers to Practice Exercises

  1. 4.2

  2.  − 34

  3.  < 

  4.  > 

    1.  − 14

    2. 83

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.116.40.177