Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

16.4 Matrices and Linear Equations

Multiply Matrix of Constants by Inverse of Matrix of Coefficients • Solving Systems of Equations • Matrix Solution on a Calculator

As we stated at the beginning of Section 16.1, matrices can be used to solve systems of equations. In this section, we show one method by which this is done. As we develop this method, it will be apparent that there is a great deal of numerical work involved. However, methods such as this one are easily programmed for use on a computer, which can do the arithmetic work very rapidly. Also, most calculators can perform these operations, and we will show an example at the end of the section in which a calculator is used to solve a system of four equations more readily than with earlier methods. It is the method of solving the system of equations that is of primary importance here.

Let us consider the system of equations

\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}

$\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$

Recalling the definition of equality of matrices, we can write this system as

[\begin{array}{c} a_{1} x + b_{1} y \\ a_{2} x + b_{2} y \end{array}] = [\begin{array}{l} c_{1} \\ c_{2} \end{array}]

$[\begin{array}{c} a_{1} x + b_{1} y \\ a_{2} x + b_{2} y \end{array}] = [\begin{array}{l} c_{1} \\ c_{2} \end{array}]$ (16.6)

If we let

A = [\begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array}] X = [\begin{array}{l} x \\ y \end{array}] C = [\begin{array}{l} c_{1} \\ c_{2} \end{array}]

$A = [\begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array}] X = [\begin{array}{l} x \\ y \end{array}] C = [\begin{array}{l} c_{1} \\ c_{2} \end{array}]$ (16.7)

the left side of Eq. (16.6) can be written as the product of matrices A and X.

A X = C

$A X = C$ (16.8)

If we now multiply (on the left) each side of this matrix equation by $A^{- 1},$ $A^{- 1},$ we have

A^{- 1} A X = A^{- 1} C

$A^{- 1} A X = A^{- 1} C$

Because $A^{- 1} A = I,$ $A^{- 1} A = I,$ we have

I X = A^{- 1} C

$I X = A^{- 1} C$

However, $I X = X .$ $I X = X .$ Therefore,

X = A^{- 1} C

$X = A^{- 1} C$ (16.9)

NOTE

[Equation (16.9) states that we can solve a system of linear equations by multiplying the one-column matrix of the constants on the right by the inverse of the matrix of the coefficients.]

The result is a one-column matrix whose elements are the required values for the solution.

CAUTION

Note that $X = A^{- 1} C,$ $X = A^{- 1} C,$ and not $C A^{- 1} .$ $C A^{- 1} .$ The order of matrix multiplication must be carefully followed.

EXAMPLE 1 Matrix solution—two equations

Use matrices to solve the system of equations

\begin{array}{rcl} 2 x - y & = & 7 \\ 5 x - 3 y & = & 18 \end{array}

$\begin{array}{rcl} 2 x - y & = & 7 \\ 5 x - 3 y & = & 18 \end{array}$

The matrices for Eq. (16.7), and the matrix equation are

A = [\begin{array}{r} 2 & - 1 \\ 5 & - 3 \end{array}] X = [\begin{array}{r} x \\ y \end{array}] C = [\begin{array}{r} 7 \\ 18 \end{array}] [\begin{array}{r} 2 & - 1 \\ 5 & - 3 \end{array}] [\begin{array}{r} x \\ y \end{array}] = [\begin{array}{r} 7 \\ 18 \end{array}]

$A = [\begin{array}{r} 2 & - 1 \\ 5 & - 3 \end{array}] X = [\begin{array}{r} x \\ y \end{array}] C = [\begin{array}{r} 7 \\ 18 \end{array}] [\begin{array}{r} 2 & - 1 \\ 5 & - 3 \end{array}] [\begin{array}{r} x \\ y \end{array}] = [\begin{array}{r} 7 \\ 18 \end{array}]$

By either of the methods of the previous section, we can determine the inverse of matrix A to be

A^{- 1} = [\begin{array}{l} 3 & - 1 \\ 5 & - 2 \end{array}]

$A^{- 1} = [\begin{array}{l} 3 & - 1 \\ 5 & - 2 \end{array}]$

We now form the matrix product $A^{- 1} C .$ $A^{- 1} C .$

A^{- 1} C = [\begin{array}{r} 3 & - 1 \\ 5 & - 2 \end{array}] [\begin{array}{r} 7 \\ 18 \end{array}] = [\begin{array}{r} 21 - 18 \\ 35 - 36 \end{array}] = [\begin{array}{r} 3 \\ - 1 \end{array}]

$A^{- 1} C = [\begin{array}{r} 3 & - 1 \\ 5 & - 2 \end{array}] [\begin{array}{r} 7 \\ 18 \end{array}] = [\begin{array}{r} 21 - 18 \\ 35 - 36 \end{array}] = [\begin{array}{r} 3 \\ - 1 \end{array}]$

Because $X = A^{- 1} C,$ $X = A^{- 1} C,$ this means that

[\begin{array}{l} x \\ y \end{array}] = [\begin{array}{r} 3 \\ - 1 \end{array}]

$[\begin{array}{l} x \\ y \end{array}] = [\begin{array}{r} 3 \\ - 1 \end{array}]$

Therefore, the required solution is $x = 3$ $x = 3$ and $y = - 1,$ $y = - 1,$ which checks when these values are substituted into the original equations. See the calculator matrix solution shown in Fig. 16.11.

A calculator screen. — Fig. 16.11

Graphing calculator keystrokes: bit.ly/2yDfhhp

Figure 16.11 Full Alternative Text

EXAMPLE 2 Matrix solution two equations—electric current

For the electric circuit shown in Fig. 16.12, the equations used to find the currents (in amperes) $i_{1}$ $i_{1}$ and $i_{2}$ $i_{2}$ are

A circuit where I sub 1 goes through 15.0 volts, 2.30 Ohms. Current I sub 2 goes through 12.5 volts and 1.25 Ohms. Between the currents is 6.45 Ohms. — Fig. 16.12

\begin{array}{l} 2.30 i_{1} + 6.45 (i_{1} + i_{2}) = 15.0 \\ 1.25 i_{2} + 6.45 (i_{1} + i_{2}) = 12.5 \end{array} or \begin{array}{l} 8.75 i_{1} + 6.45 i_{2} = 15.0 \\ 6.45 i_{1} + 7.70 i_{2} = 12.5 \end{array}

$\begin{array}{l} 2.30 i_{1} + 6.45 (i_{1} + i_{2}) = 15.0 \\ 1.25 i_{2} + 6.45 (i_{1} + i_{2}) = 12.5 \end{array} or \begin{array}{l} 8.75 i_{1} + 6.45 i_{2} = 15.0 \\ 6.45 i_{1} + 7.70 i_{2} = 12.5 \end{array}$

Using matrices to solve this system of equations, we set up the matrix A of coefficients, the matrix C of constants, and the matrix X of currents as

A = [\begin{array}{l} 8.75 & 6.45 \\ 6.45 & 7.70 \end{array}] C = [\begin{array}{l} 15.0 \\ 12.5 \end{array}] X = [\begin{array}{l} i_{1} \\ i_{2} \end{array}]

$A = [\begin{array}{l} 8.75 & 6.45 \\ 6.45 & 7.70 \end{array}] C = [\begin{array}{l} 15.0 \\ 12.5 \end{array}] X = [\begin{array}{l} i_{1} \\ i_{2} \end{array}]$

We now find the inverse of A as

A^{- 1} = \frac{1}{8.75 (7.70) - 6.45 (6.45)} [\begin{array}{r} 7.70 & - 6.45 \\ - 6.45 & 8.75 \end{array}] = [\begin{array}{r} 0.2988 & - 0.2503 \\ - 0.2503 & 0.3395 \end{array}]

$A^{- 1} = \frac{1}{8.75 (7.70) - 6.45 (6.45)} [\begin{array}{r} 7.70 & - 6.45 \\ - 6.45 & 8.75 \end{array}] = [\begin{array}{r} 0.2988 & - 0.2503 \\ - 0.2503 & 0.3395 \end{array}]$

Therefore,

\begin{array}{rcl} X = A^{- 1} C & = & [\begin{array}{r} 0.2988 & - 0.2503 \\ - 0.2503 & 0.3395 \end{array}] [\begin{array}{r} 15.0 \\ 12.5 \end{array}] \\ = & [\begin{array}{r} 0.2988 (15.0) - 0.2503 (12.5) \\ - 0.2503 (15.0) + 0.3395 (12.5) \end{array}] = [\begin{array}{r} 1.35 \\ 0.49 \end{array}] \end{array}

$\begin{array}{rcl} X = A^{- 1} C & = & [\begin{array}{r} 0.2988 & - 0.2503 \\ - 0.2503 & 0.3395 \end{array}] [\begin{array}{r} 15.0 \\ 12.5 \end{array}] \\ = & [\begin{array}{r} 0.2988 (15.0) - 0.2503 (12.5) \\ - 0.2503 (15.0) + 0.3395 (12.5) \end{array}] = [\begin{array}{r} 1.35 \\ 0.49 \end{array}] \end{array}$

Therefore, the required currents are $i_{1} = 1.35 A$ $i_{1} = 1.35 A$ and $i_{2} = 0.49 A .$ $i_{2} = 0.49 A .$ These values check when substituted into the original equations.

EXAMPLE 3 Matrix solution—three equations

Use matrices to solve the system of equations

\begin{array}{r} x + 2 y - z = - 4 \\ 3 x + 5 y - z = - 5 \\ - 2 x - y - 2 z = - 5 \end{array}

$\begin{array}{r} x + 2 y - z = - 4 \\ 3 x + 5 y - z = - 5 \\ - 2 x - y - 2 z = - 5 \end{array}$

Setting up matrices A, C, and X, we have

A = [\begin{array}{r} 1 & 2 & - 1 \\ 3 & 5 & - 1 \\ - 2 & - 1 & - 2 \end{array}] C = [\begin{array}{l} - 4 \\ - 5 \\ - 5 \end{array}] X = [\begin{array}{l} x \\ y \\ z \end{array}]

$A = [\begin{array}{r} 1 & 2 & - 1 \\ 3 & 5 & - 1 \\ - 2 & - 1 & - 2 \end{array}] C = [\begin{array}{l} - 4 \\ - 5 \\ - 5 \end{array}] X = [\begin{array}{l} x \\ y \\ z \end{array}]$

Finding $A^{- 1}$ $A^{- 1}$ (see Example 4 of Section 16.3) and solving for X, we have

\begin{array}{rcl} A^{- 1} & = & [\begin{array}{r} \frac{11}{2} & - \frac{5}{2} & - \frac{3}{2} \\ - 4 & 2 & 1 \\ - \frac{7}{2} & \frac{3}{2} & \frac{1}{2} \end{array}] \\ X = A^{- 1} C & = & [\begin{array}{r} \frac{11}{2} & - \frac{5}{2} & - \frac{3}{2} \\ - 4 & 2 & 1 \\ - \frac{7}{2} & \frac{3}{2} & \frac{1}{2} \end{array}] [\begin{array}{r} - 4 \\ - 5 \\ - 5 \end{array}] = [\begin{array}{r} - 2 \\ 1 \\ 4 \end{array}] \end{array}

$\begin{array}{rcl} A^{- 1} & = & [\begin{array}{r} \frac{11}{2} & - \frac{5}{2} & - \frac{3}{2} \\ - 4 & 2 & 1 \\ - \frac{7}{2} & \frac{3}{2} & \frac{1}{2} \end{array}] \\ X = A^{- 1} C & = & [\begin{array}{r} \frac{11}{2} & - \frac{5}{2} & - \frac{3}{2} \\ - 4 & 2 & 1 \\ - \frac{7}{2} & \frac{3}{2} & \frac{1}{2} \end{array}] [\begin{array}{r} - 4 \\ - 5 \\ - 5 \end{array}] = [\begin{array}{r} - 2 \\ 1 \\ 4 \end{array}] \end{array}$

Thix means that $x = - 2, y = 1,$ $x = - 2, y = 1,$ and $z = 4.$ $z = 4.$

EXAMPLE 4 Matrix solution on a calculator—4 equations

Use a calculator to perform the necessary matrix operations in solving the following

\begin{array}{rcrcrcrcr} 2 r & + & 4 s & - & t & + & u & = & 5 \\ r & - & 2 s & + & 3 t & - & u & = & - 4 \\ 3 r & + & s & + & 2 t & - & 4 u & = & 8 \\ 4 r & + & 5 s & - & t & + & 3 u & = & - 1 \end{array}

$\begin{array}{rcrcrcrcr} 2 r & + & 4 s & - & t & + & u & = & 5 \\ r & - & 2 s & + & 3 t & - & u & = & - 4 \\ 3 r & + & s & + & 2 t & - & 4 u & = & 8 \\ 4 r & + & 5 s & - & t & + & 3 u & = & - 1 \end{array}$

First, we set up matrices A, X, and C:

A = [\begin{array}{r} 2 & 4 & - 1 & 1 \\ 1 & - 2 & 3 & - 1 \\ 3 & 1 & 2 & - 4 \\ 4 & 5 & - 1 & 3 \end{array}] X = [\begin{array}{r} r \\ s \\ t \\ u \end{array}] C = [\begin{array}{r} 5 \\ - 4 \\ 8 \\ - 1 \end{array}]

$A = [\begin{array}{r} 2 & 4 & - 1 & 1 \\ 1 & - 2 & 3 & - 1 \\ 3 & 1 & 2 & - 4 \\ 4 & 5 & - 1 & 3 \end{array}] X = [\begin{array}{r} r \\ s \\ t \\ u \end{array}] C = [\begin{array}{r} 5 \\ - 4 \\ 8 \\ - 1 \end{array}]$

It is now necessary only to enter matrices A and C in the calculator and find the matrix product $A^{- 1} C,$ $A^{- 1} C,$ as shown in Fig. 16.13(a). (There is no need to record or display $A^{- 1} .$ $A^{- 1} .$ ) This shows that the solution is

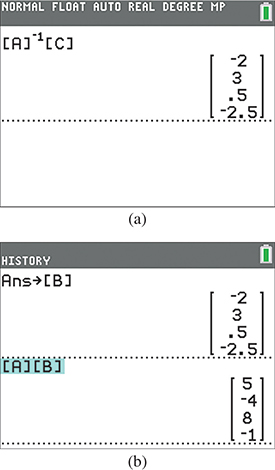
Two calculator screens. — Fig. 16.13

Graphing calculator keystrokes: bit.ly/2IVdskE

Figure 16.13 Full Alternative Text

r = - 2 s = 3 t = 0.5 u = - 2.5

$r = - 2 s = 3 t = 0.5 u = - 2.5$

This solution can be checked on the calculator by storing the resulting matrix X as matrix B and finding the matrix product AB, which should equal matrix C as shown in Fig. 16.13(b). The product AB is equivalent to substituting each value into the original equations, as shown in Eq. (16.8).

EXERCISES 16.4

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the systems of equations.

In Example 1, change the 18 to 19 and then solve the system of equations.
In Example 3, change the $- 4$ $- 4$ in the top equation to $- 2$ $- 2$ and then solve the system of equations.

In Exercises 3–8, solve the given systems of equations by using the inverse of the coefficient matrix. The numbers in parentheses refer to exercises from Section 16.3, where the inverses may be checked.

$\begin{array}{l} 2 x - 3 y = - 6 (3) \\ - 2 x + 4 y = 11 \end{array}$ $\begin{array}{l} 2 x - 3 y = - 6 (3) \\ - 2 x + 4 y = 11 \end{array}$
$\begin{array}{l} - x + 5 y = 4 (5) \\ 4 x + 10 y = - 4 \end{array}$ $\begin{array}{l} - x + 5 y = 4 (5) \\ 4 x + 10 y = - 4 \end{array}$
$\begin{array}{l} x + 2 y = 7 (11) \\ 2 x + 5 y = 11 \end{array}$ $\begin{array}{l} x + 2 y = 7 (11) \\ 2 x + 5 y = 11 \end{array}$
$\begin{array}{l} 2 x + 4 y = - 9 (13) \\ - x - y = 2 \end{array}$ $\begin{array}{l} 2 x + 4 y = - 9 (13) \\ - x - y = 2 \end{array}$
$\begin{array}{l} x - 3 y - 2 z = - 8 (17) \\ - 2 x + 7 y + 3 z = 19 \\ x - y - 3 z = - 3 \end{array}$ $\begin{array}{l} x - 3 y - 2 z = - 8 (17) \\ - 2 x + 7 y + 3 z = 19 \\ x - y - 3 z = - 3 \end{array}$
$\begin{array}{l} x + 3 y + 2 z = 5 (19) \\ - 2 x - 5 y - z = - 1 \\ 2 x + 4 y = - 2 \end{array}$ $\begin{array}{l} x + 3 y + 2 z = 5 (19) \\ - 2 x - 5 y - z = - 1 \\ 2 x + 4 y = - 2 \end{array}$

In Exercises 9–16. solve the given systems of equations by using the inverse of the coefficient matrix

$\begin{array}{l} 2 x - 3 y = 3 \\ 4 x - 5 y = 4 \end{array}$ $\begin{array}{l} 2 x - 3 y = 3 \\ 4 x - 5 y = 4 \end{array}$
$\begin{array}{l} x + 2 y = 3 \\ 3 x + 4 y = 11 \end{array}$ $\begin{array}{l} x + 2 y = 3 \\ 3 x + 4 y = 11 \end{array}$
$\begin{array}{l} 2.5 x + 2.8 y = - 3.0 \\ 3.5 x - 1.6 y = 9.6 \end{array}$ $\begin{array}{l} 2.5 x + 2.8 y = - 3.0 \\ 3.5 x - 1.6 y = 9.6 \end{array}$
$\begin{array}{l} 24 x - 10 y = - 800 \\ 31 x + 25 y = 180 \end{array}$ $\begin{array}{l} 24 x - 10 y = - 800 \\ 31 x + 25 y = 180 \end{array}$
$\begin{array}{l} x + 2 y + 2 z = - 4 \\ 4 x + 9 y + 10 z = - 18 \\ - x + 3 y + 7 z = - 7 \end{array}$ $\begin{array}{l} x + 2 y + 2 z = - 4 \\ 4 x + 9 y + 10 z = - 18 \\ - x + 3 y + 7 z = - 7 \end{array}$
$\begin{array}{l} x - 4 y - 2 z = - 7 \\ - x + 5 y + 5 z = 18 \\ 3 x - 7 y + 10 z = 38 \end{array}$ $\begin{array}{l} x - 4 y - 2 z = - 7 \\ - x + 5 y + 5 z = 18 \\ 3 x - 7 y + 10 z = 38 \end{array}$
$\begin{array}{l} 2 x + 4 y + z = 5 \\ - 2 x - 2 y - z = - 6 \\ - x + 2 y + z = 0 \end{array}$ $\begin{array}{l} 2 x + 4 y + z = 5 \\ - 2 x - 2 y - z = - 6 \\ - x + 2 y + z = 0 \end{array}$
$\begin{array}{l} 4 x + y = 2 \\ - 2 x - y + 3 z = - 18 \\ 2 x + y - z = 8 \end{array}$ $\begin{array}{l} 4 x + y = 2 \\ - 2 x - y + 3 z = - 18 \\ 2 x + y - z = 8 \end{array}$

In Exercises 17–28, solve the given systems of equations by using the inverse of the coefficient matrix. Use a calculator to perform the necessary matrix operations and display the results and the check. See Example 4.

$\begin{array}{l} 3 x - y = 4 \\ 7 x + 2 y = 18 \end{array}$ $\begin{array}{l} 3 x - y = 4 \\ 7 x + 2 y = 18 \end{array}$
$\begin{array}{l} 5 s + 2 t = 1 \\ s - 3 t = 7 \end{array}$ $\begin{array}{l} 5 s + 2 t = 1 \\ s - 3 t = 7 \end{array}$
$\begin{array}{l} 3 x - 2 y = 5 \\ 9 x + 4 y = - 5 \end{array}$ $\begin{array}{l} 3 x - 2 y = 5 \\ 9 x + 4 y = - 5 \end{array}$
$\begin{array}{l} 4 u + 3 v = 7 \\ 6 u - 2 v = - 9 \end{array}$ $\begin{array}{l} 4 u + 3 v = 7 \\ 6 u - 2 v = - 9 \end{array}$
$\begin{array}{l} 2 x - y - z = 7 \\ 4 x - 3 y + 2 z = 4 \\ 3 x + 5 y + z = - 10 \end{array}$ $\begin{array}{l} 2 x - y - z = 7 \\ 4 x - 3 y + 2 z = 4 \\ 3 x + 5 y + z = - 10 \end{array}$
$\begin{array}{l} 6 x + 2 y + 9 z = 13 \\ 7 x + 6 y - 6 z = 6 \\ 5 x - 4 y + 3 z = 15 \end{array}$ $\begin{array}{l} 6 x + 2 y + 9 z = 13 \\ 7 x + 6 y - 6 z = 6 \\ 5 x - 4 y + 3 z = 15 \end{array}$
$\begin{array}{l} u - 3 v - 2 w = 9 \\ 3 u + 2 v + 6 w = 20 \\ 4 u - v + 3 w = 25 \end{array}$ $\begin{array}{l} u - 3 v - 2 w = 9 \\ 3 u + 2 v + 6 w = 20 \\ 4 u - v + 3 w = 25 \end{array}$
$\begin{array}{l} 4 x + 2 y - 2 z = 2 \\ 3 x - 2 y - 8 z = - 3 \\ x + 3 y + z = 10 \end{array}$ $\begin{array}{l} 4 x + 2 y - 2 z = 2 \\ 3 x - 2 y - 8 z = - 3 \\ x + 3 y + z = 10 \end{array}$
$\begin{array}{l} x - 5 y + 2 z - t = - 18 \\ 3 x + y - 3 z + 2 t = 17 \\ 4 x - 2 y + z - t = - 1 \\ - 2 x + 3 y - z + 4 t = 11 \end{array}$ $\begin{array}{l} x - 5 y + 2 z - t = - 18 \\ 3 x + y - 3 z + 2 t = 17 \\ 4 x - 2 y + z - t = - 1 \\ - 2 x + 3 y - z + 4 t = 11 \end{array}$
$\begin{array}{l} 2 p + q + 5 r + s = 5 \\ p + q - 3 r - 4 s = - 1 \\ 3 p + 6 q - 2 r + s = 8 \\ 2 p + 2 q + 2 r - 3 s = 2 \end{array}$ $\begin{array}{l} 2 p + q + 5 r + s = 5 \\ p + q - 3 r - 4 s = - 1 \\ 3 p + 6 q - 2 r + s = 8 \\ 2 p + 2 q + 2 r - 3 s = 2 \end{array}$
$\begin{array}{l} 2 v + 3 w + x - y - 2 z = 6 \\ 6 v - 2 w - x + 3 y - z = 21 \\ v + 3 w - 4 x + 2 y + 3 z = - 9 \\ 3 v - w - x + 7 y + 4 z = 5 \\ v + 6 w + 6 x - 4 y - z = - 4 \end{array}$ $\begin{array}{l} 2 v + 3 w + x - y - 2 z = 6 \\ 6 v - 2 w - x + 3 y - z = 21 \\ v + 3 w - 4 x + 2 y + 3 z = - 9 \\ 3 v - w - x + 7 y + 4 z = 5 \\ v + 6 w + 6 x - 4 y - z = - 4 \end{array}$
$\begin{array}{l} 4 x - y + 2 z - 2 t + u = - 15 \\ 8 x + y - z + 4 t - 2 u = 26 \\ 2 x - 6 y - 2 z + t - u = 10 \\ 2 x + 5 y + z - 3 t + 8 u = - 22 \\ 4 x - 3 y + 2 z + 4 t + 2 u = - 4 \end{array}$ $\begin{array}{l} 4 x - y + 2 z - 2 t + u = - 15 \\ 8 x + y - z + 4 t - 2 u = 26 \\ 2 x - 6 y - 2 z + t - u = 10 \\ 2 x + 5 y + z - 3 t + 8 u = - 22 \\ 4 x - 3 y + 2 z + 4 t + 2 u = - 4 \end{array}$

In Exercises 29–40, solve the indicated systems of equations using the inverse of the coefficient matrix. In Exercises 35–40, it is necessary to set up the appropriate equations.

For the following system of equations, solve for $x^{2}$ $x^{2}$ and y using the matrix methods of this section, and then solve for x and y.

$\begin{array}{rcr} x^{2} + y & = & 2 \\ 2 x^{2} - y & = & 10 \end{array}$ $\begin{array}{rcr} x^{2} + y & = & 2 \\ 2 x^{2} - y & = & 10 \end{array}$
For the following system of equations, solve for $x^{2}$ $x^{2}$ and $y^{2}$ $y^{2}$ using the matrix methods of this scction, and then solve for x and y.

$\begin{array}{rcr} x^{2} - y^{2} & = & 8 \\ x^{2} + y^{2} & = & 10 \end{array}$ $\begin{array}{rcr} x^{2} - y^{2} & = & 8 \\ x^{2} + y^{2} & = & 10 \end{array}$
Solve any pair of the system of equations $2 x - y = 4, 3 x + y = 1,$ $2 x - y = 4, 3 x + y = 1,$ and $x - 2 y = 5.$ $x - 2 y = 5.$ Show that the solution is valid for any pair chosen. What conclusions can be drawn about the graphs of the three equations?
In solving the system of equations $3 x - 4 y = 5, 8 y - 6 x = 7,$ $3 x - 4 y = 5, 8 y - 6 x = 7,$ when conclusion can be drawn?
Forces $F_{1}$ $F_{1}$ and $F_{2}$ $F_{2}$ hold up a beam that weights 2540 N, as shown in Fig. 16.14. The equations used to find the forces are

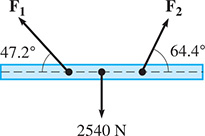
Fig. 16.14

$\begin{array}{l} A \sin 47.2 ° + B \sin 64.4 ° = 2540 \\ A \cos 47.2 ° - B \cos 64.4 ° = 0 \end{array}$ $\begin{array}{l} A \sin 47.2 ° + B \sin 64.4 ° = 2540 \\ A \cos 47.2 ° - B \cos 64.4 ° = 0 \end{array}$

Find the magnitude of each force.
In applying Kirchhoff’s laws to the circuit shown in Fig. 16.15, following equations are found. Determine the indicated currents (in A).

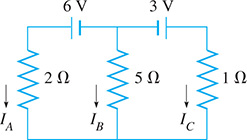
Fig. 16.15

$\begin{array}{rcrcrcl} I_{A} & + & I_{B} & + & I_{C} & = & 0 \\ 2 I_{A} & - & 5 I_{B} & = & 6 \\ 5 I_{B} & - & I_{C} & = & - 3 \end{array}$ $\begin{array}{rcrcrcl} I_{A} & + & I_{B} & + & I_{C} & = & 0 \\ 2 I_{A} & - & 5 I_{B} & = & 6 \\ 5 I_{B} & - & I_{C} & = & - 3 \end{array}$
Two batteries in an electric circuit have a combined voltage of 18 V, and one battery produces 6 V less than twice the other. What is the voltage of each?
For college expenses, a student took out a loan at 4.00%, and a semester later took out a second loan at 3.00%. The total annual interest for the two loans was $245. If the second loan had been for twice as much, the annual interest would have been $290. How much was each loan?
What volume of each of a 20% acid solution and a 50% acid solution should be combined to form 48 mL of a 25% solution?
Two computer programs together require 236 MB (megabytes) of memory. If one program requires 20.0 MB of memory more than twice the memory of the other, what are the memory requirements of each program?
A research chemist wants to make 10.0 L of gasoline containing 2.0% of a new experimental additive. Gasoline without additive and two mixtures of gasoline with additive, one with 5.0% and the other with 6.0%, are to be used. If four times as much gasoline without additive as the 5.0% mixture is to be used, how much of each is needed?
A river tour boat takes 5.0 h to cruise downstream and 7.0 h for the return upstream. If the river flows at 4.0 mi/h, how fast does the boat travel in still water, and how far downstream does the boat go before starting the return trip?

Answer to Practice Exercise

$x = 3, y = - 1$ $x = 3, y = - 1$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 16.4 Matrices and Linear Equations

Create new playlist

Sign In

Sign Up

Table of Contents for
16.4 Matrices and Linear Equations