5.5 Solving Systems of Three Linear Equations in Three Unknowns Algebraically

  • Algebraic Method Using Addition or Subtraction • Solving a System Using Reduced Row Echelon Form

Many technical problems involve systems of linear equations with more than two unknowns. In this section, we solve systems with three unknowns, and in Chapter 16 we will show how systems with even more unknowns are solved.

Solving such systems is very similar to solving systems in two unknowns. In this section, we will show the algebraic method, and in the next section we will show how determinants are used. Graphical solutions are not used since a linear equation in three unknowns represents a plane in space. We will, however, briefly show graphical interpretations of systems of three linear equations at the end of this section.

A system of three linear equations in three unknowns written in the form

a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3
(5.10)

has as its solution the set of values x, y, and z that satisfy all three equations simultaneously. The method of solution involves multiplying two of the equations by the proper numbers to eliminate one of the unknowns between these equations. We then repeat this process, using a different pair of the original equations, being sure that we eliminate the same unknown as we did between the first pair of equations. At this point we have two linear equations in two unknowns that can be solved by any of the methods previously discussed.

EXAMPLE 1 Algebraically solving a system

Solve the following system of equations:

(1)4x + y + 3z = 1(2)2x − 2y + 6z = 11(3) − 6x + 3y + 12z =  − 4_ (4)8x + 2y + 6z = 22x − 2y + 6z = 11_ ( 1)  multiplied by 2( 2) (5)10x + 12z = 13adding_ (6)12x + 3y + 9z = 3 − 6x + 3y + 12z =  − 4_ ( 1)  multiplied by 3( 3) (7)18x − 3z = 7subtracting_ (8)10x + 12z = 1372x − 12z = 28_ ( 5) ( 7)  multiplied by 4(9)82x = 41adding(10)x = 12(11)18(12) − 3z = 7substituting ( 10)  in ( 7) (12) − 3z =  − 2(13)z = 23(14)4(12) + y + 3(23) = 1substituting ( 13)  and ( 10)  in ( 1) (15)2 + y + 2 = 1(16)y =  − 3

Thus, the solution is x = 12 ,  y =  − 3 ,  z = 23 .  Substituting in the equations, we have

4(12) + ( − 3) + 3(23) ? _ _ 12(12) − 2( − 3) + 6(23) ? _ _ 11 − 6(12) + 3( − 3) + 12(23) ? _ _  − 41 = 111 = 11 − 4 =  − 4

We see that the solution checks.

If we had first eliminated x, we would then have had to solve two equations in y and z. If we had first eliminated z, we would then have had to solve two equations in x and y. In each case, the basic procedure is the same.

EXAMPLE 2 Setting up and solving a system—voltage

Three voltages, e1 ,  e2 ,  and e3 ,  where e3 is three times e1 ,  are in series with the same polarity [see Fig. 5.37(a)] and have a total voltage of 85 mV. If e2 is reversed in polarity [see Fig. 5.37(b)], the voltage is 35 mV. Find the voltages.

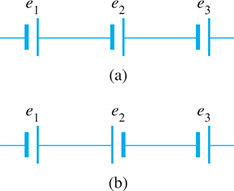
Two series, each with voltages e sub 1, e sub 2, and e sub 3. Series ay has consistent voltage polarities from left to right. Series b has voltage e sub 2 reversed.

Fig. 5.37

Because the voltages are in series with the same polarity, e1 + e2 + e3 = 85 .  Then, since e3 is three times e1 ,  we have e3 = 3e1 .  Then, with the reversed polarity of e2 ,  we have e1 − e2 + e3 = 35 .  Writing these equations in standard form, we have the following solution:

(1)e1 + e2 + e3 = 85(2)3e1 − e3 = 0rewriting second equation(3)e1 − e2 + e3 = 35_ (4)2e1 + 2e3 = 120adding ( 1)  and ( 3) (5)6e1 − 2e3 = 0_ ( 2)  multiplied by 2(6)8e1 = 120adding(7)e1 = 15 mV(8)3(15) − e3 = 0substituting ( 7)  in ( 2) (9)e3 = 45 mV(10)15 + e2 + 45 = 85substituting ( 7)  and ( 9)  in ( 1) (11)e2 = 25 mV

Therefore, the three voltages are 15 mV, 25 mV, and 45 mV.

Checking the solution, the sum of the three voltages is 85 mV, e3 is three times e1 ,  and the sum of e1 and e3 less e2 is 35 mV.

A calculator can be used to solve a system of equations using the reduced row echelon form (rref) feature. It is programmed to perform the same row operations that we use, and it continues until all the unknowns are isolated, making the solutions clear. The difference is that the calculator performs the operations on the numerical values only (without the variables), which are entered into an array with rows and columns called a matrix. The following example illustrates this process.

EXAMPLE 3 Solving a system using rref—robotic forces

The forces acting on the main link of an industrial robotic arm are shown in Fig. 5.38. An analysis of the forces leads to the following system of equations. Determine the forces.

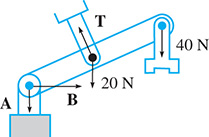
A diagram of a robotic arm that rises.

Fig. 5.38

A + 60 = 0.8TB = 0.6T8A + 6B + 80 = 5TA − 0.8T =  − 60B − 0.6T = 08A + 6B − 5T =  − 80 [ 10 − 0.8 − 6001 − 0.6086 − 5 − 80 ]  [ 10040104800180 ] 1. Write the system in the form of Eqs. ( 5.10) , lining upthe variables, equal signs, and constants.2. Construct a matrix with 3 rows and 4 columns that includesthe coefficients and constants, but not the variables.This is called an augmented matrix. Insert zerosfor missing terms. The dotted line represents the equalsign. Enter this into a calculator using the Matrix > Editfeature. See Fig. 5.39( a)  on the next page.3. Use the Matrix> Math> rref feature to convertthe matrix to reduced row echelon form. In thisform, the solutions for A, B, and T are evident. SeeFig. 5.39( b)  on the next page.

Therefore, the forces are A = 4 N ,  B = 48 N ,  and T = 80 N . 

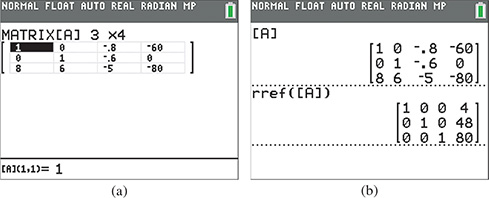
Two calculator screens.

Fig. 5.39

Systems with four or more unknowns are solved in a manner similar to that used for three unknowns. With four unknowns, one is eliminated between three different pairs of equations, and the resulting three equations are then solved.

Linear systems with more than two unknowns may have an unlimited number of solutions or be inconsistent. After eliminating unknowns, if we have 0 = 0 ,  there is an unlimited number of solutions. If we have 0 = a(a ≠ 0) ,  the system is inconsistent, and there is no solution. (See Exercises 33–36.)

As noted earlier, a linear equation in three unknowns represents a plane in space. For three linear equations in three unknowns, if the planes intersect at a point, there is a unique solution [Fig. 5.40(a)]; if they intersect in a line, there is an unlimited number of solutions [Fig. 5.40(b)]. If the planes do not have a common intersection, the system is inconsistent. In inconsistent systems, the planes can be parallel [Fig. 5.41(a)], two can be parallel [Fig. 5.41(b)], or they can intersect in three parallel lines [Fig. 5.41(c)]. If one plane is coincident with another plane, the system has an unlimited number of solutions if they intersect with the third plane, or is inconsistent otherwise.

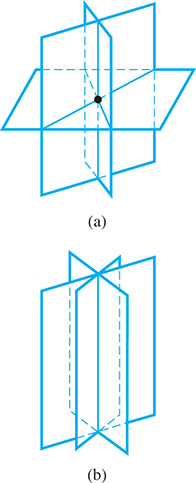
Two diagrams of intersecting planes.

Fig. 5.40

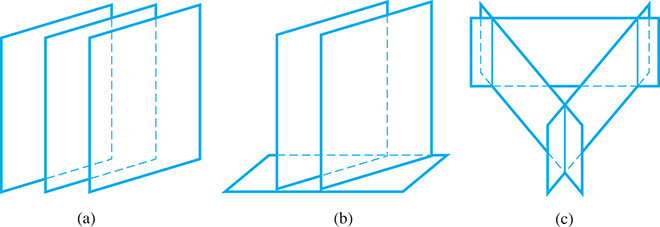
Three diagrams of planes.

Fig. 5.41

EXERCISES 5.5

In Exercises 1 and 2, make the given changes in Example 1 of this section and then solve the resulting system of equations.

  1. In the second equation, change the constant to the right of the  =  sign from 11 to 12, and in the third equation, change the constant to the right of the  =  sign from  − 4 to  − 14 . 

  2. Change the second equation to 8x + 9z = 10 (no y-term).

In Exercises 3–14, solve the given systems of equations.

  1. x + y + z = 2x − z = 1x + y = 1

  2. x + y − z =  − 3x + z = 22x − y + 2z = 3

  3. 2x + 3y + z = 2 − x + 2y + 3z =  − 1 − 3x − 3y + z = 0

  4. 2x + y − z = 44x − 3y − 2z =  − 28x − 2y − 3z = 3

  5. 5l + 6w − 3h = 64l − 7w − 2h =  − 33l + w − 7h = 1

  6. 3r + s − t = 2r + t − 2s = 04r − s + t = 3

  7. 2x − 2y + 3z = 52x + y − 2z =  − 13z + y − 4x = 0

  8. 2u + 2v + 3w = 03u + v + 4w = 21 − u − 3v + 7w = 15

  9. 3x − 7y + 3z = 63x + 3y + 6z = 15x − 5y + 2z = 5

  10. 18x + 24y + 4z = 4663x +  6y − 15z =  − 75 − 90x + 30y − 20z =  − 55

  11. 10x + 15y − 25z = 3540x − 30y − 20z = 1016x − 2y + 8z = 6

  12. 2i1 − 4i2 − 4i3 = 33i1 + 8i2 + 2i3 =  − 114i1 + 6i2 − i3 =  − 8

In Exercises 15–18, solve the given systems of equations using the reduced row echelon form (rref) feature on a calculator. The decimals in Exercises 17–18 are approximate.

  1.  − x + 3y − 2z = 73x + 4y − 7z =  − 8x + 2y + z = 2

  2. 3a + 2b + c = 204a − 10c =  − 10 − a − 2b + 2c =  − 1

  3. I2 = I1 + I38.00I1 + 10.0I2 = 80.06.00I3 + 10.0I2 = 60.0

  4. 1.21x + 1.32y + 1.20z = 6.814.93x − 1.25y + 3.65z = 22.02.85x + 3.25y − 2.70z = 2.76

In Exercises 19 and 20, find the indicated functions.

  1. Find the function f(x) = ax2 + bx + c ,  if f(1) = 3 ,  f( − 2) = 15 ,  and f(3) = 5 . 

  2. Find the function f(x) = ax2 + bx + c ,  if f(1) =  − 3 ,  f( − 3) =  − 35 ,  and f(3) =  − 11 . 

In Exercises 21–32, solve the systems of equations. In Exercises 25–32, it is necessary to set up the appropriate equations. All numbers are accurate to at least three significant digits.

  1. A medical supply company has 1150 worker-hours for production, maintenance, and inspection. Using this and other factors, the number of hours used for each operation, P, M, and I, respectively, is found by solving the following system of equations:

    P + M + I = 1150P = 4I − 100P = 6M + 50

  2. Three oil pumps fill three different tanks. The pumping rates of the pumps (in L/h) are r1 ,  r2 ,  and r3 ,  respectively. Because of malfunctions, they do not operate at capacity each time. Their rates can be found by solving the following system of equations:

    r1 + r2 + r3 = 14 , 000r1 + 2r2 = 13 , 0003r1 + 3r2 + 2r3 = 36 , 000

  3. The forces acting on a certain girder, as shown in Fig. 5.42, can be found by solving the following system of equations:

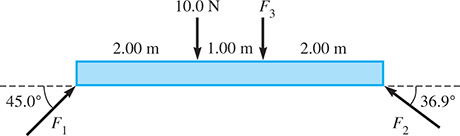
    A horizontal girder.

    Fig. 5.42

    0.707F1 − 0.800F2 = 00.707F1 + 0.600F2 − F3 = 10.03.00F2 − 3.00F3 = 20.0

    Find the forces, in newtons.

  4. Using Kirchhoff’s laws (see the chapter introduction; the equations can be found in most physics textbooks) with the electric circuit shown in Fig. 5.43, the following equations are found. Find the indicated currents (in A) I1 ,  I2 ,  and I3 . 

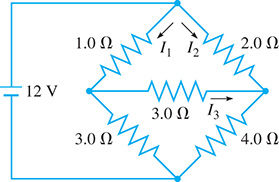
    A circuit with 12 volts where current I sub 1 goes through 1.0 Ohms, and I sub 2 goes through 2.0 Ohms.

    Fig. 5.43

    1.0I1 + 3.0(I1 − I3) = 122.0I2 + 4.0(I2 + I3) = 121.0I1 − 2.0I2 + 3.0I3 = 0

  5. Find angles A, B, and C in the roof truss shown in Fig. 5.44.

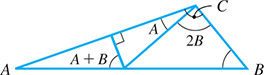
    Triangle Ay B C.

    Fig. 5.44

  6. Under certain conditions, the cost per mile C of operating a car is a function of the speed v (in mi/h) of the car, given by C = av2 + bv + c .  If C = 28 ¢ / mi for v = 10 mi / h ,  C = 22 ¢ / mi for v = 30 mi / h ,  and C = 24 ¢ / mi for v = 50 mi / h ,  find C as a function of v.

  7. In an election with three candidates for mayor, the initial vote count gave A 200 more votes than B, and 500 more votes than C. An error was found, and 1.0% of A’s initial votes went to B, and 2.0% of A’s initial votes went to C, such that B had 100 more votes than C. How many votes did each have in the final tabulation?

  8. A person invests $22,500, partly at 5.00%, partly at 6.00%, the remainder at 6.50%, with a total annual interest of $1308. If the interest received at 5.00% equals the interest received at 6.00%, how much is invested at each rate?

  9. A university graduate school conferred 420 advanced academic degrees at graduation. There were 100 more MA degrees than MS and PhD degrees combined, and 3 times as many MS degrees as PhD degrees. How many of each were awarded?

  10. The computer systems at three weather bureaus have a combined hard-disk memory capacity of 8.0 TB (terabytes). The memory capacity of systems A and C have 0.2 TB more memory than twice that of system B, and twice the sum of the memory capacities of systems A and B is three times that of system C. What are the memory capacities of each of these computer systems?

  11. By weight, one fertilizer is 20% potassium, 30% nitrogen, and 50% phosphorus. A second fertilizer has percents of 10, 20, and 70, respectively, and a third fertilizer has percents of 0, 30, and 70, respectively. How much of each must be mixed to get 200 lb of fertilizer with percents of 12, 25, and 63, respectively?

  12. The average traffic flow (number of vehicles) from noon until 1 p.m. in a certain section of one-way streets in a city is shown in Fig. 5.45. Explain why an analysis of the flow through these intersections is not sufficient to obtain unique values for x, y, and z. Hint: The total traffic going into each intersection equals the traffic going out.

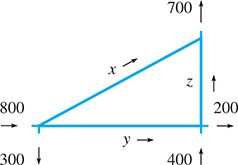
    A triangular diagram.

    Fig. 5.45

In Exercises 33–36, show that the given systems of equations have either an unlimited number of solutions or no solution. If there is an unlimited number of solutions, find one of them.

  1. x − 2y − 3z = 2x − 4y − 13z = 14 − 3x + 5y + 4z = 0

  2. x − 2y − 3z = 2x − 4y − 13z = 14 − 3x + 5y + 4z = 2

  3. 3x + 3y − 2z = 22x − y + z = 1x − 5y + 4z =  − 3

  4. 3x + y − z =  − 3x + y − 3z =  − 5 − 5x − 2y + 3z =  − 7

Answer to Practice Exercise

  1. x = 1/2 ,  y =  − 3 ,  z = 2/3

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.189.2.122