8.4 Applications of Radian Measure
Arc Length on a Circle • Area of a Sector of a Circle • Linear and Angular Velocity
Radian measure has numerous applications in mathematics and technology. In this section, we discuss applications involving circular arc length, the area of a sector, and the relationship between linear and angular velocity.
ARC LENGTH ON A CIRCLE
From geometry, we know that the length of an arc on a circle is proportional to the central angle formed by the radii that intercept the arc. The length of arc of a complete circle is the circumference. Letting s represent the length of arc, we may state that for a complete circle. Because is the central angle (in radians) of the complete circle, the length s of any circular arc with central angle (in radians) is given by
Therefore, if we know the central angle in radians and the radius of a circle, we can find the length of a circular arc directly by using Eq. (8.9). See Fig. 8.33.
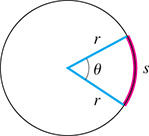
Fig. 8.33
EXAMPLE 1 Arc length
Find the length of arc on a circle of radius for which the central angle See Fig. 8.34.

Fig. 8.34
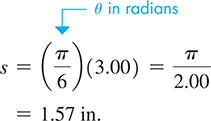
Therefore, the length of arc s is 1.57 in.
Among the important applications of arc length are distances on the Earth’s surface. For most purposes, the Earth may be regarded as a sphere (the diameter at the equator is slightly greater than the distance between the poles). A great circle of the Earth (or any sphere) is the circle of intersection of the surface of the sphere and a plane that passes through the center.
The equator is a great circle and is designated as latitude. Other parallels of latitude are parallel to the equator with diameters decreasing to zero at the poles, which are N and S. See Fig. 8.35.
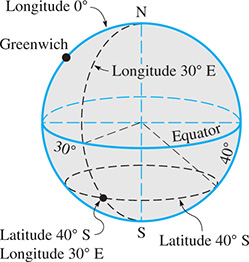
Fig. 8.35
Meridians of longitude are half great circles between the poles. The prime meridian through Greenwich, England, is designated as , with meridians to measured east and west from Greenwich. Positions on the surface of the Earth are designated by longitude and latitude.
EXAMPLE 2 Arc length—nautical mile
The traditional definition of a nautical mile is the length of arc along a great circle of the Earth for a central angle of The modern international definition is a distance of 1852 m. What measurement of the Earth’s radius does this definition use?
Here, and Solving for r, we have
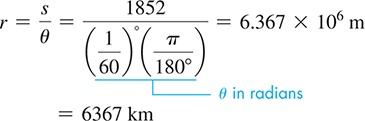
Historically, the fact that the Earth is not a perfect sphere has led to many variations in the distance used for a nautical mile.
AREA OF A SECTOR OF A CIRCLE
Another application of radians is finding the area of a sector of a circle (see Fig. 8.36). Recall from geometry that areas of sectors of circles are proportional to their central angles. The area of a circle is which can be written as Because the angle for a complete circle is the area of any sector of a circle in terms of the radius and central angle (in radians) is

Fig. 8.36
EXAMPLE 3 Area of sector of circle—text messages
Showing that 17.5% of high school students send at least 200 text messages per day on a pie chart of radius 8.50 cm means that the central angle of the sector is (17.5% of ). The area of this sector (see Fig. 8.37) is

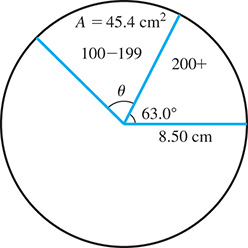
Fig. 8.37
Given that the area of the pie chart in Fig. 8.37 that shows the percent of students who send 100–199 text messages per day is we can find the central angle of this sector by first solving for This gives
This means the central angle is 1.26 rad, or .
CAUTION
We should note again that the equations in this section require that the angle is expressed in radians. A common error is to use in degrees.
LINEAR AND ANGULAR VELOCITY
The average velocity of a moving object is defined by where v is the average velocity, s is the distance traveled, and t is the elapsed time. For an object moving in a circular path with constant speed, the distance traveled is the length of arc through which it moves. Therefore, if we divide both sides of Eq. (8.9) by t, we obtain
where is called the angular velocity and is designated by Therefore,
Equation (8.11) expresses the relationship between the linear velocity v and the angular velocity of an object moving around a circle of radius r. See Fig. 8.38. In the figure, v is shown directed tangent to the circle, for that is its direction for the position shown. The direction of v changes constantly.
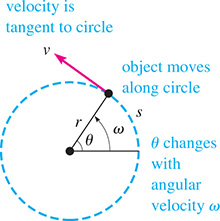
Fig. 8.38
CAUTION
In order to use Eq. (8.11), the units for must be radians per unit time. However, in practice, is often given in revolutions per minute or in some similar unit. In these cases, it is necessary to convert the units of to radians per unit of time before substituting in Eq. (8.11).
EXAMPLE 4 Angular velocity—hang glider motion
A person on a hang glider is moving in a horizontal circular arc of radius 90.0 m with an angular velocity of 0.125 rad/s. The person’s linear velocity is
(Remember that radians are numbers and are not included in the final set of units.) This means that the person is moving along the circumference of the arc at 11.3 m/s (40.7 km/h).
EXAMPLE 5 Angular velocity—satellite orbit
A communications satellite remains at an altitude of 22,320 mi above a point on the equator. If the radius of the Earth is 3960 mi, what is the velocity of the satellite?
In order for the satellite to remain over a point on the equator, it must rotate exactly once each day around the center of the Earth (and it must remain at an altitude of 22,320 mi). Because there are radians in each revolution, the angular velocity is
The radius of the circle through which the satellite moves is its altitude plus the radius of the Earth, or Thus, the velocity is
EXAMPLE 6 Angular velocity—pulley rotation
A pulley belt 10.0 ft long takes 2.00 s to make one complete revolution. The radius of the pulley is 6.00 in. What is the angular velocity (in revolutions per minute) of a point on the rim of the pulley? See Fig. 8.39.
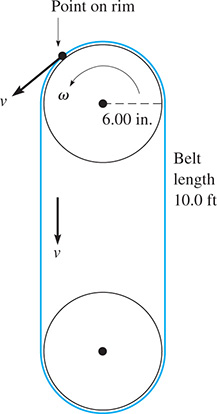
Fig. 8.39
Because the linear velocity of a point on the rim of the pulley is the same as the velocity of the belt, The radius of the pulley is and we can find by substituting into Eq. (8.11). This gives us
To convert this answer to revolutions per minute, we use the procedure described in Section 1.4:
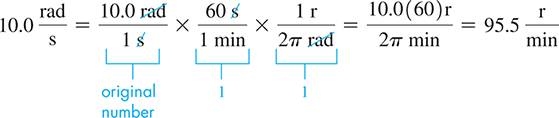
Many types of problems use radian measure. Following is one involving electric current.
EXAMPLE 7 Application to electric current
The current at any time in a certain alternating-current electric circuit is given by where I is the maximum current and t is the time in seconds. Given that find i for
Substituting, with the calculator in radian mode, we get
NOTE
[ is a pure number, and therefore is an angle in radians.]
EXERCISES 8.4
In Example 1, change to
In Example 3(a), change 17.5% to 18.5%.
In Example 4, change 90.0 m to 115 m.
In Example 6, change 2.00 s to 2.50 s.
In traveling three-fourths of the way around a traffic circle a car travels 0.203 mi. What is the radius of the traffic circle? See Fig. 8.40.
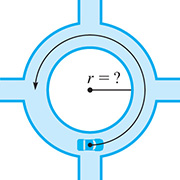
Fig. 8.40
 The latitude of Miami is N, and the latitude of the north end of the Panama Canal is N. Both are at a longitude of W. What is the distance between Miami and the Canal? Explain how the angle used in the solution is found. The radius of the Earth is 3960 mi.
The latitude of Miami is N, and the latitude of the north end of the Panama Canal is N. Both are at a longitude of W. What is the distance between Miami and the Canal? Explain how the angle used in the solution is found. The radius of the Earth is 3960 mi.The central angle corresponding to the part of a belt making contact with the larger pulley in Fig. 8.41 is . Find the length of the belt in contact with the pulley if its radius is 4.50 in.

Fig. 8.41
A pizza is cut into eight equal pieces, the area of each being What was the diameter of the original pizza?
When between 12:00 noon and 1:00 p.m. are the minute and hour hands of a clock apart?
A cam is in the shape of a circular sector, as shown in Fig. 8.42. What is the perimeter of the cam?
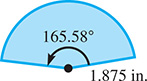
Fig. 8.42
A lawn sprinkler can water up to a distance of 65.0 ft. It turns through an angle of . What area can it water?
A spotlight beam sweeps through a horizontal angle of . If the range of the spotlight is 250 ft, what area can it cover?
If a car makes a U-turn in 6.0 s, what is its average angular velocity in the turn, expressed in rad/s?
A ceiling fan has blades 61.0 cm long. What is the linear velocity of the tip of a blade when the fan is rotating at 8.50 r/s?
What is the floor area of the hallway shown in Fig. 8.43? The outside and inside of the hallway are circular arcs.
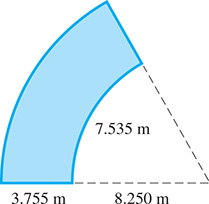
Fig. 8.43
The arm of a car windshield wiper is 12.75 in. long and is attached at the middle of a 15.00-in. blade. (Assume that the arm and blade are in line.) What area of the windshield is cleaned by the wiper if it swings through arcs?
Part of a railroad track follows a circular arc with a central angle of . If the radius of the arc of the inner rail is 93.67 ft and the rails are 4.71 ft apart, how much longer is the outer rail than the inner rail?
A wrecking ball is dropped as shown in Fig. 8.44. Its velocity at the bottom of its swing is where g is the acceleration due to gravity. What is its angular velocity at the bottom if and

Fig. 8.44
Part of a security fence is built 2.50 m from a cylindrical storage tank 11.2 m in diameter. What is the area between the tank and this part of the fence if the central angle of the fence is ? See Fig. 8.45.

Fig. 8.45
Through what angle does the drum in Fig. 8.46 turn in order to lower the crate 18.5 ft?

Fig. 8.46
A section of road follows a circular arc with a central angle of . The radius of the inside of the curve is 285.0 m, and the road is 15.2 m wide. What is the volume of the concrete in the road if it is 0.305 m thick?
The propeller of the motor on a motorboat is rotating at 130 rad/s. What is the linear velocity of a point on the tip of a blade if it is 22.5 cm long?
A storm causes a pilot to follow a circular-arc route, with a central angle of , from city A to city B rather than the straight-line route of 185.0 km. How much farther does the plane fly due to the storm? (Hint: First find the radius of the circle.)
An interstate route exit is a circular arc 330 m long with a central angle of . What is the radius of curvature of the exit?
The paddles of a riverboat have a radius of 8.50 ft and revolve at 20.0 r/min. What is the speed of a tip of one of the paddles?
The sweep second hand of a watch is 15.0 mm long. What is the linear velocity of the tip?
A DVD has a diameter of 4.75 in. and rotates at 360.0 r/min. What is the linear velocity of a point on the outer edge?
The Singapore Flyer is a Ferris wheel that has 28 air-conditioned capsules, each able to hold 28 people. It is 165 m high, with a 150-m-diameter wheel, and makes one revolution in 37 min. Find the speed (in cm/s) of a capsule.
GPS satellites orbit the Earth twice per day with an orbital radius of 26,600 km. What is the linear velocity (in km/s) of these satellites?
Assume that the Earth rotates around the sun in a circular orbit of radius 93,000,000 mi. (which is approximately correct). What is the Earth’s linear velocity (in mi/h)?
The sprocket assembly for a 28.0-in. bike is shown in Fig. 8.47. How fast (in r/min) does the rider have to pedal in order to go 15.0 mi/h on level ground?
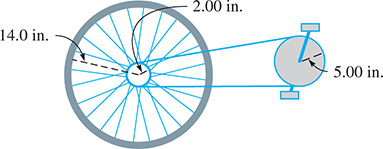
Fig. 8.47
The flywheel of a car engine is 0.36 m in diameter. If it is revolving at 750 r/min, through what distance does a point on the rim move in 2.00 s?
Two streets meet at an angle of . What is the length of the piece of curved curbing at the intersection if it is constructed along the arc of a circle 15.0 ft in radius? See Fig. 8.48.
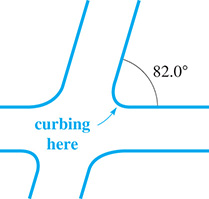
Fig. 8.48
An ammeter needle is deflected by a current of 0.2500 A. The needle is 3.750 in. long, and a circular scale is used. How long is the scale for a maximum current of 1.500 A?
A drill bit in diameter rotates at 1200 r/min. What is the linear velocity of a point on its circumference?
A helicopter blade is 2.75 m long and is rotating at 420 r/min. What is the linear velocity of the tip of the blade?
Most DVD players use constant linear velocity. This means that the angular velocity of the disk continually changes, but the linear velocity of the point being read by the laser remains the same. If a DVD rotates at 1590 r/min for a point 2.25 cm from the center, find the number of revolutions per minute for a point 5.51 cm from the center.
A jet is traveling westward with the sun directly overhead (the jet is on a line between the sun and the center of the Earth). How fast must the jet fly in order to keep the sun directly overhead? (Assume that the Earth’s radius is 3960 mi, the altitude of the jet is low, and the Earth rotates about its axis once in 24.0 h.)
A 1500-kW wind turbine (windmill) rotates at 40.0 r/min. What is the linear velocity of a point on the end of a blade, if the blade is 35 ft long (from the center of rotation)?
What is the linear velocity of a point in Charleston, South Carolina, which is at a latitude of The radius of the Earth is 3960 mi.
Through what total angle does the drive shaft of a car rotate in 1 s when the tachometer reads 2400 r/min?
A baseball field is designed such that the outfield fence is along the arc of a circle with its center at second base. If the radius of the circle is 280 ft, what is the playing area of the field? See Fig. 8.49.
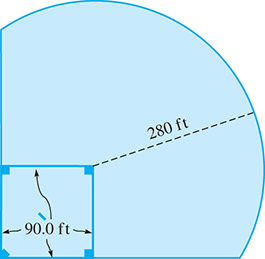
Fig. 8.49
The turbine fan blade of a turbojet engine is 1.2 m in diameter and rotates at 250 r/s. How fast is the tip of a blade moving?
A patio is in the shape of a circular sector with a central angle of . It is enclosed by a railing of which the circular part is 11.6 m long. What is the area of the patio?
An oil storage tank 4.25 m long has a flat bottom as shown in Fig. 8.50. The radius of the circular part is 1.10 m. What volume of oil does the tank hold?
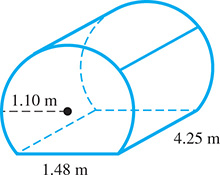
Fig. 8.50
Two equal beams of light illuminate the area shown in Fig. 8.51. What area is lit by both beams?
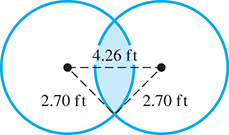
Fig. 8.51
 Use a calculator (in radian mode) to evaluate the ratios and for 0.01, 0.001, and 0.0001. From these values, explain why it is possible to say that(8.12)
Use a calculator (in radian mode) to evaluate the ratios and for 0.01, 0.001, and 0.0001. From these values, explain why it is possible to say that(8.12)approximately for very small angles measured in radians.
Using Eq. (8.12), evaluate . Compare with a calculator value.
An astronomer observes that a star 12.5 light-years away moves through an angle of in 1 year. Assuming it moved in a straight line perpendicular to the initial line of observation, how many miles did the star move? Use Eq. (8.12).
In calculating a back line of a lot, a surveyor discovers an error of in an angle measurement. If the lot is 136.0 m deep, by how much is the back-line calculation in error? See Fig. 8.52. Use Eq. (8.12).

Fig. 8.52
Answers to Practice Exercises
14,300 ft
