Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

6.1 Factoring: Greatest Common Factor and Difference of Squares

Factoring • Factoring Out the GCF • Factoring Difference of Two Squares • Prime Factors • Factoring Completely • Factoring by Grouping

When an algebraic expression is written as the product of two or more quantities, each of these quantities is called a factor of the expression. In practice, we often have an expression and we need to find its factors. Finding these factors, which is essentially reversing the process of multiplication, is called factoring. Factoring is needed in many technical applications that require us to solve higher-degree equations, perform operations on algebraic fractions, or solve certain literal equations.

Since factoring is the reversal of multiplying, it is important that we understand certain types of special products. Each special product, when used in reverse, gives us a method for factoring. The first three sections of this chapter are devoted to discussing different techniques that can be used to factor expressions. In this section, we discuss the first two of these techniques: factoring out the greatest common factor and factoring the difference of squares.

FACTORING OUT THE GREATEST COMMON FACTOR (GCF)

From the distributive law, we know that $a (x + y) = a x + a y$ $a (x + y) = a x + a y$ . When written in reverse, this becomes

a x + a y = a (x + y)

$a x + a y = a (x + y)$ (6.1)

Equation (6.1) provides us with a technique of factoring called factoring out the greatest common factor (or GCF, for short). In this case, a is the GCF and it has been factored out of the expression.

To factor out the GCF, we first find the greatest monomial that is common to each term of the expression. This is the GCF. We then use Eq. (6.1) to write the expression as the product of the GCF and the remaining expression. Although we will be discussing several other factoring techniques in this chapter, factoring out the GCF is always the first step in factoring. The following examples illustrate this method.

EXAMPLE 1 Factoring out the GCF

In factoring $6 x - 2 y,$ $6 x - 2 y,$ we note each term contains a factor of 2:

6 x minus 2 y = 2 times left parenthesis 3 x right parenthesis minus 2 y = 2 left parenthesis 3 x minus y right parenthesis.

Here, 2 is the greatest common factor, and $2 (3 x - y)$ $2 (3 x - y)$ is the required factored form of $6 x - 2 y$ $6 x - 2 y$ .

NOTE

[We check the result by multiplication.] In this case,

2 (3 x - y) = 6 x - 2 y

$2 (3 x - y) = 6 x - 2 y$

Since the result of the multiplication gives the original expression, the factored form is correct.

In Example 1, we determined the greatest common factor of 2 by inspection. This is normally the way in which it is found. Once the GCF has been found, the other factor can be determined by dividing the original expression by the GCF.

The next example illustrates the case where the GCF is the same as one of the terms, and special care must be taken to complete the factoring correctly.

EXAMPLE 2 Greatest common factor same as term

Factor: $4 a x^{2} + 2 a x$ $4 a x^{2} + 2 a x$ .

The numerical factor 2 and the literal factors a and x are common to each term. Therefore, the greatest common factor of $4 a x^{2} + 2 a x$ $4 a x^{2} + 2 a x$ is 2ax. This means that

4 a x^{2} + 2 a x = 2 a x (2 x) + 2 a x (1) = 2 a x (2 x + 1)

$4 a x^{2} + 2 a x = 2 a x (2 x) + 2 a x (1) = 2 a x (2 x + 1)$

Note the presence of the 1 in the factored form. When we divide $4 a x^{2} + 2 a x$ $4 a x^{2} + 2 a x$ by 2ax, we get

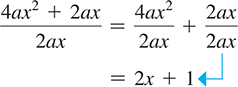
Start fraction 4 a x squared + 2 a x over 2 a x end fraction = start fraction 4 a x squared over 2 a x end fraction + start fraction 2 a x over 2 a x end fraction = 2 x + 1.

CAUTION

Note that in Example 2, 2ax divided by 2ax is 1 and does not simply cancel out leaving nothing. In cases like this, where the GCF is the same as one of the terms, it is a common error to omit the 1. However, we must include the 1. Without it, when the factored form is multiplied out, we would not obtain the original expression.

Usually, the division shown in Example 2 is done mentally. However, we show it here to emphasize the actual operation that is being performed when we factor out a GCF.

EXAMPLE 3 Greatest common factor by inspection

Factor: $6 a^{5} x^{2} - 9 a^{3} x^{3} + 3 a^{3} x^{2}$ $6 a^{5} x^{2} - 9 a^{3} x^{3} + 3 a^{3} x^{2}$ .

After inspecting each term, we determine that each contains a factor of 3, $a^{3},$ $a^{3},$ and $x^{2}$ $x^{2}$ . Thus, the greatest common factor is $3 a^{3} x^{2}$ $3 a^{3} x^{2}$ . This means that

6 a^{5} x^{2} - 9 a^{3} x^{3} + 3 a^{3} x^{2} = 3 a^{3} x^{2} (2 a^{2} - 3 x + 1)

$6 a^{5} x^{2} - 9 a^{3} x^{3} + 3 a^{3} x^{2} = 3 a^{3} x^{2} (2 a^{2} - 3 x + 1)$

When factoring, it is important to factor out the greatest common factor, not just any common factor. Factoring out something other than the GCF will lead to an expression that is not factored completely. To be factored completely, the factors must be prime, meaning they contain no factor other than $\pm 1$ $\pm 1$ and $\pm$ $\pm$ itself. The following example illustrates this point.

EXAMPLE 4 Factoring completely

If we factor the common factor of 2 out of the expression $12 x + 6 x^{2},$ $12 x + 6 x^{2},$ we get $12 x + 6 x^{2} = 2 (6 x + 3 x^{2})$ $12 x + 6 x^{2} = 2 (6 x + 3 x^{2})$ .

However, this is not factored completely. The factor $6 x + 3 x^{2}$ $6 x + 3 x^{2}$ is not prime because it may be further factored as $6 x + 3 x^{2} = 3 x (2 + x)$ $6 x + 3 x^{2} = 3 x (2 + x)$ .

If we instead factor out the greatest common factor 6x, we get $12 x + 6 x^{2} = 6 x (2 + x)$ $12 x + 6 x^{2} = 6 x (2 + x)$ .

This is now factored completely since the factor $2 + x$ $2 + x$ is prime.

In these examples, note that factoring an expression does not actually change the expression, although it does change the form of the expression. In equating the expression to its factored form, we write an identity.

It is often necessary to use factoring when solving an equation. This is illustrated in the following example.

EXAMPLE 5 Using factoring to solve a literal equation—FM reception

An equation used in the analysis of FM reception is $R_{F} = α (2 R_{A} + R_{F})$ $R_{F} = α (2 R_{A} + R_{F})$ . Solve for $R_{F}$ $R_{F}$ .

The steps in the solution are as follows:

\begin{aligned} R_{F} & = & α (2 R_{A} + R_{F}) & original equation \\ R_{F} & = & 2 α R_{A} + α R_{F} & use distributive law \\ R_{F} - α R_{F} & = & 2 α R_{A} & subtract α R_{F} from both sides \\ R_{F} (1 - α) & = & 2 α R_{A} & factor out R_{F} on left \\ R_{F} & = & \frac{2 α R_{A}}{1 - α} & divide both sides by 1 - α \end{aligned}

$\begin{aligned} R_{F} & = & α (2 R_{A} + R_{F}) & original equation \\ R_{F} & = & 2 α R_{A} + α R_{F} & use distributive law \\ R_{F} - α R_{F} & = & 2 α R_{A} & subtract α R_{F} from both sides \\ R_{F} (1 - α) & = & 2 α R_{A} & factor out R_{F} on left \\ R_{F} & = & \frac{2 α R_{A}}{1 - α} & divide both sides by 1 - α \end{aligned}$

We see that we collected both terms containing $R_{F}$ $R_{F}$ on the left so that we could factor and thereby solve for $R_{F}$ $R_{F}$ .

FACTORING THE DIFFERENCE OF TWO SQUARES

From Section 1.8, we know that in order to multiply two binomials, we multiply each term of the first binomial by each term of the second. When we apply this procedure to the special product $(a + b) (a - b),$ $(a + b) (a - b),$ we get $(a + b) (a - b) = a^{2} - a b + a b - b^{2}$ $(a + b) (a - b) = a^{2} - a b + a b - b^{2}$ . Since the two terms in the middle add up to zero, this simplifies to the following:

(a + b) (a - b) = a^{2} - b^{2}

$(a + b) (a - b) = a^{2} - b^{2}$

(6.2)

We can use Eq. (6.2) to find this type of special product directly, as shown in the following example:

EXAMPLE 6 Finding the product (a + b)(a − b)

$(2 x + 5) (2 x - 5) = {(2 x)}^{2} - 5^{2} = 4 x^{2} - 25 Eq . (6.2)$ $(2 x + 5) (2 x - 5) = {(2 x)}^{2} - 5^{2} = 4 x^{2} - 25 Eq . (6.2)$
To find the product $F a (L - a) (L + a),$ $F a (L - a) (L + a),$ which arises from analyzing forces on a beam, we have

$\begin{aligned} F a (L - a) (L + a) & = & F a (L^{2} - a^{2}) & Eq . (6.2) \\ = & F a L^{2} - F a^{3} & distributive property \end{aligned}$ $\begin{aligned} F a (L - a) (L + a) & = & F a (L^{2} - a^{2}) & Eq . (6.2) \\ = & F a L^{2} - F a^{3} & distributive property \end{aligned}$

An important consequence of Eq. (6.2) is that, when written in reverse, it gives us a method of factoring called factoring the difference of two squares.

a^{2} - b^{2} = (a + b) (a - b)

$a^{2} - b^{2} = (a + b) (a - b)$

(6.3)

Equation (6.3) can be used to factor the difference between two perfect squares as shown in the following examples.

EXAMPLE 7 Factoring difference of two squares

In factoring $x^{2} - 16,$ $x^{2} - 16,$ note that $x^{2}$ $x^{2}$ is the square of x and 16 is the square of 4. Therefore,

x squared minus 16 = x squared minus 4 squared = left parenthesis x + 4 right parenthesis left parenthesis x minus 4 right parenthesis. Where + is the sum and minus is the difference.

EXAMPLE 8 Factoring difference of two squares

Because $4 x^{2}$ $4 x^{2}$ is the square of 2x and 9 is the square of 3, we may factor $4 x^{2} - 9$ $4 x^{2} - 9$ as

$4 x^{2} - 9 = {(2 x)}^{2} - 3^{2} = (2 x + 3) (2 x - 3)$ $4 x^{2} - 9 = {(2 x)}^{2} - 3^{2} = (2 x + 3) (2 x - 3)$
In the same way,

$\begin{aligned} {(y - 3)}^{2} - 16 x^{4} & = & [(y - 3) + 4 x^{2}] [(y - 3) - 4 x^{2}] \\ = & (y - 3 + 4 x^{2}) (y - 3 - 4 x^{2}) \end{aligned}$ $\begin{aligned} {(y - 3)}^{2} - 16 x^{4} & = & [(y - 3) + 4 x^{2}] [(y - 3) - 4 x^{2}] \\ = & (y - 3 + 4 x^{2}) (y - 3 - 4 x^{2}) \end{aligned}$

where we note that $16 x^{4} = {(4 x^{2})}^{2}$ $16 x^{4} = {(4 x^{2})}^{2}$ .

FACTORING COMPLETELY

NOTE

[However, we must be careful to see if the other factor can itself be factored.]

As noted before, the greatest common factor should be factored out first. It is possible, for example, that the other factor is the difference of squares.

CAUTION

This means that complete factoring often requires more than one step. Be sure to include only prime factors in the final result.

EXAMPLE 9 Factoring completely

In factoring $20 x^{2} - 45,$ $20 x^{2} - 45,$ note a common factor of 5 in each term. Therefore, $20 x^{2} - 45 = 5 (4 x^{2} - 9)$ $20 x^{2} - 45 = 5 (4 x^{2} - 9)$ . However, the factor $4 x^{2} - 9$ $4 x^{2} - 9$ itself is the difference of squares. Therefore, $20 x^{2} - 45$ $20 x^{2} - 45$ is completely factored as

.1-2 Full Alternative Text
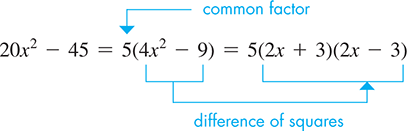
In factoring $x^{4} - y^{4},$ $x^{4} - y^{4},$ note that we have the difference of two squares. Therefore, $x^{4} - y^{4} = (x^{2} + y^{2}) (x^{2} - y^{2})$ $x^{4} - y^{4} = (x^{2} + y^{2}) (x^{2} - y^{2})$ . However, the factor $x^{2} - y^{2}$ $x^{2} - y^{2}$ is also the difference of squares. This means that

$x^{4} - y^{4} = (x^{2} + y^{2}) (x^{2} - y^{2}) = (x^{2} + y^{2}) (x + y) (x - y)$ $x^{4} - y^{4} = (x^{2} + y^{2}) (x^{2} - y^{2}) = (x^{2} + y^{2}) (x + y) (x - y)$
In analyzing the energy collected by different circular solar cells, the expression $45 R^{2} - 20 r^{2}$ $45 R^{2} - 20 r^{2}$ arises. In factoring this expression, we note the factor 5 in each term. Therefore, $45 R^{2} - 20 r^{2} = 5 (9 R^{2} - 4 r^{2})$ $45 R^{2} - 20 r^{2} = 5 (9 R^{2} - 4 r^{2})$ . However, $9 R^{2} - 4 r^{2}$ $9 R^{2} - 4 r^{2}$ is the difference of squares. Therefore, factoring the original expression, we have

$45 R^{2} - 20 r^{2} = 5 (9 R^{2} - 4 r^{2}) = 5 (3 R - 2 r) (3 R + 2 r)$ $45 R^{2} - 20 r^{2} = 5 (9 R^{2} - 4 r^{2}) = 5 (3 R - 2 r) (3 R + 2 r)$

CAUTION

In Example 9(b), the factor $x^{2} + y^{2}$ $x^{2} + y^{2}$ is prime. It is not equal to ${(x + y)}^{2}$ ${(x + y)}^{2}$ since ${(x + y)}^{2} = (x + y) (x + y) = x^{2} + 2 x y + y^{2}$ ${(x + y)}^{2} = (x + y) (x + y) = x^{2} + 2 x y + y^{2}$ .

FACTORING BY GROUPING

Terms in an expression can sometimes be grouped and then factored by methods of this section. The following example illustrates this method of factoring by grouping. In the next section, we discuss another type of expression that can be factored by grouping.

EXAMPLE 10 Factoring by grouping

Factor: $2 x - 2 y + a x - a y$ $2 x - 2 y + a x - a y$ .

We see that there is no common factor to all four terms, but that each of the first two terms contains a factor of 2, and each of the third and fourth terms contains a factor of a. Grouping terms this way and then factoring each group, we have

\begin{array}{l} 2 x - 2 y + a x - a y = (2 x - 2 y) + (a x - a y) \\ = 2 (x - y) + a (x - y) now note the common factor of (x - y) \\ = (x - y) (2 + a) \end{array}

$\begin{array}{l} 2 x - 2 y + a x - a y = (2 x - 2 y) + (a x - a y) \\ = 2 (x - y) + a (x - y) now note the common factor of (x - y) \\ = (x - y) (2 + a) \end{array}$

EXERCISES 6.1

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the indicated problems.

In Example 2, change the $+$ $+$ sign to $-$ $-$ and then factor.
In Example 2, set the given expression equal to B and then solve for a.
In Example 9(a), change the coefficient of the first term from 20 to 5 and then factor.
In Example 10, change both $-$ $-$ signs to $+$ $+$ and then factor.

In Exercises 5–8, find the indicated special products directly by inspection.

$(T + 6) (T - 6)$ $(T + 6) (T - 6)$
$(s + 5 t) (s - 5 t)$ $(s + 5 t) (s - 5 t)$
$(4 x - 5 y) (4 x + 5 y)$ $(4 x - 5 y) (4 x + 5 y)$
$(3 v - 7 y) (3 v + 7 y)$ $(3 v - 7 y) (3 v + 7 y)$

In Exercises 9–48, factor the given expressions completely.

$7 x + 7 y$ $7 x + 7 y$
$3 a - 3 b$ $3 a - 3 b$
$5 a - 5$ $5 a - 5$
$2 x^{2} + 2$ $2 x^{2} + 2$
$3 x^{2} - 9 x$ $3 x^{2} - 9 x$
$20 s + 4 s^{2}$ $20 s + 4 s^{2}$
$7 b^{2} h - 28 b$ $7 b^{2} h - 28 b$
$5 a^{2} - 20 a x$ $5 a^{2} - 20 a x$
$72 n^{3} + 24 n$ $72 n^{3} + 24 n$
$90 p^{3} - 15 p^{2}$ $90 p^{3} - 15 p^{2}$
$2 x + 4 y - 8 z$ $2 x + 4 y - 8 z$
$23 a - 46 b + 69 c$ $23 a - 46 b + 69 c$
$3 a b^{2} - 6 a b + 12 a b^{3}$ $3 a b^{2} - 6 a b + 12 a b^{3}$
$4 p q - 14 q^{2} - 16 p q^{2}$ $4 p q - 14 q^{2} - 16 p q^{2}$
$12 p q^{2} - 8 p q - 28 p q^{3}$ $12 p q^{2} - 8 p q - 28 p q^{3}$
$27 a^{2} b - 24 a b - 9 a$ $27 a^{2} b - 24 a b - 9 a$
$2 a^{2} - 2 b^{2} + 4 c^{2} - 6 d^{2}$ $2 a^{2} - 2 b^{2} + 4 c^{2} - 6 d^{2}$
$5 a + 10 a x - 5 a y - 20 a z$ $5 a + 10 a x - 5 a y - 20 a z$
$x^{2} - 9$ $x^{2} - 9$
$r^{2} - 25$ $r^{2} - 25$
$100 - 4 A^{2}$ $100 - 4 A^{2}$
$49 - Z^{4}$ $49 - Z^{4}$
$36 a^{4} + 1$ $36 a^{4} + 1$
$324 z^{2} + 4$ $324 z^{2} + 4$
$162 s^{2} - 50 t^{2}$ $162 s^{2} - 50 t^{2}$
$36 s^{2} - 121 t^{4}$ $36 s^{2} - 121 t^{4}$
$144 n^{2} - 169 p^{4}$ $144 n^{2} - 169 p^{4}$
$36 a^{2} b^{2} + 169 c^{2}$ $36 a^{2} b^{2} + 169 c^{2}$
${(x + y)}^{2} - 9$ ${(x + y)}^{2} - 9$
${(a - b)}^{2} - 1$ ${(a - b)}^{2} - 1$
$8 - 2 x^{2}$ $8 - 2 x^{2}$
$5 a^{4} - 125 a^{2}$ $5 a^{4} - 125 a^{2}$
$300 x^{2} - 2700 z^{2}$ $300 x^{2} - 2700 z^{2}$
$28 x^{2} - 700 y^{2}$ $28 x^{2} - 700 y^{2}$
$2 {(I - 3)}^{2} - 8$ $2 {(I - 3)}^{2} - 8$
$a {(x + 2)}^{2} - a y^{2}$ $a {(x + 2)}^{2} - a y^{2}$
$x^{4} - 16$ $x^{4} - 16$
$81 - y^{4}$ $81 - y^{4}$
$x^{10} - x^{2}$ $x^{10} - x^{2}$
$2 x^{4} - 8 y^{4}$ $2 x^{4} - 8 y^{4}$

In Exercises 49–54, solve for the indicated variable.

$2 a - b = a b + 3,$ $2 a - b = a b + 3,$ for a
$n (x + 1) = 5 - x,$ $n (x + 1) = 5 - x,$ for x
$3 - 2 s = 2 (3 - s t),$ $3 - 2 s = 2 (3 - s t),$ for s
$k (2 - y) = y (2 k - 1),$ $k (2 - y) = y (2 k - 1),$ for y
$(x + 2 k) (x - 2) = x^{2} + 3 x - 4 k,$ $(x + 2 k) (x - 2) = x^{2} + 3 x - 4 k,$ for k
$(2 x - 3 k) (x + 1) = 2 x^{2} - x - 3,$ $(2 x - 3 k) (x + 1) = 2 x^{2} - x - 3,$ for k

In Exercises 55–62, factor the given expressions by grouping as illustrated in Example 10.

$3 x - 3 y + b x - b y$ $3 x - 3 y + b x - b y$
$a m + a n + c n + c m$ $a m + a n + c n + c m$
$a^{2} + a x - a b - b x$ $a^{2} + a x - a b - b x$
$2 y - y^{2} - 6 y^{4} + 12 y^{3}$ $2 y - y^{2} - 6 y^{4} + 12 y^{3}$
$x^{3} + 3 x^{2} - 4 x - 12$ $x^{3} + 3 x^{2} - 4 x - 12$
$S^{3} - 5 S^{2} - S + 5$ $S^{3} - 5 S^{2} - S + 5$
$x^{2} - y^{2} + x - y$ $x^{2} - y^{2} + x - y$
$4 p^{2} - q^{2} + 2 p + q$ $4 p^{2} - q^{2} + 2 p + q$

In Exercises 63 and 64, evaluate the given expressions by using factoring. The results may be checked with a calculator.

$\frac{8^{9} - 8^{8}}{7}$ $\frac{8^{9} - 8^{8}}{7}$
$\frac{5^{9} - 5^{7}}{7^{2} - 5^{2}}$ $\frac{5^{9} - 5^{7}}{7^{2} - 5^{2}}$

In Exercises 65 and 66, give the required explanations.

Factor $n^{2} + n,$ $n^{2} + n,$ and then explain why it represents a positive even integer if n is a positive integer.
Factor $n^{3} - n,$ $n^{3} - n,$ and then explain why it represents a multiple of 6 if n is an integer greater than 1.

In Exercises 67–76, factor the expressions completely. In Exercises 73 and 74, it is necessary to set up the proper expression. Each expression comes from the technical area indicated.

$2 Q^{2} + 2$ $2 Q^{2} + 2$ (fire science)
$4 d^{2} D^{2} - 4 d^{3} D - d^{4}$ $4 d^{2} D^{2} - 4 d^{3} D - d^{4}$ (machine design)
$81 s - s^{3}$ $81 s - s^{3}$ (rocket path)
$12 (4 - x^{2}) - 2 x (4 - x^{2}) - {(4 - x^{2})}^{2}$ $12 (4 - x^{2}) - 2 x (4 - x^{2}) - {(4 - x^{2})}^{2}$ (container design)
$r R^{2} - r^{3}$ $r R^{2} - r^{3}$ (pipeline flow)
$p_{1} R^{2} - p_{1} r^{2} - p_{2} R^{2} + p_{2} r^{2}$ $p_{1} R^{2} - p_{1} r^{2} - p_{2} R^{2} + p_{2} r^{2}$ (fluid flow)
A square as large as possible is cut from a circular metal plate of radius r. Express in factored form the area of the metal pieces that are left.
A pipe of outside diameter d is inserted into a pipe of inside radius r. Express in factored form the cross-sectional area within the larger pipe that is outside the smaller pipe.
A spherical float has a volume of air within it of radius $r_{1},$ $r_{1},$ and the outer radius of the float is $r_{2}$ $r_{2}$ . Express in factored form the difference in areas of the outer surface and the inner surface.
The kinetic energy of an object of mass m traveling at velocity v is given by $\frac{1}{2} {m v}^{2}$ $\frac{1}{2} {m v}^{2}$ . Suppose a car of mass $m_{0}$ $m_{0}$ equipped with a crash-avoidance system automatically applies the brakes to avoid a collision and slows from a velocity of $v_{1}$ $v_{1}$ to a velocity of $v_{2}$ $v_{2}$ . Find an expression, in factored form, for the difference between the original and final kinetic energy.

In Exercises 77–82, solve for the indicated variable. Each equation comes from the technical area indicated.

$i_{1} R_{1} = (i_{2} - i_{1}) R_{2},$ $i_{1} R_{1} = (i_{2} - i_{1}) R_{2},$ for $i_{1}$ $i_{1}$ (electricity: ammeter)
$n V + n_{1} v = n_{1} V,$ $n V + n_{1} v = n_{1} V,$ for $n_{1}$ $n_{1}$ (acoustics)
$3 B Y + 5 Y = 9 B S,$ $3 B Y + 5 Y = 9 B S,$ for B (physics: elasticity)
$S q + S p = S p q + p,$ $S q + S p = S p q + p,$ for q (computer design)
$E R = A t T_{0} - A t T_{1},$ $E R = A t T_{0} - A t T_{1},$ for t (energy conservation)
$R = k T_{2}^{4} - k T_{1}^{4},$ $R = k T_{2}^{4} - k T_{1}^{4},$ for k (factor resulting denominator) (radiation)

Answers to Practice Exercises

$3 c x (x^{2} - 3)$ $3 c x (x^{2} - 3)$
$3 c x (3 x^{2} - 1)$ $3 c x (3 x^{2} - 1)$
$(3 c - 8) (3 c + 8)$ $(3 c - 8) (3 c + 8)$
$2 (3 c - 8) (3 c + 8)$ $2 (3 c - 8) (3 c + 8)$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 6.1 Factoring: Greatest Common Factor and&#160;Difference&#160;of&#160;Squares Factoring: Greatest Common Factor and Difference of Squares

Create new playlist

Sign In

Sign Up

Table of Contents for
6.1 Factoring: Greatest Common Factor and Difference of Squares Factoring: Greatest Common Factor and Difference of Squares