Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

7.1 Quadratic Equations; Solution by Factoring

General Quadratic Equation • Solutions of a Quadratic Equation • Solving a Quadratic Equation by Factoring • Equations with Fractions

Given that a, b, and c are constants $(a \neq 0),$ $(a \neq 0),$ the equation

a x^{2} + b x + c = 0

$a x^{2} + b x + c = 0$ (7.1)

is called the general quadratic equation in x. The left side of Eq. (7.1) is a polynomial function of degree 2. This function, $f (x) = a x^{2} + b x + c,$ $f (x) = a x^{2} + b x + c,$ is known as the quadratic function. Any equation that can be simplified and then written in the form of Eq. (7.1) is a quadratic equation in one unknown.

Among the applications of quadratic equations and functions are the following examples: In finding the flight time t of a projectile, the equation $s_{0} + v_{0} t - 16 t^{2} = 0$ $s_{0} + v_{0} t - 16 t^{2} = 0$ occurs; in analyzing the electric current i in a circuit, the function $f (i) = E i - R i^{2}$ $f (i) = E i - R i^{2}$ is found; and in determining the forces at a distance x along a beam, the function $f (x) = a x^{2} + b L x + c L^{2}$ $f (x) = a x^{2} + b L x + c L^{2}$ is used.

NOTE

[Because it is the $x^{2} -term$ $x^{2} -term$ in Eq. (7.1) that distinguishes the quadratic equation from other types of equations, the equation is not quadratic if $a = 0.$ $a = 0.$ However, either b or c (or both) may be zero, and the equation is still quadratic.]

No power of x higher than the second may be present in a quadratic equation. Also, we should be able to properly identify a quadratic equation even when it does not initially appear in the form of Eq. (7.1). The following two examples illustrate how we may recognize quadratic equations.

EXAMPLE 1 Examples of quadratic equations

The following are quadratic equations.

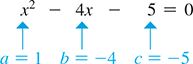x squared minus 4 x minus 5 = 0. The x squared coefficient value of a is 1, 4 x coefficient value of b is negative 4, and 5 constant value of c is negative 5.

3 x squared minus 6 = 0. The 3 x squared coefficient value of a is 3, and 6 constant value of c is negative 6.

EXAMPLE 2 Examples of equations not quadratic

The following are not quadratic equations.

\begin{array}{rcl} b x - 6 & = & 0 & There is no x^{2} -term . \\ x^{3} - x^{2} - 5 & = & 0 & There should be no term of degree higher than 2. Thus, there \\ can be no x^{3} -term in a quadratic equation . \\ x^{2} + x - 7 & = & x^{2} & When terms are collected, there will be no x^{2} -term . \end{array}

$\begin{array}{rcl} b x - 6 & = & 0 & There is no x^{2} -term . \\ x^{3} - x^{2} - 5 & = & 0 & There should be no term of degree higher than 2. Thus, there \\ can be no x^{3} -term in a quadratic equation . \\ x^{2} + x - 7 & = & x^{2} & When terms are collected, there will be no x^{2} -term . \end{array}$

SOLUTIONS OF A QUADRATIC EQUATION

Recall that the solution of an equation consists of all numbers (roots), which, when substituted in the equation, give equality. There are two roots for a quadratic equation. At times, these roots are equal (see Example 3), so only one number is actually a solution. Also, the roots can contain imaginary numbers. If this happens, all we wish to do at this point is to recognize that there are no real roots.

EXAMPLE 3 Solutions (roots) of a quadratic equation

The quadratic equation $3 x^{2} - 7 x + 2 = 0$ $3 x^{2} - 7 x + 2 = 0$ has roots $x = 1/3$ $x = 1/3$ and $x = 2.$ $x = 2.$ This is seen by substituting these numbers in the equation.

$\begin{array}{rcl} 3 {(\frac{1}{3})}^{2} - 7 (\frac{1}{3}) + 2 & = & 3 (\frac{1}{9}) - \frac{7}{3} + 2 = \frac{1}{3} - \frac{7}{3} + 2 = \frac{0}{3} = 0 \\ 3 {(2)}^{2} - 7 (2) + 2 & = & 3 (4) - 14 + 2 = 14 - 14 = 0 \end{array}$ $\begin{array}{rcl} 3 {(\frac{1}{3})}^{2} - 7 (\frac{1}{3}) + 2 & = & 3 (\frac{1}{9}) - \frac{7}{3} + 2 = \frac{1}{3} - \frac{7}{3} + 2 = \frac{0}{3} = 0 \\ 3 {(2)}^{2} - 7 (2) + 2 & = & 3 (4) - 14 + 2 = 14 - 14 = 0 \end{array}$

Until the 1600s, most mathematicians did not accept negative, irrational, or imaginary roots of an equation. It was also generally accepted that an equation had only one root.
The quadratic equation $4 x^{2} - 4 x + 1 = 0$ $4 x^{2} - 4 x + 1 = 0$ has a double root (both roots are the same) of $x = 1/2.$ $x = 1/2.$ Showing that this number is a solution, we have

$4 {(\frac{1}{2})}^{2} - 4 (\frac{1}{2}) + 1 = 4 (\frac{1}{4}) - 2 + 1 = 1 - 2 + 1 = 0$ $4 {(\frac{1}{2})}^{2} - 4 (\frac{1}{2}) + 1 = 4 (\frac{1}{4}) - 2 + 1 = 1 - 2 + 1 = 0$
The quadratic equation $x^{2} + 9 = 0$ $x^{2} + 9 = 0$ has roots $x = \sqrt{- 9}$ $x = \sqrt{- 9}$ and $x = - \sqrt{- 9}$ $x = - \sqrt{- 9}$ . These are imaginary roots because they involve taking the square root of a negative number. There are no real roots.

SOLVING A QUADRATIC EQUATION BY FACTORING

We now describe a method for solving quadratic equations that relies on factoring.

NOTE

[Using the zero product rule, which states that a product is zero if and only if any of its factors is zero, we have the following steps in solving a quadratic equation.]

EXAMPLE 4 Solving quadratic equation by factoring

.1-2 Full Alternative Text

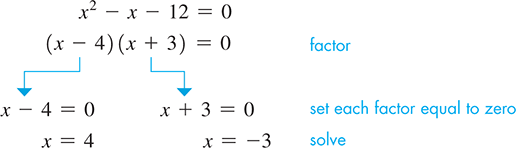
The roots are $x = 4$ $x = 4$ and $x = - 3.$ $x = - 3.$ We can check them in the original equation by substitution. Therefore,

\begin{array}{rclrcl} {(4)}^{2} - (4) - 12 & \overset{?}{=} & 0 & {(- 3)}^{2} - (- 3) - 12 & \overset{?}{=} & 0 \\ 0 & = & 0 & 0 & = & 0 \end{array}

$\begin{array}{rclrcl} {(4)}^{2} - (4) - 12 & \overset{?}{=} & 0 & {(- 3)}^{2} - (- 3) - 12 & \overset{?}{=} & 0 \\ 0 & = & 0 & 0 & = & 0 \end{array}$

Both roots satisfy the original equation.

EXAMPLE 5 First put equation in proper form

\begin{array}{rcll} x^{2} + 4 & = & 4 x & equation not in form of Eq . (7.1) \\ x^{2} - 4 x + 4 & = & 0 & subtract 4 x from both sides \\ {(x - 2)}^{2} & = & 0 & factor \\ x - 2 & = & 0, x = 2 & solve \end{array}

$\begin{array}{rcll} x^{2} + 4 & = & 4 x & equation not in form of Eq . (7.1) \\ x^{2} - 4 x + 4 & = & 0 & subtract 4 x from both sides \\ {(x - 2)}^{2} & = & 0 & factor \\ x - 2 & = & 0, x = 2 & solve \end{array}$

Because ${(x - 2)}^{2} = (x - 2) (x - 2),$ ${(x - 2)}^{2} = (x - 2) (x - 2),$ both factors are the same. This means there is a double root of $x = 2.$ $x = 2.$ Substitution shows that $x = 2$ $x = 2$ satisfies the original equation.

EXAMPLE 6 Quadratic equations with `b` = 0 or `c` = 0

In solving the equation $3 x^{2} - 12 = 0,$ $3 x^{2} - 12 = 0,$ we note that $b = 0$ $b = 0$ (there is no x-term). However, we can solve it by factoring. First we note the common factor of 3. Because it is a constant, we can first divide all terms by 3, and proceed with the solution.

.1-2 Full Alternative Text

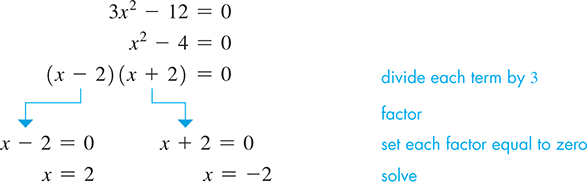
The roots 2 and $- 2$ $- 2$ check. We could also have first factored the 3 from each term, but the results would be the same since 3 is a constant, and the only two factors that can be set equal to zero are $x - 2$ $x - 2$ and $x + 2.$ $x + 2.$
In solving the equation $3 x^{2} - 12 x = 0,$ $3 x^{2} - 12 x = 0,$ we note that $c = 0$ $c = 0$ (there is no constant term). However, we can solve it by factoring. We note the factor of 3, and because 3 is a constant, we can divide each term by 3. Therefore,

NOTE

[We also note the common factor x, but because we are solving for x, we cannot divide each term by x. If we divide by x, we lose one of the two roots.]

$\begin{array}{rcl} 3 x^{2} - 12 x & = & 0 \\ x^{2} - 4 x & = & 0 & divide each term by 3, but not by x \\ x (x - 4) & = & 0 & factor \\ x & = & 0, 4 \end{array}$ $\begin{array}{rcl} 3 x^{2} - 12 x & = & 0 \\ x^{2} - 4 x & = & 0 & divide each term by 3, but not by x \\ x (x - 4) & = & 0 & factor \\ x & = & 0, 4 \end{array}$

These roots check. Again, if we had divided out the x, we would not have found the root $x = 0,$ $x = 0,$ and therefore our solution would be incomplete.

EXAMPLE 7 Quadratic equation—fire hose flow rate

For a certain fire hose, the pressure loss P (in $lb / {in.}^{2}$ $lb / {in.}^{2}$ per 100 ft of hose) is $P = 2 Q^{2} + Q,$ $P = 2 Q^{2} + Q,$ where Q is the flow rate (in 100 gal/min). Find Q for $P = 15 lb / {in.}^{2}$ $P = 15 lb / {in.}^{2}$ per 100 ft.

Substituting, we have the following equation and solution.

\begin{array}{rcll} 2 Q^{2} + Q & = & 15 \\ 2 Q^{2} + Q - 15 & = & 0 \\ (2 Q - 5) (Q + 3) & = & 0 \\ 2 Q - 5 & = & 0, & Q = 2.5100 gal / min \\ Q + 3 & = & 0, & Q = - 3100 gal / min not realistically possible \end{array}

$\begin{array}{rcll} 2 Q^{2} + Q & = & 15 \\ 2 Q^{2} + Q - 15 & = & 0 \\ (2 Q - 5) (Q + 3) & = & 0 \\ 2 Q - 5 & = & 0, & Q = 2.5100 gal / min \\ Q + 3 & = & 0, & Q = - 3100 gal / min not realistically possible \end{array}$

These roots check, but the negative root is not realistically possible, which means the only solution is $Q = 2.5$ $Q = 2.5$ 100 gal/min, (or 250 gal/min).

CAUTION

It is essential for the quadratic expression on the left to be equal to zero (on the right). The first step must be to write the equation in the form $a x^{2} + b x + c = 0.$ $a x^{2} + b x + c = 0.$

A number of equations involving fractions lead to quadratic equations after the fractions are eliminated. The following two examples illustrate the process of solving such equations with fractions. As discussed in Section 6.7, the fractions can be eliminated by multiplying each term of the equation by the LCD of all the denominators.

EXAMPLE 8 Fractional equation solved as quadratic

Solve for x: $\frac{1}{x} + 3 = \frac{2}{x + 2} .$ $\frac{1}{x} + 3 = \frac{2}{x + 2} .$

\begin{array}{rcll} \frac{x (x + 2)}{x} + 3 x (x + 2) & = & \frac{2 x (x + 2)}{x + 2} & \begin{array}{l} multiply each term by the \\ LCD, x (x + 2) \end{array} \\ x + 2 + 3 x^{2} + 6 x & = & 2 x & reduce each term \\ 3 x^{2} + 5 x + 2 & = & 0 & collect terms on left \\ (3 x + 2) (x + 1) & = & 0 & factor \\ 3 x + 2 & = & 0, x = - \frac{2}{3} & \begin{array}{l} set each factor equal \\ to zero and solve \end{array} \\ x + 1 & = & 0, x = - 1 \end{array}

$\begin{array}{rcll} \frac{x (x + 2)}{x} + 3 x (x + 2) & = & \frac{2 x (x + 2)}{x + 2} & \begin{array}{l} multiply each term by the \\ LCD, x (x + 2) \end{array} \\ x + 2 + 3 x^{2} + 6 x & = & 2 x & reduce each term \\ 3 x^{2} + 5 x + 2 & = & 0 & collect terms on left \\ (3 x + 2) (x + 1) & = & 0 & factor \\ 3 x + 2 & = & 0, x = - \frac{2}{3} & \begin{array}{l} set each factor equal \\ to zero and solve \end{array} \\ x + 1 & = & 0, x = - 1 \end{array}$

CAUTION

Remember, if either value gives division by zero, the root is extraneous, and must be excluded from the solution.

Both of these solutions check when substituted into the original equation.

EXAMPLE 9 Fractional equation—speed of truck

A lumber truck travels 60 mi from a sawmill to a lumber camp and then back in 7 h travel time. If the truck averages 5 mi/h less on the return trip than on the trip to the camp, find its average speed to the camp. See Fig. 7.1.

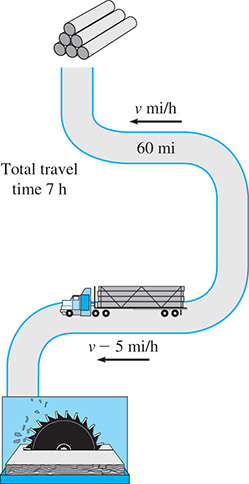
A lumber truck travels at v miles per hour to a lumber camp, and then returns at v minus 5 miles per hour. The trip is 60 miles each way and takes 7 hours total. — Fig. 7.1

Let $v = the$ $v = the$ average speed (in mi/h) of the truck going to the camp. This means that the average speed of the return trip was $(v - 5) mi / h .$ $(v - 5) mi / h .$

We also know that $d = v t$ $d = v t$ (distance equals speed times time), which tells us that $t = d / v .$ $t = d / v .$ Thus, the time for each part of the trip is the distance divided by the speed.

\begin{array}{rcl} \begin{array}{l} \begin{array}{c} time to \\ camp \end{array} & \begin{array}{c} camp \\ camp \end{array} \end{array} & \begin{array}{c} total \\ time \end{array} \\ \frac{60}{v} + \frac{60}{v - 5} & = & 7 \\ 60 (v - 5) + 60 v & = & 7 v (v - 5) & multiply each term by v (v - 5) \\ 7 v^{2} - 155 v + 300 & = & 0 & collect terms on the left \\ (7 v - 15) (v - 20) & = & 0 & factor \\ 7 v - 15 & = & 0, v = \frac{15}{7} & set each factor equal to zero and solve \\ v - 20 & = & 0, v = 20 \end{array}

$\begin{array}{rcl} \begin{array}{l} \begin{array}{c} time to \\ camp \end{array} & \begin{array}{c} camp \\ camp \end{array} \end{array} & \begin{array}{c} total \\ time \end{array} \\ \frac{60}{v} + \frac{60}{v - 5} & = & 7 \\ 60 (v - 5) + 60 v & = & 7 v (v - 5) & multiply each term by v (v - 5) \\ 7 v^{2} - 155 v + 300 & = & 0 & collect terms on the left \\ (7 v - 15) (v - 20) & = & 0 & factor \\ 7 v - 15 & = & 0, v = \frac{15}{7} & set each factor equal to zero and solve \\ v - 20 & = & 0, v = 20 \end{array}$

The value $v = 15/7 mi / h$ $v = 15/7 mi / h$ cannot be a solution because the return speed of 5 mi/h less would be negative. Thus, the solution is $v = 20 mi / h,$ $v = 20 mi / h,$ which means the return speed was 15 mi/h. The trip to the camp took 3 h, and the return took 4 h, which shows the solution checks.

The procedure used to solve quadratic equations in this section only works if we are able to factor the quadratic expression. In these cases, the solutions are rational numbers. Since not all quadratic expressions are factorable, other methods for solving quadratic equations will be discussed in the remaining sections of this chapter.

EXERCISES 7.1

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting quadratic equations.

In Example 3(a), change the $-$ $-$ sign before 7x to $+$ $+$ and then solve.
In Example 8, change the numerator of the first term to 2 and the numerator of the term on the right to 1 and then solve.

In Exercises 3–10, determine whether or not the given equations are quadratic. If the resulting form is quadratic, identify a, b, and c, with $a > 0.$ $a > 0.$ Otherwise, explain why the resulting form is not quadratic.

$x (x - 2) = 4$ $x (x - 2) = 4$
${(3 x - 2)}^{2} = 2$ ${(3 x - 2)}^{2} = 2$
$x^{2} = {(x + 2)}^{2}$ $x^{2} = {(x + 2)}^{2}$
$x (2 x^{2} + 5) = 7 + 2 x^{2}$ $x (2 x^{2} + 5) = 7 + 2 x^{2}$
$n (n^{2} + n - 1) = n^{3}$ $n (n^{2} + n - 1) = n^{3}$
${(T - 7)}^{2} = {(2 T + 3)}^{2}$ ${(T - 7)}^{2} = {(2 T + 3)}^{2}$
$y^{2} (y - 2) = 3 (y - 2)$ $y^{2} (y - 2) = 3 (y - 2)$
$z (z + 4) = (z + 1) (z + 5)$ $z (z + 4) = (z + 1) (z + 5)$

In Exercises 11–48, solve the given quadratic equations by factoring.

$x^{2} - 25 = 0$ $x^{2} - 25 = 0$
$B^{2} - 400 = 0$ $B^{2} - 400 = 0$
$4 y^{2} = 9$ $4 y^{2} = 9$
$2 x^{2} = 0.32$ $2 x^{2} = 0.32$
$x^{2} - 5 x - 14 = 0$ $x^{2} - 5 x - 14 = 0$
$x^{2} + x - 6 = 0$ $x^{2} + x - 6 = 0$
$R^{2} + 12 = 7 R$ $R^{2} + 12 = 7 R$
$x^{2} + 30 = 11 x$ $x^{2} + 30 = 11 x$
$40 x - 16 x^{2} = 0$ $40 x - 16 x^{2} = 0$
$15 L = 20 L^{2}$ $15 L = 20 L^{2}$
$12 m^{2} = 3$ $12 m^{2} = 3$
$9 = a^{2} x^{2}$ $9 = a^{2} x^{2}$
$3 x^{2} - 13 x + 4 = 0$ $3 x^{2} - 13 x + 4 = 0$
$A^{2} + 8 A + 16 = 0$ $A^{2} + 8 A + 16 = 0$
$4 x = 3 - 7 x^{2}$ $4 x = 3 - 7 x^{2}$
$4 x^{2} + 25 = 20 x$ $4 x^{2} + 25 = 20 x$
$6 x^{2} = 13 x - 6$ $6 x^{2} = 13 x - 6$
$6 z^{2} = 6 + 5 z$ $6 z^{2} = 6 + 5 z$
$4 x (x + 1) = 3$ $4 x (x + 1) = 3$
$t (43 + t) = 9 - 9 t^{2}$ $t (43 + t) = 9 - 9 t^{2}$
$6 y^{2} + b y = 2 b^{2}$ $6 y^{2} + b y = 2 b^{2}$
$2 x^{2} - 7 a x + 4 a^{2} = a^{2}$ $2 x^{2} - 7 a x + 4 a^{2} = a^{2}$
$8 s^{2} + 16 s = 90$ $8 s^{2} + 16 s = 90$
$18 t^{2} = 48 t - 32$ $18 t^{2} = 48 t - 32$
${(x + 2)}^{3} = x^{3} + 8$ ${(x + 2)}^{3} = x^{3} + 8$
$V (V^{2} - 4) = V^{2} (V - 1)$ $V (V^{2} - 4) = V^{2} (V - 1)$
${(x + a)}^{2} - b^{2} = 0$ ${(x + a)}^{2} - b^{2} = 0$
$b x^{2} - b = x - b^{2} x$ $b x^{2} - b = x - b^{2} x$
$x^{2} + 2 a x = b^{2} - a^{2}$ $x^{2} + 2 a x = b^{2} - a^{2}$
$x^{2} {(a^{2} + 2 a b + b^{2})}^{} = x (a + b)$ $x^{2} {(a^{2} + 2 a b + b^{2})}^{} = x (a + b)$
In Eq. (7.1), for $a = 2, b = - 7,$ $a = 2, b = - 7,$ and $c = 3,$ $c = 3,$ show that the sum of the roots is $- b / a .$ $- b / a .$
For the equation of Exercise 41 show that the product of the roots is c/a.
In finding the dimensions of a crate, the equation $12 x^{2} - 64 x + 64 = 0$ $12 x^{2} - 64 x + 64 = 0$ is used. Solve for x, if $x > 2.$ $x > 2.$
If a rocket is launched with an initial velocity of 320 ft/s, its height above ground after t seconds is given by $- 16 t^{2} + 320 t$ $- 16 t^{2} + 320 t$ (in ft). Find the times when the height is 0.
The voltage V across a semiconductor in a computer is given by $V = α I + β I^{2},$ $V = α I + β I^{2},$ where I is the current (in A). If a 6-V battery is conducted across the semiconductor, find the current if $α = 2 Ω$ $α = 2 Ω$ and $β = 0.5 Ω / A .$ $β = 0.5 Ω / A .$
The mass m (in Mg) of the fuel supply in the first-stage booster of a rocket is $m = 135 - 6 t - t^{2},$ $m = 135 - 6 t - t^{2},$ where t is the time (in s) after launch. When does the booster run out of fuel?
The power P (in MW) produced between midnight and noon by a nuclear power plant is $P = 4 h^{2} - 48 h + 744,$ $P = 4 h^{2} - 48 h + 744,$ where h is the hour of the day. At what time is the power 664 MW?
In determining the speed s (in mi/h) of a car while studying its fuel economy, the equation $s^{2} - 16 s = 3072$ $s^{2} - 16 s = 3072$ is used. Find s.

In Exercises 49 and 50, find the indicated quadratic equations.

Find a quadratic equation for which the solutions are 0.5 and 2.
Find a quadratic equation for which the solutions are a and b.

In Exercises 50 and 51, although the equations are not quadratic, factoring will lead to one quadratic factor and the solution can be completed by factoring as with a quadratic equation. Find the three roots of each equation.

$x^{3} - x = 0$ $x^{3} - x = 0$
$x^{3} - 4 x^{2} - x + 4 = 0$ $x^{3} - 4 x^{2} - x + 4 = 0$

In Exercises 53–56, solve the given equations involving fractions.

$\frac{1}{x - 3} + \frac{4}{x} = 2$ $\frac{1}{x - 3} + \frac{4}{x} = 2$
$2 - \frac{1}{x} = \frac{3}{x + 2}$ $2 - \frac{1}{x} = \frac{3}{x + 2}$
$\frac{1}{2 x} - \frac{3}{4} = \frac{1}{2 x + 3}$ $\frac{1}{2 x} - \frac{3}{4} = \frac{1}{2 x + 3}$
$\frac{x}{2} + \frac{1}{x - 3} = 3$ $\frac{x}{2} + \frac{1}{x - 3} = 3$

In Exercises 57–60, set up the appropriate quadratic equations and solve.

The spring constant k is the force F divided by the amount x the spring stretches $(k = F / x) .$ $(k = F / x) .$ See Fig. 7.2(a). For two springs in series [see Fig. 7.2(b)], the reciprocal of the spring constant $k_{c}$ $k_{c}$ for the combination equals the sum of the reciprocals of the individual spring constants. Find the spring constants for each of two springs in series if $k_{c} = 2 N / cm$ $k_{c} = 2 N / cm$ and one spring constant is 3 N/cm more than the other.

Fig. 7.2
The combined resistance R of two resistances $R_{1}$ $R_{1}$ and $R_{2}$ $R_{2}$ connected in parallel [see Fig. 7.3(a)] is equal to the product of the individual resistances divided by their sum. If the two resistances are connected in series [see Fig. 7.3(b)], their combined resistance is the sum of their individual resistances. If two resistances connected in parallel have a combined resistance of $3.0 Ω$ $3.0 Ω$ and the same two resistances have a combined resistance of $16 Ω$ $16 Ω$ when connected in series, what are the resistances?

Fig. 7.3

Figure 7.3 Full Alternative Text
A hydrofoil made the round-trip of 120 km between two islands in 3.5 h of travel time. If the average speed going was 10 km/h less than the average speed returning, find these speeds.
A rectangular solar panel is 20 cm by 30 cm. By adding the same amount to each dimension, the area is doubled. How much is added?

Answers to Practice Exercises

$x = - 7, x = 3$ $x = - 7, x = 3$
$x = 1/3, x = 1/3$ $x = 1/3, x = 1/3$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

	To show this equation in the form of Eq. (7.1), it can be written as $1 x^{2} + (- 4) x + (- 5) = 0.$ $1 x^{2} + (- 4) x + (- 5) = 0.$
	Because there is no `x`-term, $b = 0.$ $b = 0.$
	Because no constant appears, $c = 0.$ $c = 0.$
$(m - 3) x^{2} - m x + 7 = 0$ $(m - 3) x^{2} - m x + 7 = 0$	The constants in Eq. (7.1) may include literal expressions. In this case, $m - 3$ $m - 3$ takes the place of a –m takes the place of `b`, and $c = 7.$ $c = 7.$
$4 x^{2} - 2 x = x^{2}$ $4 x^{2} - 2 x = x^{2}$	After all nonzero terms have been collected on the left side, the equation becomes $3 x^{2} - 2 x = 0.$ $3 x^{2} - 2 x = 0.$
${(x + 1)}^{2} = 4$ ${(x + 1)}^{2} = 4$	Expanding the left side and collecting all nonzero terms on the left, we have $x^{2} + 2 x - 3 = 0.$ $x^{2} + 2 x - 3 = 0.$

Table of Contents for 7.1 Quadratic Equations; Solution by Factoring

Create new playlist

Sign In

Sign Up

Table of Contents for
7.1 Quadratic Equations; Solution by Factoring