Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

4.3 Values of the Trigonometric Functions

Function Values Using Geometry • Function Values from Calculator • Inverse Trigonometric Functions • Accuracy of Trigonometric Functions • Reciprocal Functions

We often need values of the trigonometric functions for angles measured in degrees. One way to find some of these values for particular angles is to use certain basic facts from geometry. This is illustrated in the next two examples.

EXAMPLE 1 Function values of 30 ° and 60 °

From geometry, we find that in a right triangle, the side opposite a $30 °$ $30 °$ angle is one-half of the hypotenuse. Therefore, in Fig. 4.18, letting $y = 1$ $y = 1$ and $r = 2,$ $r = 2,$ and using the Pythagorean theorem, $x = \sqrt{2^{2} - 1^{2}} = \sqrt{3} .$ $x = \sqrt{2^{2} - 1^{2}} = \sqrt{3} .$ Now with $x = \sqrt{3}, y = 1,$ $x = \sqrt{3}, y = 1,$ and $r = 2,$ $r = 2,$

\sin 30 ° = \frac{1}{2} \cos 30 ° = \frac{\sqrt{3}}{2} \tan 30 ° = \frac{1}{\sqrt{3}}

$\sin 30 ° = \frac{1}{2} \cos 30 ° = \frac{\sqrt{3}}{2} \tan 30 ° = \frac{1}{\sqrt{3}}$

The counterclockwise angle 30 degrees with a terminal side that passes through (square root of 3, 1) with length r = 2 and vertical height y = 1. — Fig. 4.18

Using this same method, we find the functions of $60 °$ $60 °$ to be (see Fig. 4.19)

\sin 60 ° = \frac{\sqrt{3}}{2} \cos 60 ° = \frac{1}{2} \tan 60 ° = \sqrt{3}

$\sin 60 ° = \frac{\sqrt{3}}{2} \cos 60 ° = \frac{1}{2} \tan 60 ° = \sqrt{3}$

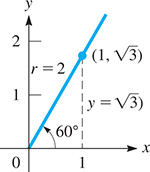
The counterclockwise angle 30 degrees with a terminal side that passes through (1, square root of 3) with length r = 2 and vertical height y = square root of 3. — Fig. 4.19

EXAMPLE 2 Function values of 45 °

Find $\sin 45 °$ $\sin 45 °$ , $\cos 45 °$ $\cos 45 °$ , and $\tan 45 °$ $\tan 45 °$ .

If we place an isosceles right triangle with one of its $45 °$ $45 °$ angles in standard position and hypotenuse along the radius vector (see Fig. 4.20), the terminal side passes through (1, 1), since the legs of the triangle are equal. Using this point, $x = 1, y = 1,$ $x = 1, y = 1,$ and $r = \sqrt{2} .$ $r = \sqrt{2} .$ Thus,

\sin 45 ° = \frac{1}{\sqrt{2}} \cos 45 ° = \frac{1}{\sqrt{2}} \tan 45 ° = 1

$\sin 45 ° = \frac{1}{\sqrt{2}} \cos 45 ° = \frac{1}{\sqrt{2}} \tan 45 ° = 1$

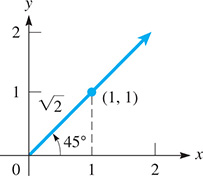
The counterclockwise angle 45 degrees with a terminal side that passes through (1, 1) with length square root of 2. — Fig. 4.20

In Examples 1 and 2, we have given exact values. Decimal approximations are also given in the following table that summarizes the results for $30 °$ $30 °$ , $45 °$ $45 °$ , and $60 °$ $60 °$ .

Trigonometric Functions of

30 °, 45 °,

$30 °, 45 °,$ and

60 °

$60 °$

	(exact values)			(decimal approximations)
$θ$ $θ$	$30 °$ $30 °$	$45 °$ $45 °$	$60 °$ $60 °$	$30 °$ $30 °$	$45 °$ $45 °$	$60 °$ $60 °$
$\sin θ$ $\sin θ$	$\frac{1}{2}$ $\frac{1}{2}$	$\frac{1}{\sqrt{2}}$ $\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	0.500	0.707	0.866
$\cos θ$ $\cos θ$	$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$ $\frac{1}{\sqrt{2}}$	$\frac{1}{2}$ $\frac{1}{2}$	0.866	0.707	0.500
$\tan θ$ $\tan θ$	$\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$	1	$\sqrt{3}$ $\sqrt{3}$	0.577	1.000	1.732

Another way to find values of the functions is to use a scale drawing. Measure the angle with a protractor, then measure directly the values of x, y, and r for some point on the terminal side, and finally use the proper ratios to evaluate the functions. However, this method is only approximate, and geometric methods work only for a limited number of angles. As it turns out, it is possible to find these values to any required accuracy through more advanced methods (using calculus and what are known as power series).

Values of $\sin θ, \cos θ,$ $\sin θ, \cos θ,$ and $\tan θ$ $\tan θ$ are programmed into graphing calculators. For the remainder of this chapter, be sure that your calculator is set for degrees (not radians). The following examples illustrate using a calculator to find trigonometric values.

EXAMPLE 3 Values from calculator

Using a calculator to find the value of $\tan 67.36 °$ $\tan 67.36 °$ , first enter the function and then the angle, just as it is written. The resulting display is shown in Fig. 4.21.

A calculator screen with input tangent of, 67.36, and output 2.397626383. — Fig. 4.21

Therefore, $\tan 67.36 ° = 2.397626383.$ $\tan 67.36 ° = 2.397626383.$

Not only are we able to find values of the trigonometric functions if we know the angle, but we can also find the angle if we know that value of a function. In doing this, we are actually using another important type of mathematical function, an inverse trigonometric function. They are discussed in detail in Chapter 20. For the purpose of using a calculator at this point, it is sufficient to recognize and understand the notation that is used.

The notation for “the angle whose sine is x” is $\sin^{- 1} x .$ $\sin^{- 1} x .$ This is called the inverse sine function. Equivalent meanings are given to $\cos^{- 1} x$ $\cos^{- 1} x$ (the angle whose cosine is x) and $\tan^{- 1} x$ $\tan^{- 1} x$ (the angle whose tangent is x).

CAUTION

Carefully note that the $- 1$ $- 1$ used with a trigonometric function in this way shows an inverse trigonometric function and is not a negative exponent ( $\sin^{- 1} x$ $\sin^{- 1} x$ represents an angle, not a function of an angle).

On a calculator, the $\sin^{- 1}$ $\sin^{- 1}$ key (usually obtained by pressing ) is used to find the angle when the sine of that angle is known. The following example illustrates the use of the similar $\cos^{- 1}$ $\cos^{- 1}$ key.

EXAMPLE 4 Inverse function value from calculator

If $\cos θ = 0.3527,$ $\cos θ = 0.3527,$ which means that $θ = \cos^{- 1} 0.3527$ $θ = \cos^{- 1} 0.3527$ ( $θ$ $θ$ is the angle whose cosine is 0.3527), we can use a calculator to find $θ .$ $θ .$ The display is shown in Fig. 4.22.

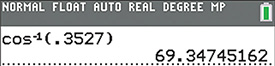
A calculator screen with input inverse of cosine of, 0.3527, and output 69.34745162. — Fig. 4.22

Therefore, $θ = 69.35 °$ $θ = 69.35 °$ (rounded off).

When using the trigonometric functions, the angle is often approximate. Angles of $2.3 °$ $2.3 °$ , $92.3 °$ $92.3 °$ , and $182.3 °$ $182.3 °$ are angles with equal accuracy, which shows that the accuracy of an angle does not depend on the number of digits shown. The measurement of an angle and the accuracy of its trigonometric functions are shown in Table 4.1:

Table 4.1 Angles and Accuracy of Trigonometric Functions

Measurements of Angle to Nearest	Accuracy of Trigonometric Function
$1 °$ $1 °$	2 significant digits
$0.1 °$ $0.1 °$ or $10'$ $10'$	3 significant digits
$0.01 °$ $0.01 °$ or $1'$ $1'$	4 significant digits

We rounded off the result in Example 4 according to this table.

Although we can usually set up the solution of a problem in terms of the sine, cosine, or tangent, there are times when a value of the cotangent, secant, or cosecant is used. We now show how values of these functions are found on a calculator.

NOTE

[Because the reciprocal of x equals $x^{- 1},$ $x^{- 1},$ we can use the $x^{- 1}$ $x^{- 1}$ key along with the sin, cos, and tan keys, to find the values of $\csc θ, \sec θ,$ $\csc θ, \sec θ,$ and $\cot θ .$ $\cot θ .$ ]

From the definitions, $\csc θ = r / y$ $\csc θ = r / y$ and $\sin θ = y / r .$ $\sin θ = y / r .$ This means the value of $\csc θ$ $\csc θ$ is the reciprocal of the value of $\sin θ .$ $\sin θ .$ Again, using the definitions, we find that the value of $\sec θ$ $\sec θ$ is the reciprocal of $\cos θ$ $\cos θ$ and the value of $\cot θ$ $\cot θ$ is the reciprocal of $\tan θ .$ $\tan θ .$

EXAMPLE 5 Reciprocal functions value from calculator

To find the value of $\sec 27.82 °$ $\sec 27.82 °$ , we use the fact that

\sec 27.82 ° = \frac{1}{\cos 27.82 °} = 1.131 or \sec 27.82 ° = {(\cos 27.82 °)}^{- 1} = 1.131

$\sec 27.82 ° = \frac{1}{\cos 27.82 °} = 1.131 or \sec 27.82 ° = {(\cos 27.82 °)}^{- 1} = 1.131$

Either of the above two options can be evaluated on a calculator to obtain the result 1.131, which has been rounded according to Table 4.1.

EXAMPLE 6 Given a function—find `θ`

To find the value of $θ$ $θ$ if $\cot θ = 0.354,$ $\cot θ = 0.354,$ we use the fact that

\tan θ = \frac{1}{\cot θ} = \frac{1}{0.354}

$\tan θ = \frac{1}{\cot θ} = \frac{1}{0.354}$

Therefore, $θ = \tan^{- 1} (\frac{1}{0.354}) = 70.5 °$ $θ = \tan^{- 1} (\frac{1}{0.354}) = 70.5 °$ (rounded off).

EXAMPLE 7 Given one function—find another

Find $\sin θ$ $\sin θ$ if $\sec θ = 2.504.$ $\sec θ = 2.504.$

Since the value of $\sec θ$ $\sec θ$ is given, we know that $\cos θ = 1/2.504.$ $\cos θ = 1/2.504.$ This in turn tells us that $θ = \cos^{- 1} (\frac{1}{2.504}) \approx 66.46176 °$ $θ = \cos^{- 1} (\frac{1}{2.504}) \approx 66.46176 °$ (extra significant digits are retained since this is an intermediate step).

Therefore, $\sin θ = \sin (66.46176 °) = 0.9168$ $\sin θ = \sin (66.46176 °) = 0.9168$ (see Fig. 4.23).

A calculator screen with input inverse cosine of, 1 divided by 2.504, and output 66.46176102; input sine of, 66.46176102, and output 0.9167937466. — Fig. 4.23

The following example illustrates the use of the value of a trigonometric function in an applied problem. We consider various types of applications later in the chapter.

EXAMPLE 8 Evaluating cosine—rocket velocity

When a rocket is launched, its horizontal velocity $v_{x}$ $v_{x}$ is related to the velocity v with which it is fired by the equation $v_{x} = v \cos θ .$ $v_{x} = v \cos θ .$ Here, $θ$ $θ$ is the angle between the horizontal and the direction in which it is fired (see Fig. 4.24). Find $v_{x}$ $v_{x}$ if $v = 1250 m / s$ $v = 1250 m / s$ and $θ = 36.0 ° .$ $θ = 36.0 ° .$

A diagram of a rocket launching, modeled by an angle of 36.0 degrees in standard position. The initial side is v sub x, and the terminal side is v. The rocket is launched along the terminal side. — Fig. 4.24

Substituting the given values of v and $θ$ $θ$ in $v_{x} = v \cos θ,$ $v_{x} = v \cos θ,$ we have

\begin{array}{rcl} v_{x} & = & 1250 \cos 36.0 ° \\ = & 1010 m / s \end{array}

$\begin{array}{rcl} v_{x} & = & 1250 \cos 36.0 ° \\ = & 1010 m / s \end{array}$

Therefore, the horizontal velocity is 1010 m/s (rounded off).

EXERCISES 4.3

In Exercises 1–4, make the given changes in the indicated examples of this section and then find the indicated values.

In Example 4, change $\cos θ$ $\cos θ$ to $\sin θ$ $\sin θ$ and then find the angle.
In Example 5, change $\sec 27.82 °$ $\sec 27.82 °$ to $\csc 27.82 °$ $\csc 27.82 °$ and then find the value.
In Example 6, change 0.354 to 0.345 and then find the angle.
In Example 7, change $\sin θ$ $\sin θ$ to $\tan θ$ $\tan θ$ and then find the value.

In Exercises 5–20, find the values of the trigonometric functions. Round off results according to Table 4.1.

$\sin 34.9 °$ $\sin 34.9 °$
$\cos 72.5 °$ $\cos 72.5 °$
$\tan 57.6 °$ $\tan 57.6 °$
$\sin 36.0 °$ $\sin 36.0 °$
$\cos 15.71 °$ $\cos 15.71 °$
$\tan 8.653 °$ $\tan 8.653 °$
$\sin 88 °$ $\sin 88 °$
$\cos 0.7 °$ $\cos 0.7 °$
$\cot 57.86 °$ $\cot 57.86 °$
$\csc 22.81 °$ $\csc 22.81 °$
$\sec 80.4 °$ $\sec 80.4 °$
$\cot 41.8 °$ $\cot 41.8 °$
$\csc 0.49 °$ $\csc 0.49 °$
$\sec 7.8 °$ $\sec 7.8 °$
$\cot 85.96 °$ $\cot 85.96 °$
$\csc 76.30 °$ $\csc 76.30 °$

In Exercises 21–36, find $θ$ $θ$ for each of the given trigonometric functions. Round off results according to Table 4.1.

$\cos θ = 0.3261$ $\cos θ = 0.3261$
$\tan θ = 2.470$ $\tan θ = 2.470$
$\sin θ = 0.9114$ $\sin θ = 0.9114$
$\cos θ = 0.0427$ $\cos θ = 0.0427$
$\tan θ = 0.317$ $\tan θ = 0.317$
$\sin θ = 1.09$ $\sin θ = 1.09$
$\cos θ = 0.65007$ $\cos θ = 0.65007$
$\tan θ = 5.7706$ $\tan θ = 5.7706$
$\csc θ = 2.574$ $\csc θ = 2.574$
$\sec θ = 2.045$ $\sec θ = 2.045$
$\cot θ = 0.0606$ $\cot θ = 0.0606$
$\csc θ = 1.002$ $\csc θ = 1.002$
$\sec θ = 0.305$ $\sec θ = 0.305$
$\cot θ = 14.4$ $\cot θ = 14.4$
$\csc θ = 8.26$ $\csc θ = 8.26$
$\cot θ = 0.1519$ $\cot θ = 0.1519$

In Exercises 37–40, use a protractor to draw the given angle. Measure off 10 units (centimeters are convenient) along the radius vector. Then measure the corresponding values of x and y. From these values, determine the trigonometric functions of the angle.

$40 °$ $40 °$
$75 °$ $75 °$
$15 °$ $15 °$
$53 °$ $53 °$

In Exercises 41–44, use a calculator to verify the given relationships or statements. $[\sin^{2} θ = {(\sin θ)}^{2}]$ $[\sin^{2} θ = {(\sin θ)}^{2}]$

$\frac{\sin 43.7 °}{\cos 43.7 °} = \tan 43.7 °$ $\frac{\sin 43.7 °}{\cos 43.7 °} = \tan 43.7 °$
$\sin^{2} 77.5 ° + \cos^{2} 77.5 ° = 1$ $\sin^{2} 77.5 ° + \cos^{2} 77.5 ° = 1$
$\tan 70 ° = \frac{\tan 30 ° + \tan 40 °}{1 - (\tan 30 °) (\tan 40 °)}$ $\tan 70 ° = \frac{\tan 30 ° + \tan 40 °}{1 - (\tan 30 °) (\tan 40 °)}$
$\sin 78.4 ° = 2 (\sin 39.2 °) (\cos 39.2 °)$ $\sin 78.4 ° = 2 (\sin 39.2 °) (\cos 39.2 °)$

In Exercises 45–50, explain why the given statements are true for an acute angle $θ$ $θ$ .

$\sin θ$ $\sin θ$ is always between 0 and 1.
$\tan θ$ $\tan θ$ can equal any positive real number.
$\cos θ$ $\cos θ$ decreases in value as $θ$ $θ$ increases from $0 °$ $0 °$ to $90 °$ $90 °$ .
The value of $\sec θ$ $\sec θ$ is never less than 1.
$\sin θ + \cos θ > 1,$ $\sin θ + \cos θ > 1,$ if $θ$ $θ$ is acute.
If $θ < 45 °, \sin θ < \cos θ .$ $θ < 45 °, \sin θ < \cos θ .$

In Exercises 51–54, find the values of the indicated trigonometric functions if $θ$ $θ$ is an acute angle.

Find $\sin θ,$ $\sin θ,$ given $\tan θ = 1.936.$ $\tan θ = 1.936.$
Find $\cos θ,$ $\cos θ,$ given $\sin θ = 0.6725.$ $\sin θ = 0.6725.$
Find $\tan θ,$ $\tan θ,$ given $\sec θ = 1.3698.$ $\sec θ = 1.3698.$
Find $\csc θ,$ $\csc θ,$ given $\cos θ = 0.1063.$ $\cos θ = 0.1063.$

In Exercises 55–60, solve the given problems.

According to Snell’s law, if a ray of light passes from air into water with an angle of incidence of $45.0 °$ $45.0 °$ , then the angle of refraction $θ_{r}$ $θ_{r}$ is given by the equation $\sin 45.0 ° = 1.33 \sin θ_{r} .$ $\sin 45.0 ° = 1.33 \sin θ_{r} .$ Find $θ_{r} .$ $θ_{r} .$
If the backup camera on a car is mounted at a height h above the road and is angled downward (from the horizontal) at an angle $θ,$ $θ,$ then the distance x along the road between the car and the point at which the camera is directed is given by $x = \frac{h}{\tan θ} .$ $x = \frac{h}{\tan θ} .$ Find x if $h = 24.0 in .$ $h = 24.0 in .$ and $θ = 15.0 ° .$ $θ = 15.0 ° .$
A brace is used in the structure shown in Fig. 4.25. Its length is $l = a (\sec θ + \csc θ) .$ $l = a (\sec θ + \csc θ) .$ Find l if $a = 28.0 cm$ $a = 28.0 cm$ and $θ = 34.5 ° .$ $θ = 34.5 ° .$

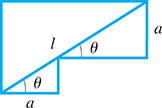
Fig. 4.25

Figure 4.25 Full Alternative Text
The sound produced by a jet engine was measured at a distance of 100 m in all directions. The loudness d of the sound (in decibels) was found to be $d = 70.0 + 30.0 \cos θ,$ $d = 70.0 + 30.0 \cos θ,$ where the $0 °$ $0 °$ line was directed in front of the engine. Calculate d for $θ = 54.5 ° .$ $θ = 54.5 ° .$
The signal from an AM radio station with two antennas d meters apart has a wavelength $λ$ $λ$ (in m). The intensity of the signal depends on the angle $θ$ $θ$ as shown in Fig. 4.26. An angle of minimum intensity is given by $\sin θ = 1.50 λ / d .$ $\sin θ = 1.50 λ / d .$ Find $θ$ $θ$ if $λ = 200 m$ $λ = 200 m$ and $d = 400 m .$ $d = 400 m .$

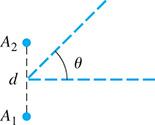
Fig. 4.26
A submarine dives such that the horizontal distance h it moves and the vertical distance v it dives are related by $v = h \tan θ .$ $v = h \tan θ .$ Here, $θ$ $θ$ is the angle of the dive, as shown in Fig. 4.27. Find $θ$ $θ$ if $h = 2.35 mi$ $h = 2.35 mi$ and $v = 1.52 mi .$ $v = 1.52 mi .$

Fig. 4.27

Answers to Practice Exercises

0.216
$46.10 °$ $46.10 °$
0.664
$31.68 °$ $31.68 °$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 4.3 Values of the Trigonometric Functions

Create new playlist

Sign In

Sign Up

Table of Contents for
4.3 Values of the Trigonometric Functions