Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

7.3 The Quadratic Formula

The Quadratic Formula • Character of the Roots of a Quadratic Equation

We now use the method of completing the square to derive a general formula that may be used for the solution of any quadratic equation.

Consider the general quadratic equation:

a x^{2} + b x + c = 0 (a \neq 0)

$a x^{2} + b x + c = 0 (a \neq 0)$

When we divide through by a, we obtain

x^{2} + \frac{b}{a} x + \frac{c}{a} = 0

$x^{2} + \frac{b}{a} x + \frac{c}{a} = 0$

Subtracting c/a from each side, we have

x^{2} + \frac{b}{a} x = - \frac{c}{a}

$x^{2} + \frac{b}{a} x = - \frac{c}{a}$

Half of b/a is b/2a, which squared is $b^{2} / 4 a^{2} .$ $b^{2} / 4 a^{2} .$ Adding $b^{2} / 4 a^{2}$ $b^{2} / 4 a^{2}$ to each side gives us

x^{2} + \frac{b}{a} x + \frac{b^{2}}{4 a^{2}} = - \frac{c}{a} + \frac{b^{2}}{4 a^{2}}

$x^{2} + \frac{b}{a} x + \frac{b^{2}}{4 a^{2}} = - \frac{c}{a} + \frac{b^{2}}{4 a^{2}}$

Writing the left side as a perfect square and combining fractions on the right side,

{(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}

${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$

Equating $x + \frac{b}{2 a}$ $x + \frac{b}{2 a}$ to the positive and negative square root of the right side,

x + \frac{b}{2 a} = \frac{\pm \sqrt{b^{2} - 4 a c}}{2 a}

$x + \frac{b}{2 a} = \frac{\pm \sqrt{b^{2} - 4 a c}}{2 a}$

When we subtract b/2a from each side and simplify the resulting expression, we obtain the quadratic formula:

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ (7.4)

The quadratic formula gives us a quick general way of solving any quadratic equation. We need only write the equation in the standard form $a x^{2} + b x + c = 0;$ $a x^{2} + b x + c = 0;$ substitute the values of a, b, and c into the formula; and simplify.

EXAMPLE 1 Quadratic formula—rational roots

Solve: 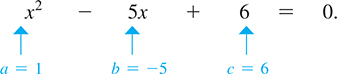x squared minus 5 x + 6 = 0. The x squared coefficient value of a is 1, 5 x coefficient value of b is negative 5 and 6 constant value of c is 6.

Here, using the indicated values of a, b, and c in the quadratic formula, we have

\begin{array}{l} x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (1) (6)}}{2 (1)} = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2} \\ x = \frac{5 + 1}{2} = 3 or x = \frac{5 - 1}{2} = 2 \end{array}

$\begin{array}{l} x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (1) (6)}}{2 (1)} = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2} \\ x = \frac{5 + 1}{2} = 3 or x = \frac{5 - 1}{2} = 2 \end{array}$

The roots $x = 3$ $x = 3$ and $x = 2$ $x = 2$ check when substituted in the original equation.

CAUTION

It must be emphasized that, in using the quadratic formula, the entire expression $- b \pm \sqrt{b^{2} - 4 a c}$ $- b \pm \sqrt{b^{2} - 4 a c}$ is divided by 2a. It is a relatively common error to divide only the radical $\sqrt{b^{2} - 4 a c} .$ $\sqrt{b^{2} - 4 a c} .$

EXAMPLE 2 Quadratic formula—irrational roots

Solve: 2 x squared minus 7 x minus 5 = 0. The 2 x squared coefficient value of a is 2, 7 x coefficient value of b is negative 7 and 5 constant value of c is negative 5.

Substituting the values for a, b, and c in the quadratic formula, we have

\begin{array}{l} x = \frac{- (- 7) \pm \sqrt{{(- 7)}^{2} - 4 (2) (- 5)}}{2 (2)} = \frac{7 \pm \sqrt{49 + 40}}{4} = \frac{7 \pm \sqrt{89}}{4} \\ x = \frac{7 + \sqrt{89}}{4} = 4.108 or x = \frac{7 - \sqrt{89}}{4} = - 0.6085 \end{array}

$\begin{array}{l} x = \frac{- (- 7) \pm \sqrt{{(- 7)}^{2} - 4 (2) (- 5)}}{2 (2)} = \frac{7 \pm \sqrt{49 + 40}}{4} = \frac{7 \pm \sqrt{89}}{4} \\ x = \frac{7 + \sqrt{89}}{4} = 4.108 or x = \frac{7 - \sqrt{89}}{4} = - 0.6085 \end{array}$

The exact roots are $x = \frac{7 \pm \sqrt{89}}{4}$ $x = \frac{7 \pm \sqrt{89}}{4}$ (this form is often used when the roots are irrational). Approximate decimal values are $x = 4.108$ $x = 4.108$ and $x = - 0.6085.$ $x = - 0.6085.$

EXAMPLE 3 Quadratic formula—double root

Solve: $9 x^{2} + 24 x + 16 = 0.$ $9 x^{2} + 24 x + 16 = 0.$

In this example, $a = 9, b = 24,$ $a = 9, b = 24,$ and $c = 16.$ $c = 16.$ Thus,

x = \frac{- 24 \pm \sqrt{24^{2} - 4 (9) (16)}}{2 (9)} = \frac{- 24 \pm \sqrt{576 - 576}}{18} = \frac{- 24 \pm 0}{18} = - \frac{4}{3}

$x = \frac{- 24 \pm \sqrt{24^{2} - 4 (9) (16)}}{2 (9)} = \frac{- 24 \pm \sqrt{576 - 576}}{18} = \frac{- 24 \pm 0}{18} = - \frac{4}{3}$

NOTE

[Here, both roots are $- \frac{4}{3},$ $- \frac{4}{3},$ so $x = - \frac{4}{3}$ $x = - \frac{4}{3}$ is called a double root. We will always get a double root when $b^{2} - 4 a c = 0,$ $b^{2} - 4 a c = 0,$ as in this case.]

EXAMPLE 4 Quadratic formula—imaginary roots

Solve: $3 x^{2} - 5 x + 4 = 0.$ $3 x^{2} - 5 x + 4 = 0.$

In this example, $a = 3, b = - 5,$ $a = 3, b = - 5,$ and $c = 4.$ $c = 4.$ Therefore,

x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (3) (4)}}{2 (3)} = \frac{5 \pm \sqrt{25 - 48}}{6} = \frac{5 \pm \sqrt{- 23}}{6}

$x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (3) (4)}}{2 (3)} = \frac{5 \pm \sqrt{25 - 48}}{6} = \frac{5 \pm \sqrt{- 23}}{6}$

NOTE

[These roots contain imaginary numbers. This happens if $b^{2} - 4 a c < 0.$ $b^{2} - 4 a c < 0.$ ]

The previous examples illustrate the character of the roots of a quadratic equation. If a, b, and c are rational numbers, by noting the value of $b^{2} - 4 a c$ $b^{2} - 4 a c$ (called the discriminant), we have the following:

We can use the value of $b^{2} - 4 a c$ $b^{2} - 4 a c$ to help in checking the roots or in finding the character of the roots without having to solve the equation completely.

EXAMPLE 5 Quadratic formula—literal numbers

The equation $s = s_{0} + v_{0} t - \frac{1}{2} {g t}^{2}$ $s = s_{0} + v_{0} t - \frac{1}{2} {g t}^{2}$ is used in the analysis of projectile motion (see Fig. 7.5). Solve for t.

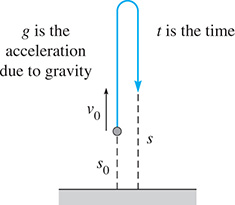
A ball begins at s sub naught and is thrown at v sub naught into the air. After time t, it is at s. G is the acceleration due to gravity. — Fig. 7.5

g t^{2} - 2 v_{0} t - 2 (s_{0} - s) = 0 multiply by - 2, put in form a x^{2} + b x + c = 0

$g t^{2} - 2 v_{0} t - 2 (s_{0} - s) = 0 multiply by - 2, put in form a x^{2} + b x + c = 0$

In this form, we see that $a = g, b = - 2 v_{0},$ $a = g, b = - 2 v_{0},$ and $c = - 2 (s_{0} - s) :$ $c = - 2 (s_{0} - s) :$

\begin{array}{rcl} t & = & \frac{- (- 2 v_{0}) \pm \sqrt{{(- 2 v_{0})}^{2} - 4 g (- 2) (s_{0} - s)}}{2 g} \\ = & \frac{2 v_{0} \pm \sqrt{4 (v_{0}^{2} + 2 g s_{0} - 2 g s)}}{2 g} \\ = & \frac{2 v_{0} \pm 2 \sqrt{v_{0}^{2} + 2 g s_{0} - 2 g s}}{2 g} \\ = & \frac{v_{0} \pm \sqrt{v_{0}^{2} + 2 g s_{0} - 2 g s}}{g} \end{array}

$\begin{array}{rcl} t & = & \frac{- (- 2 v_{0}) \pm \sqrt{{(- 2 v_{0})}^{2} - 4 g (- 2) (s_{0} - s)}}{2 g} \\ = & \frac{2 v_{0} \pm \sqrt{4 (v_{0}^{2} + 2 g s_{0} - 2 g s)}}{2 g} \\ = & \frac{2 v_{0} \pm 2 \sqrt{v_{0}^{2} + 2 g s_{0} - 2 g s}}{2 g} \\ = & \frac{v_{0} \pm \sqrt{v_{0}^{2} + 2 g s_{0} - 2 g s}}{g} \end{array}$

EXAMPLE 6 Quadratic formula—patio dimensions

A rectangular area 17.0 m long and 12.0 m wide is to be used for a patio with a rectangular pool. One end and one side of the patio area around the pool (the chairs, sunning, etc.) are to be the same width. The other end with the diving board is to be twice as wide, and the other side is to be three times as wide as the narrow side. The pool area is to be $96.5 m^{2} .$ $96.5 m^{2} .$ What are the widths of the patio ends and sides, and the dimensions of the pool? See Fig. 7.6.

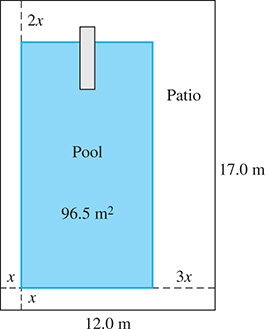
A rectangular pool with area 96.5 meters squared is surrounded by a patio with length 17.0 meters and width 12.0 meters. — Fig. 7.6

Figure 7.6 Full Alternative Text

First, let $x = the$ $x = the$ width of the narrow end and side of the patio. The other end is then 2x in width, and the other side is 3x in width. Because the pool area is $96.5 m^{2},$ $96.5 m^{2},$ we have

\begin{array}{c} \begin{array}{rcl} pool length pool width & pool area \\ (17.0 - 3 x) (12.0 - 4 x) & = & 96.5 \\ 204 - 68.0 x - 36.0 x + 12 x^{2} & = & 96.5 \\ 12 x^{2} - 104.0 x + 107.5 & = & 0 \end{array} \\ x = \frac{- (- 104.0) \pm \sqrt{{(- 104.0)}^{2} - 4 (12) (107.5)}}{2 (12)} = \frac{104.0 \pm \sqrt{5656}}{24} \end{array}

$\begin{array}{c} \begin{array}{rcl} pool length pool width & pool area \\ (17.0 - 3 x) (12.0 - 4 x) & = & 96.5 \\ 204 - 68.0 x - 36.0 x + 12 x^{2} & = & 96.5 \\ 12 x^{2} - 104.0 x + 107.5 & = & 0 \end{array} \\ x = \frac{- (- 104.0) \pm \sqrt{{(- 104.0)}^{2} - 4 (12) (107.5)}}{2 (12)} = \frac{104.0 \pm \sqrt{5656}}{24} \end{array}$

Evaluating, we get $x = 7.5 m$ $x = 7.5 m$ and $x = 1.2 m .$ $x = 1.2 m .$ The value 7.5 m cannot be the required result because the width of the patio would be greater than the width of the entire area. For $x = 1.2 m,$ $x = 1.2 m,$ the pool would have a length 13.4 m and width 7.2 m. These give an area of $96.5 m^{2},$ $96.5 m^{2},$ which checks. The widths of the patio area are then 1.2 m, 1.2 m, 2.4 m, and 3.6 m.

EXERCISES 7.3

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting equations by the quadratic formula.

In Example 1, change the $-$ $-$ sign before 5x to $+ .$ $+ .$
In Example 2, change the coefficient of $x^{2}$ $x^{2}$ from 2 to 3.

In Exercises 3–34, solve the given quadratic equations using the quadratic formula. If there are no real roots, state this as the answer. Exercises 3–6 are the same as Exercises 13–16 of Section 7.2.

$x^{2} + 2 x - 15 = 0$ $x^{2} + 2 x - 15 = 0$
$x^{2} - 8 x - 20 = 0$ $x^{2} - 8 x - 20 = 0$
$D^{2} + 3 D + 2 = 0$ $D^{2} + 3 D + 2 = 0$
$t^{2} + 5 t - 6 = 0$ $t^{2} + 5 t - 6 = 0$
$x^{2} - 5 x + 3 = 0$ $x^{2} - 5 x + 3 = 0$
$x^{2} + 10 x - 4 = 0$ $x^{2} + 10 x - 4 = 0$
$v^{2} = 15 - 2 v$ $v^{2} = 15 - 2 v$
$16 V - 24 = 2 V^{2}$ $16 V - 24 = 2 V^{2}$
$8 s^{2} + 20 s = 12$ $8 s^{2} + 20 s = 12$
$4 x^{2} + x = 3$ $4 x^{2} + x = 3$
$3 y^{2} = 3 y + 2$ $3 y^{2} = 3 y + 2$
$3 x^{2} = 3 - 4 x$ $3 x^{2} = 3 - 4 x$
$z + 2 = 2 z^{2}$ $z + 2 = 2 z^{2}$
$2 + 6 v = 9 v^{2}$ $2 + 6 v = 9 v^{2}$
$30 y^{2} + 23 y - 40 = 0$ $30 y^{2} + 23 y - 40 = 0$
$62 x + 63 = 40 x^{2}$ $62 x + 63 = 40 x^{2}$
$5 t^{2} + 3 = 7 t$ $5 t^{2} + 3 = 7 t$
$2 d (d - 2) = - 7$ $2 d (d - 2) = - 7$
$s^{2} = 9 + s (1 - 2 s)$ $s^{2} = 9 + s (1 - 2 s)$
$20 r^{2} = 20 r + 1$ $20 r^{2} = 20 r + 1$
$25 y^{2} = 81$ $25 y^{2} = 81$
$37 T = T^{2}$ $37 T = T^{2}$
$15 + 4 z = 32 z^{2}$ $15 + 4 z = 32 z^{2}$
$4 x^{2} - 12 x = 7$ $4 x^{2} - 12 x = 7$
$x^{2} - 0.20 x - 0.40 = 0$ $x^{2} - 0.20 x - 0.40 = 0$
$3.2 x^{2} = 2.5 x + 7.6$ $3.2 x^{2} = 2.5 x + 7.6$
$0.29 Z^{2} - 0.18 = 0.63 Z$ $0.29 Z^{2} - 0.18 = 0.63 Z$
$13.2 x = 15.5 - 12.5 x^{2}$ $13.2 x = 15.5 - 12.5 x^{2}$
$x^{2} + 2 c x - 1 = 0$ $x^{2} + 2 c x - 1 = 0$
$x^{2} - 7 x + (6 + a) = 0$ $x^{2} - 7 x + (6 + a) = 0$
$b^{2} x^{2} + 1 - a = (b + 1) x$ $b^{2} x^{2} + 1 - a = (b + 1) x$
$c^{2} x^{2} - x - 1 = x^{2}$ $c^{2} x^{2} - x - 1 = x^{2}$

In Exercises 35–38, without solving the given equations, determine the character of the roots.

$2 x^{2} - 7 x = - 8$ $2 x^{2} - 7 x = - 8$
$3 x^{2} = 14 - 19 x$ $3 x^{2} = 14 - 19 x$
$3.6 t^{2} + 2.1 = 7.7 t$ $3.6 t^{2} + 2.1 = 7.7 t$
$0.45 s^{2} + 0.33 = 0.12 s$ $0.45 s^{2} + 0.33 = 0.12 s$

In Exercises 39–62, solve the given problems. All numbers are accurate to at least two significant digits.

Find k if the equation $x^{2} + 4 x + k = 0$ $x^{2} + 4 x + k = 0$ has a real double root.
Find the smallest positive integer value of k if the equation $x^{2} + 3 x + k = 0$ $x^{2} + 3 x + k = 0$ has roots with imaginary numbers.
Solve the equation $x^{4} - 5 x^{2} + 4 = 0$ $x^{4} - 5 x^{2} + 4 = 0$ for x. [Hint: The equation can be written as ${(x^{2})}^{2} - 5 (x^{2}) + 4 = 0.$ ${(x^{2})}^{2} - 5 (x^{2}) + 4 = 0.$ First solve for $x^{2} .$ $x^{2} .$ ]
Without drawing the graph or completely solving the equation, explain how to find the number of x-intercepts of a quadratic function.
Use the discriminant $b^{2} - 4 a c$ $b^{2} - 4 a c$ to determine if the equation $90 x^{2} - 123 x + 40 = 0$ $90 x^{2} - 123 x + 40 = 0$ can be solved by factoring. Explain why or why not. Do not solve.
Solve $6 x^{2} - x = 15$ $6 x^{2} - x = 15$ for x by (a) factoring, (b) completing the square, and (c) the quadratic formula. Which is (a) longest? (b) shortest?
In machine design, in finding the outside diameter $D_{0}$ $D_{0}$ of a hollow shaft, the equation $D_{0}^{2} - D D_{0} - 0.25 D^{2} = 0$ $D_{0}^{2} - D D_{0} - 0.25 D^{2} = 0$ is used. Solve for $D_{0}$ $D_{0}$ if $D = 3.625 cm .$ $D = 3.625 cm .$
A missile is fired vertically into the air. The distance s (in ft) above the ground as a function of time t (in s) is given by $s = 300 + 500 t - 16 t^{2} .$ $s = 300 + 500 t - 16 t^{2} .$ (a) When will the missile hit the ground? (b) When will the missile be 1000 ft above the ground?
In analyzing the deflection of a certain beam, the equation $8 x^{2} - 15 L x + 6 L^{2} =^{} 0$ $8 x^{2} - 15 L x + 6 L^{2} =^{} 0$ is used. Solve for x, if $x < L .$ $x < L .$
A homeowner wants to build a rectangular patio with an area of $20.0 m^{2},$ $20.0 m^{2},$ such that the length is 2.0 m more than the width. What should the dimensions be?
Two cars leave an intersection at the same time, one going due east and the other due south. After one has gone 2.0 km farther than the other, they are 6.0 km apart on a direct line. How far did each go?
A student cycled 3.0 km/h faster to college than when returning, which took 15 min longer. If the college is 4.0 km from home, what were the speeds to and from college?
For a rectangle, if the ratio of the length to the width equals the ratio of the length plus the width to the length, the ratio is called the golden ratio. Find the value of the golden ratio, which the ancient Greeks thought had the most pleasing properties to look at.
When focusing a camera, the distance r the lens must move from the infinity setting is given by $r = f^{2} / (p - f),$ $r = f^{2} / (p - f),$ where p is the distance from the object to the lens, and f is the focal length of the lens. Solve for f.
In calculating the current in an electric circuit with an inductance L, a resistance R, and a capacitance C, it is necessary to solve the equation $L m^{2} + R m + 1 / C = 0.$ $L m^{2} + R m + 1 / C = 0.$ Solve for m in the terms of L, R, and C. See Fig. 7.7.

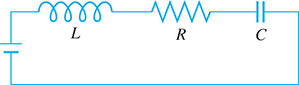
Fig. 7.7
In finding the radius r of a circular arch of height h and span b, we use the formula shown below. Solve for h.

$r = \frac{b^{2} + 4 h^{2}}{8 h}$ $r = \frac{b^{2} + 4 h^{2}}{8 h}$
A computer monitor has a viewing screen that is 33.8 cm wide and 27.3 cm high, with a uniform edge around it. If the edge covers 20.0% of the monitor front, what is the width of the edge?
An investment of $2000 is deposited at a certain annual interest rate. One year later, $3000 is deposited in another account at the same rate. At the end of the second year, the accounts have a total value of $5319.05. The interest rate r can be found by solving $2000 {(1 + r)}^{2} + 3000 (1 + r) = $5319.05.$ $2000 {(1 + r)}^{2} + 3000 (1 + r) = $5319.05.$ What is the interest rate?
In remodeling a house, an architect finds that by adding the same amount to each dimension of a 12-ft by 16-ft rectangular room, the area would be increased by ${80 ft}^{2} .$ ${80 ft}^{2} .$ How much must be added to each dimension?
Two pipes together drain a wastewater-holding tank in 6.00 h. If used alone to empty the tank, one takes 2.00 h longer than the other. How long does each take to empty the tank if used alone?
In order to have the proper strength, the angle iron shown in Fig. 7.8 must have a cross-sectional area of $53.5 {cm}^{2} .$ $53.5 {cm}^{2} .$ Find the required thickness x.

Fig. 7.8
For an optical lens, the sum of the reciprocals of p, the distance of the object from the lens, and q, the distance of the image from the lens, equals the reciprocal of f, the focal length of the lens. If p is 5.0 cm greater than $q (q > 0)$ $q (q > 0)$ and $f = 4.0 cm,$ $f = 4.0 cm,$ find p and q.
The length of a tennis court is 12.8 m more than its width. If the area of the tennis court is $262 m^{2},$ $262 m^{2},$ what are its dimensions? See Fig. 7.9.

Fig. 7.9
Two circular oil spills are tangent to each other. If the distance between centers is 800 m and they cover a combined area of $1.02 \times 10^{6} m^{2},$ $1.02 \times 10^{6} m^{2},$ what is the radius of each? See Fig. 7.10.

Fig. 7.10

Answer to Practice Exercise

$x = \frac{- 1 \pm \sqrt{61}}{6}$ $x = \frac{- 1 \pm \sqrt{61}}{6}$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 7.3 The Quadratic Formula

Create new playlist

Sign In

Sign Up

Table of Contents for
7.3 The Quadratic Formula