Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

20.2 The Sum and Difference Formulas

Formulas for sin( α + β) $\sin (α + β)$ and cos( α + β) $\cos (α + β)$ • Formulas for sin( α − β) $\sin (α - β)$ and cos( α − β) $\cos (α - β)$ • Formulas for tan( α + β) $\tan (α + β)$ and tan( α − β) $\tan (α - β)$

There are other important relations among the trigonometric functions. The most important and useful relations are those that involve twice an angle and half an angle. To obtain these relations, in this section, we derive the expressions for the sine and cosine of the sum and difference of two angles. These expressions will lead directly to the desired relations of double and half angles that we will derive in the following sections.

Equation (12.13), shown in the margin, gives the polar (or trigonometric) form of the product of two complex numbers. We can use this formula to derive the expressions for the sine and cosine of the sum and difference of two angles.

Using Eq. (12.13) to find the product of the complex numbers cos α + j sin α $\cos α + j \sin α$ and cos β + j sin β , $\cos β + j \sin β,$ which are represented in Fig. 20.6, we have

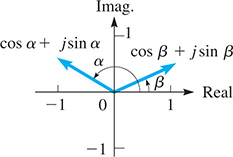
Position vector cosine of beta plus j times sine of beta rises in quadrant 1 at counterclockwise angle beta; position vector cosine of alpha plus j times sine of alpha rises in quadrant 2 at counterclockwise angle alpha. — Fig. 20.6

(cos α + j sin α) (cos β + j sin β) = cos (α + β) + j sin (α + β)

$(\cos α + j \sin α) (\cos β + j \sin β) = \cos (α + β) + j \sin (α + β)$

Expanding the left side, and then switching sides, we have

cos (α + β) + j sin (α + β) = (cos α cos β - sin α sin β) + j (sin α cos β + cos α sin β)

$\cos (α + β) + j \sin (α + β) = (\cos α \cos β - \sin α \sin β) + j (\sin α \cos β + \cos α \sin β)$

Because two complex numbers are equal if their real parts are equal and their imaginary parts are equal, we have the following formulas:

sin (α + β) = sin α cos β + cos α sin β

$\sin (α + β) = \sin α \cos β + \cos α \sin β$ (20.9)

cos (α + β) = cos α cos β - sin α sin β

$\cos (α + β) = \cos α \cos β - \sin α \sin β$ (20.10)

EXAMPLE 1 Verifying the sin(`α` + `β`) formula

Verify that sin 90 ° = 1 , $\sin 90 ° = 1,$ by finding sin(60 ° + 30 ° ) . $\sin (60 ° + 30 °) .$

sin 90 ° = = = sin (60 ° + 30 °) = sin 60 ° cos 30 ° + cos 60 ° sin 30 ° 3 - \sqrt 2 \times 3 - \sqrt 2 + 1 2 \times 1 2 3 4 + 1 4 = 1 using Eq . (20.9) for values, see Section 4.3

$\begin{array}{rcll} \sin 90 ° & = & \sin (60 ° + 30 °) = \sin 60 ° \cos 30 ° + \cos 60 ° \sin 30 ° & using Eq . (20.9) \\ = & \frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2} + \frac{1}{2} \times \frac{1}{2} & \begin{array}{l} for values, see \\ Section 4.3 \end{array} \\ = & \frac{3}{4} + \frac{1}{4} = 1 \end{array}$

CAUTION

It should be obvious from this example that sin(α + β) $\sin (α + β)$ is not equal to sin α + sin β . $\sin α + \sin β .$ If we used such a formula, we would get sin 90 ° = 123–√ + 12 = 1.366 $\sin 90 ° = \frac{1}{2} \sqrt{3} + \frac{1}{2} = 1.366$ for the combination (60 ° + 30 ° ) . $(60 ° + 30 °) .$ This is not possible, because the values of the sine function never exceed 1 in value.

EXAMPLE 2 Using cos(`α` + `β`) with numerical values

Given that sin α = 513 $\sin α = \frac{5}{13}$ (α $α$ in the first quadrant) and sin β = − 35 $\sin β = - \frac{3}{5}$ (for β $β$ in the third quadrant), find cos(α + β) . $\cos (α + β) .$

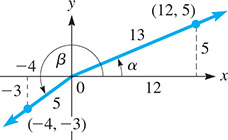
Because sin α = 513 $\sin α = \frac{5}{13}$ for α $α$ in the first quadrant, from Fig. 20.7, we have cos α = 1213 . $\cos α = \frac{12}{13} .$ Also, because sin β = − 35 $\sin β = - \frac{3}{5}$ for β $β$ in the third quadrant, from Fig. 20.7, we also have cos β = − 45 . $\cos β = - \frac{4}{5} .$

Figure 20.7 Full Alternative Text

Then, by using Eq. (20.10), we have

cos (α + β) = = = cos α cos β - sin α sin β 12 13 (- 4 5) - 5 13 (- 3 5) - 48 65 + 15 65 = - 33 65

$\begin{array}{rcl} \cos (α + β) & = & \cos α \cos β - \sin α \sin β \\ = & \frac{12}{13} (- \frac{4}{5}) - \frac{5}{13} (- \frac{3}{5}) \\ = & - \frac{48}{65} + \frac{15}{65} = - \frac{33}{65} \end{array}$

From Eqs. (20.9) and (20.10), we can easily find expressions for sin(α − β) $\sin (α - β)$ and cos(α − β) . $\cos (α - β) .$ This is done by finding sin[ α + ( − β)] $\sin [α + (- β)]$ and cos[ α + ( − β)] . $\cos [α + (- β)] .$ Thus, we have

sin (α - β) = sin [α + (- β)] = sin α cos (- β) + cos α sin (- β)

$\sin (α - β) = \sin [α + (- β)] = \sin α \cos (- β) + \cos α \sin (- β)$

Because cos( − β) = cos β $\cos (- β) = \cos β$ and sin( − β) = − sin β $\sin (- β) = - \sin β$ [see Eq. (8.5) on page 247], we have

sin (α - β) = sin α cos β - cos α sin β

$\sin (α - β) = \sin α \cos β - \cos α \sin β$ (20.11)

In the same manner, we find that

cos (α - β) = cos α cos β + sin α sin β

$\cos (α - β) = \cos α \cos β + \sin α \sin β$ (20.12)

EXAMPLE 3 Using cos(`α` − `β`) formula

Find cos 15 ° $\cos 15 °$ from cos(45 ° − 30 ° ) . $\cos (45 ° - 30 °) .$

cos 15 ° = = = cos (45 ° - 30 °) = cos 45 ° cos 30 ° + sin 45 ° sin 30 ° 2 - \sqrt 2 \times 3 - \sqrt 2 + 2 - \sqrt 2 \times 1 2 = 6 - \sqrt + 2 - \sqrt 4 0.9659 using Eq . (20.12) (exact)

$\begin{array}{rcll} \cos 15 ° & = & \cos (45 ° - 30 °) = \cos 45 ° \cos 30 ° + \sin 45 ° \sin 30 ° & using Eq . (20.12) \\ = & \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \times \frac{1}{2} = \frac{\sqrt{6} + \sqrt{2}}{4} & (exact) \\ = & 0.9659 \end{array}$

EXAMPLE 4 sin(`α` − `β`) formula—oscillating spring

In analyzing the motion of an object oscillating up and down at the end of a spring, the expression sin(ωt + α) cos α − cos(ωt + α) sin α $\sin (ω t + α) \cos α - \cos (ω t + α) \sin α$ occurs. Simplify this expression.

If we let x = ωt + α , $x = ω t + α,$ the expression becomes sin x cos α − cos x sin α , $\sin x \cos α - \cos x \sin α,$ which is the form for sin(x − α) . $\sin (x - α) .$ Therefore,

sin (ω t + α) cos α - cos (ω t + α) sin α = = sin x cos α - cos x sin α = sin (x - α) sin (ω t + α - α) = sin ω t

$\begin{array}{rcl} \sin (ω t + α) \cos α - \cos (ω t + α) \sin α & = & \sin x \cos α - \cos x \sin α = \sin (x - α) \\ = & \sin (ω t + α - α) = \sin ω t \end{array}$

EXAMPLE 5 Using cos(`α` + `β`) formula

Evaluate cos 23 ° cos 67 ° − sin 23 ° sin 67 ° . $\cos 23 ° \cos 67 ° - \sin 23 ° \sin 67 ° .$

We note that this expression fits the form of the right side of Eq. (20.10), so

cos 23 ° cos 67 ° - sin 23 ° sin 67 ° = = = cos (23 ° + 67 °) cos 90 ° 0

$\begin{array}{rcl} \cos 23 ° \cos 67 ° - \sin 23 ° \sin 67 ° & = & \cos (23 ° + 67 °) \\ = & \cos 90 ° \\ = & 0 \end{array}$

Again, we are able to evaluate this expression by recognizing the form of the given expression. Evaluation by a calculator will verify the result.

By dividing the right side of Eq. (20.9) by that of Eq. (20.10), we can determine expressions for tan(α + β) , $\tan (α + β),$ and by dividing the right side of Eq. (20.11) by that of Eq. (20.12), we can determine an expression for tan(α − β) . $\tan (α - β) .$ The derivation of these formulas is Exercise 33 of this section. These formulas can be written together, as

tan (α \pm β) = tan α \pm tan β 1 \mp tan α tan β

$\tan (α \pm β) = \frac{\tan α \pm \tan β}{1 \mp \tan α \tan β}$ (20.13)

The formula for tan(α + β) $\tan (α + β)$ uses the upper signs, and the formula for tan(α − β) $\tan (α - β)$ uses the lower signs.

Certain trigonometric identities can be proven by the formulas derived in this section. The following examples illustrate this use of these formulas.

EXAMPLE 6 Sin(`α` + `β`)—calculator verification

Prove that sin(180 ° + x) = − sin x . $\sin (180 ° + x) = - \sin x .$

sin (180 ° + x) = = = sin 180 ° cos x + cos 180 ° sin x using Eq . (20.9) (0) cos x + (- 1) sin x sin 180 ° = 0, cos 180 ° = - 1 - sin x

$\begin{array}{rcl} \sin (180 ° + x) & = & \sin 180 ° \cos x + \cos 180 ° \sin x using Eq . (20.9) \\ = & (0) \cos x + (- 1) \sin x \sin 180 ° = 0, \cos 180 ° = - 1 \\ = & - \sin x \end{array}$

Although x may or may not be an acute angle, this agrees with the results for the sine of a third-quadrant angle as discussed in Section 8.2. See Fig. 20.8. The calculator check of this identity, with y1 = sin(π + x) $y_{1} = \sin (π + x)$ and y2 = − sin x $y_{2} = - \sin x$ is shown in Fig. 20.9. This screen was captured while y2 $y_{2}$ (in red) was being graphed right over y1 $y_{1}$ (in blue).

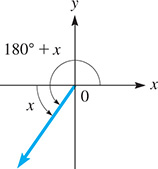
The terminal side of a standard angle is a counterclockwise angle 180 degrees plus x; from the negative x-axis to the side is counterclockwise angle x. — Fig. 20.8

A curve oscillates about y = 0 with amplitude 1, period 2 pi, and maximum (negative pi over 2, 1). — Fig. 20.9

EXAMPLE 7 Proving a trig identity with tan(`α` ± `β`)

Show that tan(α + β) tan(α − β) = tan2 α − tan2 β1 − tan2 αtan2 β . $\tan (α + β) \tan (α - β) = \frac{\tan^{2} α - \tan^{2} β}{1 - \tan^{2} α \tan^{2} β} .$

Using both of Eqs. (20.13), we have

tan (α + β) tan (α - β) = = (tan α + tan β 1 - tan α tan β) (tan α - tan β 1 + tan α tan β) tan 2 α - tan 2 β 1 - tan 2 α tan 2 β

$\begin{array}{rcl} \tan (α + β) \tan (α - β) & = & (\frac{\tan α + \tan β}{1 - \tan α \tan β}) (\frac{\tan α - \tan β}{1 + \tan α \tan β}) \\ = & \frac{\tan^{2} α - \tan^{2} β}{1 - \tan^{2} α \tan^{2} β} \end{array}$

EXAMPLE 8 Trig identity using sin(`α` − `β`)

Simplify the expression sin(α − β)sin α sin β . $\frac{\sin (α - β)}{\sin α \sin β} .$

sin ( α - β ) sin α sin β = = = sin α cos β - cos α sin β sin α sin β sin α cos β sin α sin β - cos α sin β sin α sin β = cos β sin β - cot β - cot α using Eq . (20.11) cos α sin α using Eq . (20.5)

$\begin{array}{rcll} \frac{\sin (α - β)}{\sin α \sin β} & = & \frac{\sin α \cos β - \cos α \sin β}{\sin α \sin β} & using Eq . (20.11) \\ = & \frac{\sin α \cos β}{\sin α \sin β} - \frac{\cos α \sin β}{\sin α \sin β} = \frac{\cos β}{\sin β} - & \frac{\cos α}{\sin α} \\ = & \cot β - \cot α & using Eq . (20.5) \end{array}$

EXAMPLE 9 Using sin(`α` − `β`)—three-phase generator

Alternating electric current is produced essentially by a coil of wire rotating in a magnetic field, and this is the basis for designing generators of alternating current. A three-phase generator uses three coils of wire and thereby produces three electric currents at the same time. This is the most widely used type of polyphase generator as mentioned in the chapter introduction on page 535.

The voltages induced in a three-phase generator can be represented as

E 1 = E 0 sin ω t E 2 = E 0 sin (ω t - 2 π 3) E 3 = E 0 sin (ω t - 4 π 3)

$E_{1} = E_{0} \sin ω t E_{2} = E_{0} \sin (ω t - \frac{2 π}{3}) E_{3} = E_{0} \sin (ω t - \frac{4 π}{3})$

where E0 $E_{0}$ is the maximum voltage and ω $ω$ is the angular velocity of rotation. Show that the sum of these voltages at any time t is zero.

Setting up the sum E1 + E2 + E3 $E_{1} + E_{2} + E_{3}$ and using Eq. (20.11), we have

E 1 + E 2 + E 3 = E 0 [sin ω t + sin (ω t - 2 π 3) + sin (ω t - 4 π 3)] = E 0 (sin ω t + sin ω t cos 2 π 3 - cos ω t sin 2 π 3 + sin ω t cos 4 π 3 - cos ω t sin 4 π 3) = E 0 [sin ω t + (sin ω t) (- 1 2) - (cos ω t) (1 2 3 - \sqrt) + (sin ω t) (- 1 2) - (cos ω t) (- 1 2 3 - \sqrt)] = E 0 [(sin ω t) (1 - 1 2 - 1 2) + (cos ω t) (1 2 3 - \sqrt - 1 2 3 - \sqrt)] = 0

$\begin{array}{l} E_{1} + E_{2} + E_{3} \\ = E_{0} [\sin ω t + \sin (ω t - \frac{2 π}{3}) + \sin (ω t - \frac{4 π}{3})] \\ = E_{0} (\sin ω t + \sin ω t \cos \frac{2 π}{3} - \cos ω t \sin \frac{2 π}{3} + \sin ω t \cos \frac{4 π}{3} - \cos ω t \sin \frac{4 π}{3}) \\ = E_{0} [\sin ω t + (\sin ω t) (- \frac{1}{2}) - (\cos ω t) (\frac{1}{2} \sqrt{3}) + (\sin ω t) (- \frac{1}{2}) - (\cos ω t) (- \frac{1}{2} \sqrt{3})] \\ = E_{0} [(\sin ω t) (1 - \frac{1}{2} - \frac{1}{2}) + (\cos ω t) (\frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{3})] = 0 \end{array}$

To show that E1 + E2 + E3 = 0 $E_{1} + E_{2} + E_{3} = 0$ on a calculator, in Fig. 20.10 we let y1 = sin x , y2 = sin(x − 2π / 3) , y3 = sin(x − 4π / 3) , $y_{1} = \sin x, y_{2} = \sin (x - 2 π / 3), y_{3} = \sin (x - 4 π / 3),$ and y4 = y1 + y2 + y3 . $y_{4} = y_{1} + y_{2} + y_{3} .$ In Fig. 20.11, y1 , y2 , $y_{1}, y_{2},$ and y3 $y_{3}$ are the three sine curves, and y4 $y_{4}$ is the pink line along the x-axis that shows y1 + y2 + y3 = 0 . $y_{1} + y_{2} + y_{3} = 0 .$ This shows us that the sum of the three voltages is zero at any point in time.

Figure 20.10 Full Alternative Text

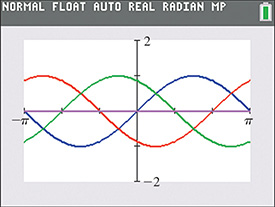
Three curves oscillate about y = 0 with amplitudes 1 and periods 3. Maximums and minimums are different for each. — Fig. 20.11

EXERCISES 20.2

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the given problems.

In Example 2, change 513 $\frac{5}{13}$ to 1213 $\frac{12}{13}$ and then find the value of cos(α + β) . $\cos (α + β) .$
In Example 6, change 180 ° + x $180 ° + x$ to 180 ° − x $180 ° - x$ and then determine what other changes result.

In Exercises 3–6, determine the values of the given functions as indicated.

Find sin 105 ° $\sin 105 °$ by using 105 ° = 60 ° + 45 ° . $105 ° = 60 ° + 45 ° .$
Find tan 75 ° $\tan 75 °$ by using 75 ° = 30 ° + 45 ° . $75 ° = 30 ° + 45 ° .$
Find cos 15 ° $\cos 15 °$ by using 15 ° = 60 ° − 45 ° . $15 ° = 60 ° - 45 ° .$
Find sin 15 ° $\sin 15 °$ by using 15 ° = 225 ° − 210 ° . $15 ° = 225 ° - 210 ° .$

In Exercises 7–10, evaluate the given functions with the following information: sin α = 4/5 $\sin α = 4/5$ (α $α$ in first quadrant) and cos β = − 12/13 $\cos β = - 12/13$ (β $β$ in second quadrant).

sin(α + β) $\sin (α + β)$
tan(β − α) $\tan (β - α)$
cos(α + β) $\cos (α + β)$
sin(α − β) $\sin (α - β)$

In Exercises 11–20, simplify the given expressions.

sin x cos 2x + sin 2x cos x $\sin x \cos 2 x + \sin 2 x \cos x$
sin 3x cos x − sin x cos 3x $\sin 3 x \cos x - \sin x \cos 3 x$
cos 5x cos x + sin 5x sin x $\cos 5 x \cos x + \sin 5 x \sin x$
tan(x − y) + tan x1 − tan(x − y) tan y $\frac{\tan (x - y) + \tan x}{1 - \tan (x - y) \tan y}$
sin(90 ° − x) $\sin (90 ° - x)$
cos(32 π − x) $\cos (\frac{3}{2} π - x)$
tan(x − π) $\tan (x - π)$
sin(x + π / 2) $\sin (x + π / 2)$
sin 3x cos(3x − π) − cos 3x sin(3x − π) $\sin 3 x \cos (3 x - π) - \cos 3 x \sin (3 x - π)$
cos(x + π) cos(x − π) + sin(x + π) sin(x − π) $\cos (x + π) \cos (x - π) + \sin (x + π) \sin (x - π)$

In Exercises 21–24, evaluate each expression by first changing the form. Verify each by use of a calculator.

sin 122 ° cos 32 ° − cos 122 ° sin 32 ° $\sin 122 ° \cos 32 ° - \cos 122 ° \sin 32 °$
cos 250 ° cos 70 ° + sin 250 ° sin 70 ° $\cos 250 ° \cos 70 ° + \sin 250 ° \sin 70 °$
cosπ5 cos3π10 − sinπ5 sin3π10 $\cos \frac{π}{5} \cos \frac{3 π}{10} - \sin \frac{π}{5} \sin \frac{3 π}{10}$
tanπ10 + tan3π201 − tanπ10 tan3π20 $\frac{\tan \frac{π}{10} + \tan \frac{3 π}{20}}{1 - \tan \frac{π}{10} \tan \frac{3 π}{20}}$

In Exercises 25–28, prove the given identities.

sin(x + y) sin(x − y) = sin2 x − sin2 y $\sin (x + y) \sin (x - y) = \sin^{2} x - \sin^{2} y$
cos(x + y) cos(x − y) = cos2 x − sin2 y $\cos (x + y) \cos (x - y) = \cos^{2} x - \sin^{2} y$
cos(α + β) + cos(α − β) = 2 cos α cos β $\cos (α + β) + \cos (α - β) = 2 \cos α \cos β$
tan(90 ° + x) = − cot x $\tan (90 ° + x) = - \cot x$ [Explain why Eq. (20.13) cannot be used for this, but Eqs. (20.9) and (20.10) can be used.]

In Exercises 29–32, verify each identity by comparing the graph of the left side with the graph of the right side on a calculator.

cos(π6 + x) = 3–√ cos x − sin x2 $\cos (\frac{π}{6} + x) = \frac{\sqrt{3} \cos x - \sin x}{2}$
sin(120 ° − x) = 3–√ cos x + sin x2 $\sin (120 ° - x) = \frac{\sqrt{3} \cos x + \sin x}{2}$
tan(3π4 + x) = tan x − 1tan x + 1 $\tan (\frac{3 π}{4} + x) = \frac{\tan x - 1}{\tan x + 1}$
cos(π2 − x) = sin x $\cos (\frac{π}{2} - x) = \sin x$

In Exercises 33–36, derive the given equations as indicated. Equations (20.14)–(20.16) are known as the product formulas.

By dividing the right side of Eq. (20.9) by that of Eq. (20.10), and dividing the right side of Eq. (20.11) by that of Eq. (20.12), derive Eq. (20.13).

$tan (α \pm β) = tan α \pm tan β 1 \mp tan α tan β$ $\tan (α \pm β) = \frac{\tan α \pm \tan β}{1 \mp \tan α \tan β}$ (20.13)

(Hint: Divide numerator and denominator by cos α cos β . $\cos α \cos β .$ )
By adding Eqs. (20.9) and (20.11), derive the equation

$sin α cos β = 1 2 [sin (α + β) + sin (α - β)]$ $\sin α \cos β = \frac{1}{2} [\sin (α + β) + \sin (α - β)]$ (20.14)
By adding Eqs. (20.10) and (20.12), derive the equation

$cos α cos β = 1 2 [cos (α + β) + cos (α - β)]$ $\cos α \cos β = \frac{1}{2} [\cos (α + β) + \cos (α - β)]$ (20.15)
By subtracting Eq. (20.10) from Eq. (20.12), derive

$sin α sin β = 1 2 [cos (α - β) - cos (α + β)]$ $\sin α \sin β = \frac{1}{2} [\cos (α - β) - \cos (α + β)]$ (20.16)

In Exercises 37–40, derive the given equations by letting α + β = x $α + β = x$ and α − β = y , $α - β = y,$ which leads to α = 12 (x + y) $α = \frac{1}{2} (x + y)$ and β = 12 (x − y) . $β = \frac{1}{2} (x - y) .$ The resulting equations are known as the factor formulas.

Use Eq. (20.14) and the substitutions above to derive the equation

$sin x + sin y = 2 sin 1 2 (x + y) cos 1 2 (x - y)$ $\sin x + \sin y = 2 \sin \frac{1}{2} (x + y) \cos \frac{1}{2} (x - y)$ (20.17)
Use Eqs. (20.9) and (20.11) and the substitutions above to derive the equation

$sin x - sin y = 2 sin 1 2 (x - y) cos 1 2 (x + y)$ $\sin x - \sin y = 2 \sin \frac{1}{2} (x - y) \cos \frac{1}{2} (x + y)$ (20.18)
Use Eq. (20.15) and the substitutions above to derive the equation

$cos x + cos y = 2 cos 1 2 (x + y) cos 1 2 (x - y)$ $\cos x + \cos y = 2 \cos \frac{1}{2} (x + y) \cos \frac{1}{2} (x - y)$ (20.19)
Use Eq. (20.16) and the substitutions above to derive the equation

$cos x - cos y = - 2 sin 1 2 (x + y) sin 1 2 (x - y)$ $\cos x - \cos y = - 2 \sin \frac{1}{2} (x + y) \sin \frac{1}{2} (x - y)$ (20.20)

In Exercises 41–54, solve the given problems.

Evaluate exactly: sin(x + 30 ° ) cos x − cos(x + 30 ° ) sin x $\sin (x + 30 °) \cos x - \cos (x + 30 °) \sin x$
Simplify: sin(π6 − θ) + cos(π3 − θ) $\sin (\frac{π}{6} - θ) + \cos (\frac{π}{3} - θ)$
Show that sin 2xsin x = 2 cos x . $\frac{\sin 2 x}{\sin x} = 2 \cos x .$ [Hint: sin 2x = sin(x + x) . $\sin 2 x = \sin (x + x) .$ ]
Using graphs displayed on a calculator, verify the identity in Exercise 43.
Explain how the exact value of sin 75 ° $\sin 75 °$ can be found using either Eq. (20.9) or Eq. (20.11).
A vertical pole of length L is placed on top of a hill of height h. From the plain below the angles of elevation of the top and bottom of the pole are α $α$ and β . $β .$ See Fig. 20.12. Show that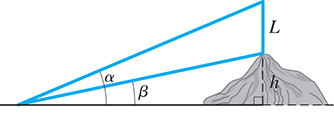

Fig. 20.12

$h = L cos α sin β sin ( α - β )$ $h = \frac{L \cos α \sin β}{\sin (α - β)}$
The design of a certain three-phase alternating-current generator uses the fact that the sum of the currents Icos(θ + 30 ° ) , Icos(θ + 150 ° ) , $I \cos (θ + 30 °), I \cos (θ + 150 °),$ and Icos(θ + 270 ° ) $I \cos (θ + 270 °)$ is zero. Verify this.
The current (in A) in a certain AC circuit is given by i = 4 sin(120πt + π2) . $i = 4 \sin (120 π t + \frac{π}{2}) .$ Use the sum formula for sine to write this in a different form and then simplify.
For voltages V1 = 20 sin 120πt $V_{1} = 20 \sin 120 π t$ and V2 = 20 cos 120πt , $V_{2} = 20 \cos 120 π t,$ show that V = V1 + V2 = 202–√ sin(120πt + π / 4) . $V = V_{1} + V_{2} = 20 \sqrt{2} \sin (120 π t + π / 4) .$ Use a calculator to verify this result.
The displacements y1 $y_{1}$ and y2 $y_{2}$ of two waves traveling through the same medium are given by y1 = Asin 2π(t / T − x / λ) $y_{1} = A \sin 2 π (t / T - x / λ)$ and y2 = Asin 2π(t / T + x / λ) . $y_{2} = A \sin 2 π (t / T + x / λ) .$ Find an expression for the displacement y1 + y2 $y_{1} + y_{2}$ of the combination of the waves.
The displacement d of a water wave is given by the equation d = d0sin(ωt + α) . $d = d_{0} \sin (ω t + α) .$ Show that this can be written as d = d1sin ωt + d2cos ωt , $d = d_{1} \sin ω t + d_{2} \cos ω t,$ where d1 = d0cos α $d_{1} = d_{0} \cos α$ and d2 = d0sin α . $d_{2} = d_{0} \sin α .$
A weight w is held in equilibrium by forces F and T as shown in Fig. 20.13. Equations relating w, F, and T are

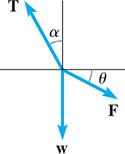
Fig. 20.13

$F cos θ w + F sin θ Show that w = = = T sin α T cos α T cos ( θ + a ) cos θ .$ $\begin{array}{rcl} F \cos θ & = & T \sin α \\ w + F \sin θ & = & T \cos α \\ Show that w & = & \frac{T \cos (θ + a)}{\cos θ} . \end{array}$
For the two bevel gears shown in Fig. 20.14, the equation tan α = sin βR + cos βis used . $\tan α = \frac{\sin β}{R + \cos β} is used .$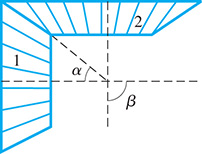

Fig. 20.14

Here, R is the ratio of gear 1 to gear 2. Show that

R = sin(β − α)sin α . $R = \frac{\sin (β - α)}{\sin α} .$
In the analysis of the angles of incidence i and reflection r of a light ray subject to certain conditions, the following expression is found:

E2(tan rtan i + 1) = E1(tan rtan i − 1)Show that E2 = E1 sin(r − i)sin(r + i) . $\begin{array}{l} E_{2} (\frac{\tan r}{\tan i} + 1) = E_{1} (\frac{\tan r}{\tan i} - 1) \\ {Show that E}_{2} = E_{1} \frac{\sin (r - i)}{\sin (r + i)} . \end{array}$

Answers to Practice Exercises

1
tan x

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 20.2 The Sum and Difference Formulas

Create new playlist

Sign In

Sign Up

Table of Contents for
20.2 The Sum and Difference Formulas