16.2 Multiplication of Matrices

  • Multiplication of Matrices • Identity Matrix • Inverse of a Matrix

The definition for the multiplication of matrices does not have an intuitive basis. However, through the solution of a system of linear equations we can, at least in part, show why multiplication is defined as it is. Consider Example 1.

EXAMPLE 1 Reasoning for definition of multiplication

If we solve the system of equations

2x + y = 17x + 3y = 5

we get x = 2 , y =  − 3. Checking this solution in each of the equations, we get

2(2) + 1( − 3) = 17(2) + 3( − 3) = 5

Let us represent the coefficients of the equations by the matrix  [ 2173 ]  and the solutions by the matrix  [ 2 − 3 ]  .  If we now indicate the multiplications of these matrices and perform it as shown

 [ 2173 ]  [ 2 − 3 ]  =  [ 2(2) + 1( − 3)7(2) + 3( − 3) ]  =  [ 15 ] 

we note that we obtain a matrix that properly represents the right-side values of the equations. (Note the products and sums in the resulting matrix.)

Following reasons along the lines indicated in Example 1, we now define the multiplication of matrices. If the number of columns in a first matrix equals the number of rows in a second matrix, the product of these matrices is formed as follows: The element in a specified row and a specified column of the product matrix is the sum of the products formed by multiplying each element in the specified row of the first matrix by the corresponding element in the specific column of the second matrix. The product matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix. Consider the following examples.

EXAMPLE 2 Multiplying matrices

Find the product AB, where

A =  [ 21 − 3012 ]  B =  [  − 165 − 2301 − 4 ] 

With two columns in matrix A and two rows in matrix B, the product can be formed. The element in the first row and first column of the product is the sum of the products of the corresponding elements of the first row of A and first column of B. The elements in the first row and second column of the product is the sum of the products of corresponding elements of the first row of A and second column of B. We continue until we have three rows (the number in A) and four columns (the number in B).

Multiplying matrices.

The elements used to form the element in the first row and first column and the element in the third row and second column of the product are outlined in color. Figure 16.4 shows the calculator display for the matrix product AB.

A calculator screen.

Fig. 16.4

Graphing calculator keystrokes: bit.ly/2RLwgqM

In trying to form the product BA, we see that B has four columns and A has three rows. Because these numbers are not the same, the product cannot be formed.

CAUTION

Therefore, AB ≠ BA ,  which means matrix multiplication is not commutative (except in special cases), and therefore differs from multiplication of real numbers.

EXAMPLE 3

The product of two matrices below may be formed because the first matrix has four columns and the second matrix has four rows. The matrix is formed as shown.

 [  − 193 − 220 − 71 ]  [ 6 − 2103 − 539 ]  =  [  − 1(6) + 9(1) + 3(3) + ( − 2)(3) − 1( − 2) + 9(0) + 3( − 5) + ( − 2)(9)2(6) + 0(1) + ( − 7)(3) + 1(3)2( − 2) + 0(0) + ( − 7)( − 5) + 1(9) ]  =  [  − 6 + 9 + 9 − 62 + 0 − 15 − 1812 + 0 − 21 + 3 − 4 + 0 + 35 + 9 ]  =  [ 6 − 31 − 640 ] 

IDENTITY MATRIX

There are two special matrices of particular importance in the multiplication of matrices. The first of these is the identity matrix I, which is a square matrix with 1’s for elements of the principal diagonal with all other elements zero. (The principal diagonal starts with the element a11 . ) It has the property that if it is multiplied by another square matrix with the same number of rows and columns, then the second matrix equals the product matrix.

EXAMPLE 4 Identity matrix

Show that AI = IA = A for the matrix

A =  [ 2 − 341 ] 

Because A has two rows and two columns, we choose I with two rows and two columns. Therefore, for this case

I =  [ 1001 ] ← elements of principal diagonal are 1' s

Forming the indicated products, we have results as follows:

AI =  [ 2 − 341 ]  [ 1001 ]  =  [ 2(1) + ( − 3)(0)2(0) + ( − 3)(1)4(1) + 1(0)4(0) + 1(1) ]  =  [ 2 − 341 ] IA =  [ 1001 ]  [ 2 − 341 ]  =  [ 1(2) + 0(4)1( − 3) + 0(1)0(2) + 1(4)0( − 3) + 1(1) ]  =  [ 2 − 341 ] 

Therefore, we see that AI = IA = A . 

INVERSE OF A MATRIX

For a given square matrix A, its inverse A − 1 is the other important special matrix. The matrix A and its inverse A − 1 have the property that

AA − 1 = A − 1A = I
(16.5)

If the product of two square matrices equals the identity matrix, the matrices are called inverses of each other. In the next section, we develop the procedure for finding the inverse of a square matrix, and the section that follows shows how the inverse is used in the solution of systems of equations. At this point, we simply show that the product of certain matrices equals the identity matrix and that therefore these matrices are inverses of each other.

CAUTION

Only square matrices can have inverses, and if the determinant of a matrix is zero, then the inverse does not exist.

EXAMPLE 5 Inverse matrix

For the given matrices A and B, show that AB = BA = I ,  and therefore that B = A − 1 . 

A =  [ 1 − 3 − 27 ] B =  [ 7321 ] 

Forming the products AB and BA, we have the following:

AB =  [ 1 − 3 − 27 ]  [ 7321 ]  =  [ 7 − 63 − 3 − 14 + 14 − 6 + 7 ]  =  [ 1001 ] BA =  [ 7321 ]  [ 1 − 3 − 27 ]  =  [ 7 − 6 − 21 + 212 − 2 − 6 + 7 ]  =  [ 1001 ] 

Since AB = I and BA = I , B = A − 1 and A = B − 1 . 

EXAMPLE 6 Matrix multiplication—transmission production

A company makes three types of automobile transmissions: 4-gear manual (type X), 4-gear automatic (type Y), and 5-gear automatic (type Z). In one day, it produces 40 of type X, 50 of type Y, and 80 of type Z. Required for production are 4 units of parts (some preassembled) and 1 worker-hour for type X, 5 units of parts and 2 worker-hours for type Y, and 3 units of parts and 2 worker-hours for type Z. Letting matrix A represent the number of each type produced, and matrix B represent the parts and time requirements, we have

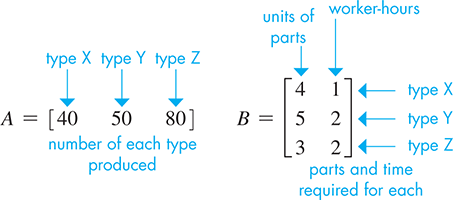
Two matrices A and B, A is a 1 by 3 matrix and B is a 3 by 2 matrix.

The product AB gives the total number of units of parts and the total number of worker-hours needed for the day’s production in a one-row, two-column matrix:

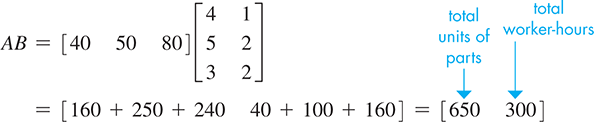
The processes for multiplying Matrix A by Matrix B.

Therefore, 650 units of parts and 300 worker-hours are required.

We have seen that matrix multiplication is not commutative (see Example 2); that is, AB ≠ BA in general. This differs from the multiplication of real numbers. Another difference is that it is possible that AB = O ,  even though neither A nor B is O. There are also some similarities. For example, AI = A ,  where I and the number 1 are analogous. Also, the distributive property A(B + C) = AB + AC holds for matrix multiplication.

EXERCISES 16.2

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then perform the indicated multiplications.

  1. In Example 2, interchange columns 1 and 2 in matrix A and then do the multiplication.

  2. In Example 5, in A change  − 2 to 2 and  − 3 to 3, in B change 2 to  − 2 and 3 to  − 3 ,  and then do the multiplications.

In Exercises 3–10, perform the indicated multiplications.

  1.  [ 4 − 2 ]  [  − 1026 ] 

  2.  [  − 126 − 23 ]  [ 4813 − 1209 ] 

  3.  [ 9 − 13702 ]  [ 40 − 1520 ] 

  4.  [ 0 − 124112 ]  [ 3 − 11261 ] 

  5.  [  − 83213 − 628 ]  [ 2 − 345 ] 

  6.  [ 12 − 4743 − 1836 − 22 ]  [ 12 − 11 ] 

  7.  [  − 173510 − 1 − 512 ]  [ 215 − 3 ] 

  8.  [ 54 ]  [ 4 − 4 − 55 ] 

In Exercises 11–14, use a graphing calculator to perform the indicated multiplications.

  1.  [ 2 − 38 − 1 ]  [ 30 − 17 − 56 ] 

  2.  [  − 7850 ]  [  − 901001040 ] 

  3.  [  − 7.12.30.5 − 3.8 − 2.44.9 ]  [ 6.5 − 5.24.91.7 − 1.86.9 ] 

  4.  [ 12 − 6 − 61 − 24012 ]  [ 1 − 10 − 52 ] 

In Exercises 15–18, find, if possible, AB and BA. If it is not possible, explain why.

  1. A =  [ 1 − 38 ] B =  [  − 157 ] 

  2. A =  [  − 3201 − 45 ] B =  [  − 204 − 65 − 1 ] 

  3. A =  [  − 10254042 − 50 ] B =  [ 6 − 1512 ] 

  4. A =  [  − 2173 − 1002 − 1 ] B =  [ 4 − 15 ] 

In Exercises 19–22, show that AI = IA = A . 

  1. A =  [ 18 − 22 ] 

  2. A =  [  − 1528 − 564 ] 

  3. A =  [ 39 − 158046 − 1224 ] 

  4. A =  [  − 1204 − 31213 ] 

In Exercises 23–26, determine whether or not B = A − 1 . 

  1. A =  [ 5 − 2 − 21 ] B =  [ 1225 ] 

  2. A =  [ 3 − 45 − 7 ] B =  [ 7 − 45 − 2 ] 

  3. A =  [ 1 − 232 − 57 − 13 − 5 ] B =  [ 4 − 113 − 2 − 11 − 1 − 1 ] 

  4. A =  [ 1 − 133 − 48 − 23 − 4 ] B =  [ 8 − 5 − 44 − 2 − 1 − 111 ] 

In Exercises 27–30, determine by matrix multiplication whether or not A is the proper matrix of solution values.

  1. 3x − 2y =  − 14x + y = 6A =  [ 12 ] 

  2. 4x + y =  − 53x + 4y = 8A =  [  − 23 ] 

  3. 3x + y + 2z = 1x − 3y + 4z =  − 32x + 2y + z = 1A =  [  − 121 ] 

  4. 2x − y + z = 7x − 3y + 2z = 73x + y = 7A =  [ 3 − 2 − 1 ] 

In Exercises 31–34, perform the indicated matrix multiplications on a calculator, using the following matrices. For matrix A, A2 = A × A . 

A =  [ 2 − 3 − 5 − 1451 − 3 − 4 ]  B =  [ 1 − 2 − 6 − 32920 − 3 ]  C =  [ 1 − 3 − 4 − 1341 − 3 − 4 ] 

  1. Show that A2 = A . 

  2. Show that C2 = O . 

  3. Show that B3 = B . 

  4. Show that A3B3 = AB . 

In Exercises 35–48, solve the given problems.

  1. For matrices A =  [ abba ]  and B =  [ cddc ]  ,  show that AB = BA . 

  2. For matrix A =  [ 122212221 ]  ,  show that A2 − 4A − 5I = O . 

  3. Using two rows and columns, show that ( − I)2 = I . 

  4. For J =  [ j00j ]  ,  where j =  − 1 ,  show that J2 =  − I , J3 =  − J ,  and J4 = I .  Explain the similarity with j2 , j3 ,  and j4 . 

  5. Show that A2 − I = (A + I)(A − I) for A =  [ 2435 ]  . 

  6. By using A =  [ 0200 ]  ,  B =  [ 3120 ]  ,  C =  [ 6320 ]  ,  show that AB = AC does not necessarily mean that B = C . 

  7. From past records, satellite television Company A finds that among its current customers, 92% will still be a customer one year from now and the remaining 8% will be lost to other competing companies. Also, among customers who are currently with other companies, 14% will switch to Company A within one year and the remaining 86% will remain with other companies. This is represented by the following transition matrix T:

    One year from nowAOtherNowAOther [ 0.920.080.140.86 ]  = T

    Company A currently has 40% of the market share, given by AOther [ 0.400.60 ]  .  Find the market share of Company A after one year by multiplying  [ 0.400.60 ] T . 

  8. In Exercise 41, the market share of Company A in future years can be found by multiplying by the transition matrix T repeatedly. What would the market share of Company A be after 3 years?

  9. In studying the motion of electrons, one of the Pauli spin matrices used is sy =  [ 0 − jj0 ]  ,  where j =  − 1 .  Show that sy2 = I . 

  10. To rotate a set of points (x1 , y1) , (x2 , y2) , (x3 , y3) ,  …  counterclockwise about the origin by angle θ ,  we multiply  [ cosθ − sinθsinθcosθ ]  [ x1x2x3y1y2y3 …  ]  .  If a photo on a computer screen has corners at (4 , 2) , ( − 4 , 2) , ( − 4 ,  − 2) ,  and (4 ,  − 2) ,  find the coordinates of the corners after the photo has been rotated counterclockwise about the origin by 30 ° .

  11. In an ammeter, nearly all the electric current flows through a shunt, and the remaining known fraction of current is measured by the meter. See Fig. 16.5. From the given matrix equation, find voltage v2 and current i2 in terms of v1 , i1 ,  and resistance R, whichever may be applicable.

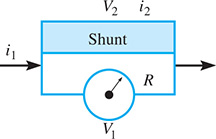
    Current i sub 1 has V sub 2 and i sub 2 pass through a shunt. V sub 1 passes through a meter and resistance R.

    Fig. 16.5

     [ v2i2 ]  =  [ 10 − 1R1 ]  [ v1i1 ] 

  12. In the theory related to the reproduction of color photography, the equation

     [ XYZ ]  =  [ 1.00.100.51.00.10.30.41.0 ]  [ xyz ] 

    is found. The X, Y, and Z represent the red, green, and blue densities of the reproductions, respectively, and the x, y, and z represent the red, green, and blue densities, respectively, of the subject. Give the equations relating X, Y, and Z and x, y, and z.

  13. The path of an Earth satellite can be written as

     [ xy ]  [ 2.76 − 112.81 ]  [ xy ]  = [ 7.76 × 107] 

    where distances are in miles. What type of curve is represented? (See Section 14.1.)

  14. Using Kirchhoff’s laws on the circuit shown in Fig. 16.6, the following matrix equation is found. By matrix multiplication, find the resulting system of equations.

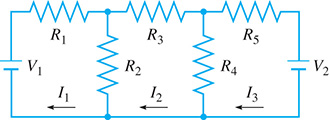
    A circuit.

    Fig. 16.6

     [ R1 + R2 − R20 − R2R2 + R3 + R4 − R40 − R4R4 + R5 ]  [ I1I2I3 ]  =  [ V10 − V2 ] 

Answers to Practice Exercises

  1.  [  − 334354 − 44 − 84120 ] 

  2. 4 rows, 4 columns

  3. AB = BA =  [ 1001 ] 

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.222.240.21