2.4 Circles

  • Properties of Circles • Tangent Secant Lines • Circumference Area • Circular Arcs Angles • Radian Measure of an Angle

The next geometric figure we consider is the circle. All points on a circle are at the same distance from a fixed point, the center of the circle. The distance from the center to a point on the circle is the radius of the circle. The distance between two points on the circle on a line through the center is the diameter. Therefore, the diameter d is twice the radius r, or d = 2r .  See Fig. 2.76.

A diagram of a circle. A line segment that goes from one point on the circle to another point while passing through the center is the diameter. Each half of the diameter is a radius.

Fig. 2.76

There are also certain types of lines associated with a circle. A chord is a line segment having its endpoints on the circle. A tangent is a line that touches (does not pass through) the circle at one point. A secant is a line that passes through two points of the circle. See Fig. 2.77.

A diagram of a circle. A chord goes from one point of the circle to another while staying within the circle. A tangent line passes through one point on the circle. A secant line passes through two points on the circle.

Fig. 2.77

An important property of a tangent is that a tangent is perpendicular to the radius drawn to the point of contact. This is illustrated in the following example.

EXAMPLE 1 Tangent line perpendicular to radius

In Fig. 2.78, O is the center of the circle, AB is tangent at B. If  ∠ OAB = 25 °  ,  find  ∠ AOB . 

A diagram of a circle and angle.

Fig. 2.78

Because the center is O, OB is a radius of the circle. A tangent is perpendicular to a radius at the point of tangency, which means  ∠ ABO = 90 °  so that

 ∠ OAB +  ∠ OBA = 25 °  + 90 °  = 115 ° 

Because the sum of the angles of a triangle is 180 ° , we have

 ∠ AOB = 180 °  − 115 °  = 65 ° 

CIRCUMFERENCE AREA OF A CIRCLE

The perimeter of a circle is called the circumference. The formulas for the circumference area of a circle are as follows:

c = 2πrCircumference of a circle of radius r
(2.9)
A = πr2Area of a circle of radius r
(2.10)

Here, π equals approximately 3.1416. In using a calculator, π can be entered to a much greater accuracy by using the π key.

EXAMPLE 2 Area of circle—oil spill

A circular oil spill has a diameter of 2.4 km. It is to be enclosed within special flexible tubing. What is the area of the spill, how long must the tubing be? See Fig. 2.79.

Circular tubing surrounds an oil spill. The spill has a diameter of 2.4 kilometers.

Fig. 2.79

Since d = 2r , r = d / 2 = 1.2 km .  Using Eq. (2.10), the area is

A = πr2 = π(1.2)2 = 4.5 km2

The length of tubing needed is the circumference of the circle. Therefore,

c  = 2πr = 2π(1.2)note that c= πd = 7.5 kmrounded off

Many applied problems involve a combination of geometric figures. The following example illustrates one such combination.

EXAMPLE 3 Perimeter area—machine part

A machine part is a square of side 3.25 in. with a quarter-circle removed (see Fig. 2.80). Find the perimeter the area of the part.

A square with sides of s = 3.25 inches. A quarter circle is shaded with a curve falling from one vertex to the opposite vertex.

Fig. 2.80

Setting up a formula for the perimeter, we add the two sides of length s to one-fourth of the circumference of a circle with radius s. For the area, we subtract the area of one-fourth of a circle from the area of the square. This gives

A diagram illustrates two equations.

where s is the side of the square the radius of the circle. Evaluating, we have

p = 2(3.25) + π(3.25)2 = 11.6 in . A = 3.252 − π(3.25)24 = 2.27 in . 2

CIRCULAR ARCS ANGLES

An arc is part of a circle, an angle formed at the center by two radii is a central angle. The measure of an arc is the same as the central angle between the ends of the radii that define the arc. A sector of a circle is the region bounded by two radii the arc they intercept. A segment of a circle is the region bounded by a chord its arc. (There are two possible segments for a given chord. The smaller region is a minor segment, the larger region is a major segment.) These are illustrated in the following example.

EXAMPLE 4 Sector segment

In Fig. 2.81, a sector of the circle is between radii OA OB arc AB (denoted as AB⌢ ). If the measure of the central angle at O between the radii is 70 ° , the measure of AB⌢  is 70 ° .

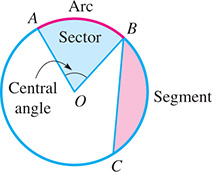
A circle.

Fig. 2.81

A segment of the circle is the region between chord BC arc BC (BC⌢ ).

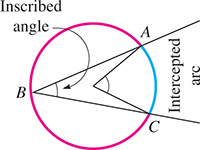
An inscribed angle of an arc is one for which the endpoints of the arc are points on the sides of the angle for which the vertex is a point (not an endpoint) of the arc. An important property of a circle is that the measure of an inscribed angle is one-half of its intercepted arc.

EXAMPLE 5 Inscribed angle

  1. In the circle shown in Fig. 2.82,  ∠ ABC is inscribed in ABC⌢  ,  it intercepts AC⌢  .  If AC⌢  = 60 °  then  ∠ ABC = 30 °  . 

    A circle passes through points Ay, B, and C. A central angle has arc Ay C. Angle Ay B C is an inscribed angle where Ay C is an intercepted arc.

    Fig. 2.82

  2. In the circle shown in Fig. 2.83, PQ is a diameter,  ∠ PRQ is inscribed in the semicircular PRQ⌢  .  Since PSQ⌢  = 180 °  ,   ∠ PRQ = 90 °  .  From this we conclude that an angle inscribed in a semicircle is a right angle.

    Circle O passes through points P, Q, R, and S. Triangle P Q R is inscribed in the semicircular P Q R where P Q is a diameter.

    Fig. 2.83

RADIAN MEASURE OF AN ANGLE

To this point, we have measured all angles in degrees. There is another measure of an angle, the radian, that is defined in terms of an arc of a circle. We will find it of importance when we study trigonometry.

If a central angle of a circle intercepts an arc equal in length to the radius of the circle, the measure of the central angle is defined as 1 radian. See Fig. 2.84. The radius can be marked off along the circumference 2π times (about 6.283 times). Thus, 2π rad = 360 °  (where rad is the symbol for radian), the basic relationship between radians degrees is

π rad = 180 ° 
(2.11)
A circle with radius r and a central angle of 1 radian. The arc length of the central angle equals the radius.

Fig. 2.84

EXAMPLE 6 Radian measure of an angle

  1. If we divide each side of Eq. (2.11) by π ,  we get

    1 rad = 57.3 ° 

    where the result has been rounded off.

  2. To change an angle of 118.2 °  to radian measure, we have

    118.2 °  = 118.2 ° (π rad180 ° ) = 2.06 rad

Multiplying 118.2 °  by π rad  / 180 °  ,  the unit that remains is rad, since degrees “cancel.” We will review radian measure again when we study trigonometry.

EXERCISES 2.4

In Exercises 1–4, answer the given questions about the indicated examples of this section.

  1. In Example 1, if  ∠ AOB = 72 °  in Fig. 2.78, then what is the measure of  ∠ OAB ? 

  2. In the first line of Example 2, if “diameter” is changed to “radius,” what are the results?

  3. In Example 3, if the machine part is the unshaded part (rather than the shaded part) of Fig. 2.80, what are the results?

  4. In Example 5(a), if  ∠ ABC = 25 °  in Fig. 2.82, then what is the measure of AC⌢  ? 

In Exercises 5–8, refer to the circle with center at O in Fig. 2.85. Identify the following.

A circle and an angle.

Fig. 2.85

  1. 5.

    1. A secant line

    2. A tangent line

  2. 6.

    1. Two chords

    2. An inscribed angle

  3. 7.

    1. Two perpendicular lines

    2. An isosceles triangle

  4. 8.

    1. A segment

    2. A sector with an acute central angle

In Exercises 9–12, find the circumference of the circle with the given radius or diameter.

  1. r = 275 ft

  2. r = 0.563 m

  3. d = 23.1 mm

  4. d = 8.2 in . 

In Exercises 13–16, find the area of the circle with the given radius or diameter.

  1. r = 0.0952 yd

  2. r = 45.8 cm

  3. d = 2.33 m

  4. d = 1256 ft

In Exercises 17 and 18, find the area of the circle with the given circumference.

  1. c = 40.1 cm

  2. c = 147 m

In Exercises 19–22, refer to Fig. 2.86, where AB is a diameter, TB is a tangent line at B,  ∠ ABC = 65 °  .  Determine the indicated angles.

Circle O passes through Ay, B, and C with diameter Ay B and inscribed triangle Ay B C. A tangent line passes through B and T, and side Ay C of the triangle extends to point T.

Fig. 2.86

  1.  ∠ CBT

  2.  ∠ BCT

  3.  ∠ CAB

  4.  ∠ BTC

In Exercises 23–26, refer to Fig. 2.87. Determine the indicated arcs angles.

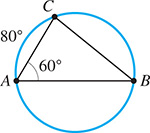
A circle with inscribed triangle Ay B C. Angle Ay is 60 degrees. Arc Ay C is 80 degrees.

Fig. 2.87

  1. BC⌢ 

  2. AB⌢ 

  3.  ∠ ABC

  4.  ∠ ACB

In Exercises 27–30, change the given angles to radian measure.

  1. 22.5 ° 

  2. 60.0 ° 

  3. 125.2 ° 

  4. 323.0 ° 

In Exercises 31–34, find a formula for the indicated perimeter or area.

  1. The perimeter of the quarter-circle in Fig. 2.88.

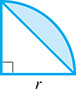
    A quarter circle with radius r. A chord creates a shaded segment and a right triangle where the chord is the hypotenuse.

    Fig. 2.88

  2. The perimeter of the figure in Fig. 2.89. A quarter-circle is attached to a triangle.

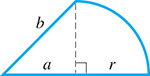
    A quarter circle and a right triangle share a dashed side. The triangle has a leg of ay and hypotenuse of b. The quarter circle has radius r.

    Fig. 2.89

  3. The perimeter of the segment of the quarter-circle in Fig. 2.88.

  4. The area of the figure in Fig. 2.89.

In Exercises 35–58, solve the given problems.

  1. Describe the location of the midpoints of a set of parallel chords of a circle.

  2. The measure of AB⌢  on a circle of radius r is 45 ° . What is the length of the arc in terms of r π ? 

  3. In a circle, a chord connects the ends of two perpendicular radii of 6.00 in. What is the area of the minor segment?

  4. In Fig. 2.90, chords AB DE are parallel. What is the relation between ΔABC ΔCDE ?  Explain.

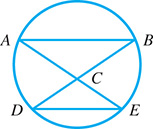
    A circle passes through points Ay, B, E, and D. Point C is within the circle. Triangles Ay B C and C D E share vertex C through sides Ay C E and B C D.

    Fig. 2.90

  5. Equation (2.9) is c = 2πr .  Solve for π ,  then use the equation d = 2r ,  where d is the diameter. State the meaning of the result.

  6. In 1897, the Indiana House of Representatives passed unanimously a bill that included “the … important fact that the ratio of the diameter circumference is as five-fourths to four.” Under this definition, what would be the value of π ?  What is wrong with this House bill statement? (The bill also passed the Senate Committee would have been enacted into law, except for the intervention of a Purdue professor.)

  7. In Fig. 2.91, for the quarter-circle of radius r, find the formula for the segment area A in terms of r.

    A quarter circle of radius r has a dashed chord, h, that creates a segment and a right triangle.

    Fig. 2.91

  8. For the segment in Fig. 2.91, find the segment height h in terms of r.

  9. A person is in a plane 11.5 km above the shore of the Pacific Ocean. How far from the plane can the person see out on the Pacific? (The radius of Earth is 6378 km.)

  10. The CN Tower in Toronto has an observation deck at 346 m above the ground. Assuming ground level Lake Ontario level are equal, how far can a person see from the deck? (The radius of Earth is 6378 km.)

  11. An FM radio station emits a signal that is clear within 85 km of the transmitting tower. Can a clear signal be received at a home 68 km west 58 km south of the tower?

  12. A circular pool 12.0 m in diameter has a sitting ledge 0.60 m wide around it. What is the area of the ledge?

  13. The radius of the Earth’s equator is 3960 mi. What is the circumference?

  14. As a ball bearing rolls along a straight track, it makes 11.0 revolutions while traveling a distance of 109 mm. Find its radius.

  15. The rim on a basketball hoop has an inside diameter of 18.0 in. The largest cross section of a basketball has a diameter of 12.0 in. What is the ratio of the cross-sectional area of the basketball to the area of the hoop?

  16. With no change in the speed of flow, by what factor should the diameter of a fire hose be increased in order to double the amount of water that flows through the fire hose?

  17. Using a tape measure, the circumference of a tree is found to be 112 in. What is the diameter of the tree (assuming a circular cross section)?

  18. Suppose that a 5250-lb force is applied to a hollow steel cylindrical beam that has the cross section shown in Fig. 2.92. The stress on the beam is found by dividing the force by the cross-sectional area. Find the stress.

    A hollow beam has a hollow radius of 2.25 inches and a total radius of 4.00 inches.

    Fig. 2.92

  19. The cross section of a large circular conduit has seven smaller equal circular conduits within it. The conduits are tangent to each other as shown in Fig. 2.93. What fraction of the large conduit is occupied by the seven smaller conduits?

    The cross section of a circular conduit has 7 tangent circular holes within it.

    Fig. 2.93

  20. Find the area of the room in the plan shown in Fig. 2.94.

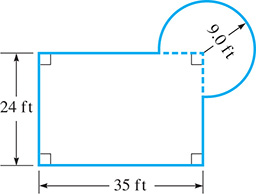
    A diagram of a room.

    Fig. 2.94

  21. Find the length of the pulley belt shown in Fig. 2.95 if the belt crosses at right angles. The radius of each pulley wheel is 5.50 in.

    A pulley diagram with 2 circles. A belt goes over the right circle, rotates under it, then goes over the left circle, rotates under it, and goes back over the right circle. The belt crosses itself at a right angle.

    Fig. 2.95

  22. Two pipes, each with a 25.0-mm-diameter hole, lead into a single larger pipe (see Fig. 2.96). In order to ensure proper flow, the cross-sectional area of the hole of the larger pipe is designed to be equal to the sum of the cross-sectional areas of the two smaller pipes. Find the inside diameter of the larger pipe.

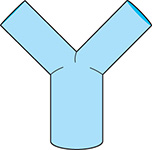
    Three pipes are connected to form a Y-shape. Two smaller pipes feed into a larger pipe.

    Fig. 2.96

  23. The velocity of an object moving in a circular path is directed tangent to the circle in which it is moving. A stone on a string moves in a vertical circle, the string breaks after 5.5 revolutions. If the string was initially in a vertical position, in what direction does the stone move after the string breaks? Explain.

  24. Part of a circular gear with 24 teeth is shown in Fig. 2.97. Find the indicated angle.

    A diagram of a circular gear.

    Fig. 2.97

Answers to Practice Exercises

  1. 126 cm

  2. 1260 cm2

  3. 1.48 rad

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.12.71.146