Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

19.1 Arithmetic Sequences

Arithmetic Sequence • Common Difference• Finite and Infinite Sequences • Sum of n Terms

A sequence of numbers may consist of numbers chosen in any way we may wish to select. This could include a random selection of numbers, although the sequences that are useful follow a pattern. We consider only those sequences that include real numbers or literal numbers that represent real numbers.

An arithmetic sequence (or arithmetic progression) is a set of numbers in which each number after the first can be obtained from the preceding one by adding to it a fixed number called the common difference. This definition can be expressed in terms of the recursion formula

a_{n} = a_{n - 1} + d

$a_{n} = a_{n - 1} + d$ (19.1)

where $a_{n}$ $a_{n}$ is any term, $a_{n - 1}$ $a_{n - 1}$ is the preceding term, and d is the common difference.

EXAMPLE 1 Illustrations of arithmetic sequences

The sequence 2, 5, 8, 11, 14, …, is an arithmetic sequence with a common difference $d = 3.$ $d = 3.$ We can obtain any term by adding 3 to the previous term. We see that the fifth term is $a_{5} = a_{4} + d,$ $a_{5} = a_{4} + d,$ or $14 = 11 + 3.$ $14 = 11 + 3.$
The sequence 7, 2, $- 3, - 8,$ $- 3, - 8,$ …, is an arithmetic sequence with $d = - 5.$ $d = - 5.$ We can get any term after the first by adding $- 5$ $- 5$ to the previous term.

The three dots after the 14 in part (a) and after $- 8$ $- 8$ in part (b) mean that the sequences continue.

If we know the first term of an arithmetic sequence, we can find any other term by adding the common difference enough times to get the desired term. This, however, is very inefficient, and there is a general way of finding a particular term.

If $a_{1}$ $a_{1}$ is the first term and d is the common difference, the second term is $a_{1} + d,$ $a_{1} + d,$ the third term is $a_{1} + 2 d,$ $a_{1} + 2 d,$ and so on. For the nth term, we need to add d to the first term $n - 1$ $n - 1$ times. Therefore, the nth term, $a_{n},$ $a_{n},$ of the arithmetic sequence is given by

a_{n} = a_{1} + (n - 1) d

$a_{n} = a_{1} + (n - 1) d$ (19.2)

Equation (19.2) can be used to find any given term in any arithmetic sequence. We can refer to $a_{n}$ $a_{n}$ as the last term of an arithmetic sequence if no terms beyond it are included in the sequence. Such a sequence is called a finite sequence. If the terms in a sequence continue without end, the sequence is called an infinite sequence.

EXAMPLE 2 Finding a specified term

Find the tenth term of the arithmetic sequence 2, 5, 8, ….

By subtracting any term from the following term, we find the common difference $d = 3,$ $d = 3,$ and see that the first term $a_{1} = 2.$ $a_{1} = 2.$ Therefore, the tenth term, $a_{10},$ $a_{10},$ is

\begin{aligned} a_{10} & = & \overset{\begin{matrix} a_{1} \\ ↓ \end{matrix}}{2} + (\overset{\begin{matrix} n \\ ↓ \end{matrix}}{10} - 1) \overset{\begin{matrix} d \\ ↓ \end{matrix}}{3} = 2 + (9) (3) \\ = & 29 \end{aligned}

$\begin{aligned} a_{10} & = & \overset{\begin{matrix} a_{1} \\ ↓ \end{matrix}}{2} + (\overset{\begin{matrix} n \\ ↓ \end{matrix}}{10} - 1) \overset{\begin{matrix} d \\ ↓ \end{matrix}}{3} = 2 + (9) (3) \\ = & 29 \end{aligned}$

NOTE

[The three dots after the 8 show that the sequence continues. With no additional information given, this indicates that it is an infinite arithmetic sequence.]

EXAMPLE 3 Finding the common difference

Find the common difference between successive terms of the arithmetic sequence for which the third term is 5 and the 34th term is $- 119.$ $- 119.$

In order to use Eq. (19.2), we could calculate $a_{1},$ $a_{1},$ but we can also treat the third term as $a_{1}$ $a_{1}$ and the 34th term as $a_{32} .$ $a_{32} .$ This gives us the same sequence from 5 to $- 119.$ $- 119.$ Therefore, using the values $a_{1} = 5, a_{32} = - 119,$ $a_{1} = 5, a_{32} = - 119,$ and $n = 32,$ $n = 32,$ we can find the value of d. Substituting these values in Eq. (19.2) gives

\begin{matrix} - 119 & = & 5 + (32 - 1) d \\ 31 d & = & - 124 \\ d & = & - 4 \end{matrix}

$\begin{matrix} - 119 & = & 5 + (32 - 1) d \\ 31 d & = & - 124 \\ d & = & - 4 \end{matrix}$

There is no information as to whether this is a finite or an infinite sequence. The solution is the same in either case.

EXAMPLE 4 Finding the number of terms—velocity of a package

A package delivery company uses a metal (very low friction) ramp to slide packages from the sorting area to the loading area below. If a given package is pushed such that it starts down the ramp at 25 cm/s, and the package accelerates as it slides down the ramp such that it gains 35 cm/s during each second, after how many seconds is its velocity 305 cm/s? See Fig. 19.1.

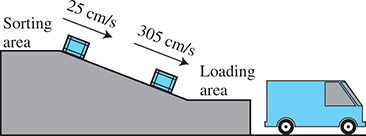
A packing facility where packages begin on a horizontal sorting area. One package is pushed down an incline at 25 centimeters per second, accelerating to 305 centimeters per second to the loading area. — Fig. 19.1

Here, we see that the velocity (in cm/s) of the package after each second is

60, 95, 130, \dots, 305, \dots

$60, 95, 130, \dots, 305, \dots$

Therefore, $a_{1} = 60$ $a_{1} = 60$ (the 25 cm/s was at the beginning, that is, after 0 s), $d = 35, a_{n} = 305,$ $d = 35, a_{n} = 305,$ and we are to find n, which in this case, represents the number of seconds during which the velocity increases. Therefore,

\begin{aligned} 305 & = & 60 + (n - 1) (35) \\ 245 & = & 35 n - 35 \\ 35 n & = & 280 \\ n & = & 8.0 \end{aligned}

$\begin{aligned} 305 & = & 60 + (n - 1) (35) \\ 245 & = & 35 n - 35 \\ 35 n & = & 280 \\ n & = & 8.0 \end{aligned}$

This means that the velocity of a package sliding down the ramp is 305 cm/s after 8.0 s.

SUM OF `n` TERMS

Another important quantity related to an arithmetic sequence is the sum of the first n terms. We can indicate this sum by starting the sum either with the first term or with the last term, as shown by these two equations:

S_{n} = a_{1} + (a_{1} + d) + (a_{1} + 2 d) + \dots + (a_{n} - d) + a_{n}

$S_{n} = a_{1} + (a_{1} + d) + (a_{1} + 2 d) + \dots + (a_{n} - d) + a_{n}$

S_{n} = a_{n} + (a_{n} - d) + (a_{n} - 2 d) + \dots + (a_{1} + d) + a_{1}

$S_{n} = a_{n} + (a_{n} - d) + (a_{n} - 2 d) + \dots + (a_{1} + d) + a_{1}$

If we now add the corresponding members of these two equations, we obtain the result

2 S_{n} = (a_{1} + a_{n}) + (a_{1} + a_{n}) + (a_{1} + a_{n}) + \dots + (a_{1} + a_{n}) + (a_{1} + a_{n})

$2 S_{n} = (a_{1} + a_{n}) + (a_{1} + a_{n}) + (a_{1} + a_{n}) + \dots + (a_{1} + a_{n}) + (a_{1} + a_{n})$

Each term on the right in parentheses has the same expression $(a_{1} + a_{n}),$ $(a_{1} + a_{n}),$ and there are n such terms. This tells us that the sum of the first n terms is given by

S_{n} = \frac{n}{2} (a_{1} + a_{n})

$S_{n} = \frac{n}{2} (a_{1} + a_{n})$ (19.3)

The use of Eq. (19.3) is illustrated in the following examples.

EXAMPLE 5 Finding the sum of terms

Find the sum of the first 1000 positive integers.

The first 1000 positive integers form a finite arithmetic sequence for which $a_{1} = 1, a_{1000} = 1000, n = 1000,$ $a_{1} = 1, a_{1000} = 1000, n = 1000,$ and $d = 1.$ $d = 1.$ Substituting these values in Eq. (19.3) (in which we do not use the value of d), we have

\begin{aligned} S_{1000} & = & \frac{1000}{2} (1 + 1000) = 500 (1001) \\ = & 500, 500 \end{aligned}

$\begin{aligned} S_{1000} & = & \frac{1000}{2} (1 + 1000) = 500 (1001) \\ = & 500, 500 \end{aligned}$

If any three of the five values $a_{1}, a_{n},$ $a_{1}, a_{n},$ n, d, and $S_{n}$ $S_{n}$ are given for a particular arithmetic sequence, the other two may be found from Eqs. (19.2) and (19.3). Consider the following example.

EXAMPLE 6 Finding the sum of terms—increasing voltage

The voltage across a resistor increases such that during each second the increase is 0.002 mV less than during the previous second. Given that the increase during the first second is 0.350 mV, what is the total voltage increase during the first 10.0 s?

We are asked to find the sum of the voltage increases 0.350 mV, 0.348 mV, 0.346 mV, …, so as to include ten increases. This means we want the sum of an arithmetic sequence for which $a_{1} = 0.350, d = - 0.002,$ $a_{1} = 0.350, d = - 0.002,$ and $n = 10.$ $n = 10.$ Because we need $a_{n}$ $a_{n}$ to use Eq. (19.3), we first calculate it, using Eq. (19.2):

a_{10} = 0.350 + (10 - 1) (- 0.002) = 0.332 mV

$a_{10} = 0.350 + (10 - 1) (- 0.002) = 0.332 mV$

Now, we use Eq. (19.3) to find the sum with $a_{1} = 0.350, a_{10} = 0.332,$ $a_{1} = 0.350, a_{10} = 0.332,$ and $n = 10 :$ $n = 10 :$

S_{10} = \frac{10}{2} (0.350 + 0.332) = 3.410 mV

$S_{10} = \frac{10}{2} (0.350 + 0.332) = 3.410 mV$

Thus, the total voltage increase is 3.410 mV.

The summation feature on a calculator can also be used to find the sum of the terms of a sequence. The sums found in Examples 5 and 6 are shown in Fig. 19.2. The symbol $\sum$ $\sum$ (the Greek capital letter sigma) is used to indicate the sum of the terms as the index N ranges between the values shown below and above the $\sum$ $\sum$ symbol.

A calculator screen with input the sum, as N goes from 1 to 1000, of N, and output 500,500; input the sum, as 1 goes to 10, of, 0.35 plus, N minus 1, times, negative 0.002, and output 3.41. — Fig. 19.2
Graphing calculator keystrokes: bit.ly/2A8lOTt

EXERCISES 19.1

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 3, change $- 119$ $- 119$ to $- 88$ $- 88$ and then find the common difference.
In Example 5, change 1000 to 500 and then find the sum.

In Exercises 3–6, write the first five terms of the arithmetic sequence with the given values.

$a_{1} = 4, d = 2$ $a_{1} = 4, d = 2$
$a_{1} = 6, d = - \frac{1}{2}$ $a_{1} = 6, d = - \frac{1}{2}$
$a_{1} = 2.5, a_{5} = - 1.5$ $a_{1} = 2.5, a_{5} = - 1.5$
$a_{2} = - 2, a_{5} = 43$ $a_{2} = - 2, a_{5} = 43$

In Exercises 7–14, find the nth term of the arithmetic sequence with the given values.

1, 4, 7, …; $n = 8$ $n = 8$
$- 6, - 4, - 2, \dots; n = 10$ $- 6, - 4, - 2, \dots; n = 10$
$\frac{8}{3}, \frac{5}{3}, \frac{2}{3}, \dots; n = 9$ $\frac{8}{3}, \frac{5}{3}, \frac{2}{3}, \dots; n = 9$
2, 0.5, $- 1, \dots; n = 25$ $- 1, \dots; n = 25$
$a_{1} = - 0.7, d = 0.4, n = 80$ $a_{1} = - 0.7, d = 0.4, n = 80$
$a_{1} = \frac{3}{2}, d = \frac{1}{6}, n = 601$ $a_{1} = \frac{3}{2}, d = \frac{1}{6}, n = 601$
$a_{1} = b, a_{3} = 5 b, n = 25$ $a_{1} = b, a_{3} = 5 b, n = 25$
$a_{1} = - c, a_{4} = 8 c, n = 30$ $a_{1} = - c, a_{4} = 8 c, n = 30$

In Exercises 15–18, find the sum of the n terms of the indicated arithmetic sequence.

$4 + 8 + 12 + \dots + 64$ $4 + 8 + 12 + \dots + 64$
$27 + 24 + 21 + \dots + (- 9)$ $27 + 24 + 21 + \dots + (- 9)$
$- 2, - \frac{5}{2}, - 3, \dots; n = 10$ $- 2, - \frac{5}{2}, - 3, \dots; n = 10$
$3 k, \frac{10}{3} k, \frac{11}{3} k, \dots; n = 40$ $3 k, \frac{10}{3} k, \frac{11}{3} k, \dots; n = 40$

In Exercises 19–26, find any of the values of $a_{1},$ $a_{1},$ d, $a_{n},$ $a_{n},$ n, or $S_{n}$ $S_{n}$ that are missing for an arithmetic sequence.

5, 13, 21, …, 45
$- 2, - 1.5, - 1, \dots, 28$ $- 2, - 1.5, - 1, \dots, 28$
$a_{1} = \frac{5}{3}, n = 20, S_{20} = \frac{40}{3}$ $a_{1} = \frac{5}{3}, n = 20, S_{20} = \frac{40}{3}$
$d = - 3, n = 3, a_{3} = - 5.9$ $d = - 3, n = 3, a_{3} = - 5.9$
$d = 3, n = 30, S_{30} = 1875$ $d = 3, n = 30, S_{30} = 1875$
$d = 9, n = 18, S_{18} = 1521$ $d = 9, n = 18, S_{18} = 1521$
$a_{1} = 7.4, d = - 0.5, a_{n} = - 23.1$ $a_{1} = 7.4, d = - 0.5, a_{n} = - 23.1$
$a_{1} = - \frac{9}{7}, n = 19, a_{19} = - \frac{36}{7}$ $a_{1} = - \frac{9}{7}, n = 19, a_{19} = - \frac{36}{7}$

In Exercises 27–56, find the indicated quantities for the appropriate arithmetic sequence.

$a_{6} = 560, a_{10} = 720$ $a_{6} = 560, a_{10} = 720$ (find $a_{1},$ $a_{1},$ d, $S_{n}$ $S_{n}$ for $n = 10$ $n = 10$ )
$a_{17} = - 91, a_{2} = - 73$ $a_{17} = - 91, a_{2} = - 73$ (find $a_{1},$ $a_{1},$ d, $S_{n}$ $S_{n}$ for $n = 40$ $n = 40$ )
Is ln 3, ln 6, ln 12, … an arithmetic sequence? Explain. If it is, what is the fifth term?
Is $\sin 2 °, \sin 4 °, \sin 6 °, \dots$ $\sin 2 °, \sin 4 °, \sin 6 °, \dots$ an arithmetic sequence? Explain. If it is, what is the fifth term?
Find a formula with variable n for the nth term of the arithmetic sequence with $a_{1} = 3$ $a_{1} = 3$ and $a_{n + 1} = a_{n} + 2$ $a_{n + 1} = a_{n} + 2$ for $n = 1, 2, 3, \dots.$ $n = 1, 2, 3, \dots.$
In the equation $a_{n} = a_{1} + (n - 1) d,$ $a_{n} = a_{1} + (n - 1) d,$ solve for n.
Write the first five terms of the arithmetic sequence for which the second term is b and the third term is c.
If the sum of the first two terms of an arithmetic sequence equals the sum of the first three terms, find the sum of the first five terms.
Find the sum of the first 100 positive integers. (See the margin note on page 517.)
If x, 5, and $x + 8$ $x + 8$ are the first three terms of an arithmetic sequence, find the sum of the first 20 terms.
Find x if $3 - x, - x,$ $3 - x, - x,$ and $\sqrt{9 - 2 x}$ $\sqrt{9 - 2 x}$ are the first three terms of an arithmetic sequence.
If $x, x + 2 y, 2 x + 3 y, \dots$ $x, x + 2 y, 2 x + 3 y, \dots$ is an arithmetic sequence, express $S_{100}$ $S_{100}$ in terms of x.
The sum of the angles inside a triangle, quadrilateral, and pentagon are $180 °, 360 °,$ $180 °, 360 °,$ and $540 °,$ $540 °,$ respectively. Assuming this pattern continues, what is the sum of the angles inside a dodecagon (12 sides)?
A person begins an exercise program of jogging 10 min each day for the first week. Each week thereafter, the person must increase their daily jogging time by 3 min. During which week will the person be jogging 55 min per day?
A beach now has an area of $9500 m^{2}$ $9500 m^{2}$ but is eroding such that it loses $100 m^{2}$ $100 m^{2}$ more of its area each year than during the previous year. If it lost $400 m^{2}$ $400 m^{2}$ during the last year, what will be its area 8 years from now?
During a period of heavy rains, on a given day $110, {000 ft}^{3} / s$ $110, {000 ft}^{3} / s$ of water was being released from a dam. In order to minimize downstream flooding, engineers then reduced the releases by $10, {000 ft}^{3} / s$ $10, {000 ft}^{3} / s$ each day thereafter. How much water was released during the first week of these releases?
At a logging camp, 15 layers of logs are so piled that there are 20 logs in the bottom layer, and each layer has 1 less log than the layer below it. How many logs are in the pile?
In order to prevent an electric current surge in a circuit, the resistance R in the circuit is stepped down by $4.0 Ω$ $4.0 Ω$ after each 0.1 s. If the voltage V is constant at 120 V, do the resulting currents I (in A) form an arithmetic sequence if $V = I R ?$ $V = I R ?$
There are 12 seats in the first row around a semicircular stage. Each row behind the first has 4 more seats than the row in front of it. How many rows of seats are there if there is a total of 300 seats?
A bank loan of $8000 is repaid in annual payments of $1000 plus 10% interest on the unpaid balance. What is the total amount of interest paid?
A car depreciates $1800 during the first year after it is bought. Each year thereafter it depreciates $150 less than the year before. How many years after it was bought will it be considered to have no value, and what was the original cost?
The sequence of ships’ bells is as follows: 12:30 a.m. one bell is rung, and each half hour later one more bell is rung than the previous time until eight bells are rung. The sequence is then repeated starting at 4:30 a.m., again until eight bells are rung. This pattern is followed throughout the day. How many bells are rung in one day?
When a stone is dropped from the edge of a cliff at the Grand Canyon, it falls 16 ft during the first second, 48 ft during the second second, 80 ft during the third second, 112 ft during the fourth second, and so on. Find (a) the distance the stone falls during the tenth second and (b) the total distance the stone falls during the first 10 seconds.
In preparing a bid for constructing a new building, a contractor determines that the foundation and basement will cost $605,000 and the first floor will cost $360,000. Each floor above the first will cost $15,000 more than the one below it. How much will the building cost if it is to be 18 floors high?
A college graduate is offered two positions. A computer company offers an annual salary of $42,000 with a guaranteed annual raise of $1200. A marketing company offers an annual salary of $44,000 with a guaranteed annual raise of $600. Which company will pay more for the first six years of employment, and how much more?
A person has a $5000 balance due on a credit card account that charges 1% interest per month on the unpaid balance $B_{n} .$ $B_{n} .$ Assuming no extra charges, if $250 is paid each month, find (a) a recursion formula [similar to Eq. (19.1)] for $B_{n}$ $B_{n}$ and (b) $B_{n}$ $B_{n}$ after two months.
Derive a formula for $S_{n}$ $S_{n}$ in terms of n, $a_{1},$ $a_{1},$ and d.
A harmonic sequence is a sequence of numbers whose reciprocals form an arithmetic sequence. Is a harmonic sequence also an arithmetic sequence? Explain.
Show that the sum of the first n positive integers is $\frac{1}{2} n (n + 1) .$ $\frac{1}{2} n (n + 1) .$
Show that the sum of the first n positive odd integers is $n^{2} .$ $n^{2} .$

Answers to Practice Exercises

116
$d = 2.5$ $d = 2.5$
$S_{9} = 81$ $S_{9} = 81$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 19.1 Arithmetic Sequences

Create new playlist

Sign In

Sign Up

Table of Contents for
19.1 Arithmetic Sequences