Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

21.1 Basic Definitions

The Distance Formula • The Slope of a Line • Inclination • Parallel Lines • Perpendicular Lines

As we have noted, analytic geometry deals with the relationship between an algebraic equation and the geometric curve it represents. In this section, we develop certain basic concepts that will be needed for future use in establishing the proper relationships between an equation and a curve.

THE DISTANCE FORMULA

The first of these concepts involves the distance between any two points in the coordinate plane. If these points lie on a line parallel to the x-axis, the distance from the first point $(x_{1}, y)$ $(x_{1}, y)$ to the second point $(x_{2}, y)$ $(x_{2}, y)$ is $| x_{2} - x_{1} | .$ $| x_{2} - x_{1} | .$ The absolute value is used because we are interested only in the magnitude of the distance. Therefore, we could also denote the distance as $| x_{1} - x_{2} | .$ $| x_{1} - x_{2} | .$ Similarly, the distance between two points $(x, y_{1})$ $(x, y_{1})$ and $(x, y_{2})$ $(x, y_{2})$ that lie on a line parallel to the y-axis is $| y_{2} - y_{1} |$ $| y_{2} - y_{1} |$ or $| y_{1} - y_{2} | .$ $| y_{1} - y_{2} | .$

EXAMPLE 1 Distance between points

The line segment joining $A (- 1, 5)$ $A (- 1, 5)$ and $B (- 4, 5)$ $B (- 4, 5)$ in Fig. 21.1 is parallel to the x-axis. Therefore, the distance between these points is

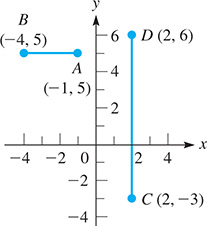
Two line segments. Segment Ay B goes from (negative 1, 5) to (negative 4, 5). Segment C D goes from (2, negative 3) to (2, 6). — Fig. 21.1

d = | - 4 - (- 1) | = 3 or d = | - 1 - (- 4) | = 3

$d = | - 4 - (- 1) | = 3 or d = | - 1 - (- 4) | = 3$

Also, in Fig. 21.1, the line segment joining $C (2, - 3)$ $C (2, - 3)$ and D(2, 6) is parallel to the y-axis. The distance d between these points is

d = | 6 - (- 3) | = 9 or d = | - 3 - 6 | = 9

$d = | 6 - (- 3) | = 9 or d = | - 3 - 6 | = 9$

We now wish to find the length of a line segment joining any two points in the plane. If these points are on a line that is not parallel to either axis (see Fig. 21.2), we use the Pythagorean theorem to find the distance between them. By making a right triangle with the line segment joining the points as the hypotenuse and line segments parallel to the axes as legs, we have $d^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} .$ $d^{2} = {(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} .$ Solving for d, we get the distance formula, which gives the distance between any two points in the plane. This formula is

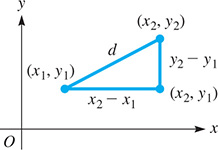
The graph is a right triangle. — Fig. 21.2

Figure 21.2 Full Alternative Text

d = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}

$d = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ (21.1)

Here, we choose the positive square root because we are concerned only with the magnitude of the length of the line segment.

EXAMPLE 2 Distance formula—either point as (`x`₁ , `y`₁)

The distance between $(3, - 1)$ $(3, - 1)$ and $(- 2, - 5)$ $(- 2, - 5)$ is given by

\begin{array}{rcl} d & = & \sqrt{{[(- 2) - 3]}^{2} + {[(- 5) - (- 1)]}^{2}} \\ = & \sqrt{{(- 5)}^{2} + {(- 4)}^{2}} = \sqrt{25 + 16} \\ = & \sqrt{41} = 6.403 \end{array}

$\begin{array}{rcl} d & = & \sqrt{{[(- 2) - 3]}^{2} + {[(- 5) - (- 1)]}^{2}} \\ = & \sqrt{{(- 5)}^{2} + {(- 4)}^{2}} = \sqrt{25 + 16} \\ = & \sqrt{41} = 6.403 \end{array}$

See Fig. 21.3.

A line segment rises from (negative 2, negative 5) to (3, negative 1) with d = 6.403. — Fig. 21.3

NOTE

[It makes no difference which point is chosen as $(x_{1}, y_{1})$ $(x_{1}, y_{1})$ and which is chosen as $(x_{2}, y_{2}),$ $(x_{2}, y_{2}),$ because the differences in the x-coordinates and the y-coordinates are squared.]

We obtain the same value for the distance when we calculate it as

\begin{array}{rcl} d & = & \sqrt{{[3 - (- 2)]}^{2} + {[(- 1) - (- 5)]}^{2}} \\ = & \sqrt{5^{2} + 4^{2}} = \sqrt{41} = 6.403 \end{array}

$\begin{array}{rcl} d & = & \sqrt{{[3 - (- 2)]}^{2} + {[(- 1) - (- 5)]}^{2}} \\ = & \sqrt{5^{2} + 4^{2}} = \sqrt{41} = 6.403 \end{array}$

THE SLOPE OF A LINE

Another important quantity for a line is its slope, which we defined in Chapter 5. Here, we review its definition and develop its meaning in more detail.

The slope of a line through two points is defined as the difference in the y-coordinates (rise) divided by the difference in the x-coordinates (run). Therefore, the slope, m, which gives a measure of the direction of a line, is defined as

m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ (21.2)

See Fig. 21.4.

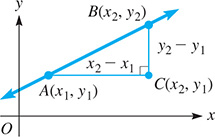
A line rises through Ay (x sub 1, y sub 1) and B (x sub 2, y sub 2). — Fig. 21.4

Figure 21.4 Full Alternative Text

CAUTION

We may interpret either of the points as $(x_{1}, y_{1})$ $(x_{1}, y_{1})$ and the other as $(x_{2}, y_{2}),$ $(x_{2}, y_{2}),$ although we must be careful to place the $y_{2} - y_{1}$ $y_{2} - y_{1}$ in the numerator and $x_{2} - x_{1}$ $x_{2} - x_{1}$ in the denominator.

When the line is horizontal, $y_{2} - y_{1} = 0$ $y_{2} - y_{1} = 0$ and $m = 0.$ $m = 0.$ When the line is vertical, $x_{2} - x_{1} = 0$ $x_{2} - x_{1} = 0$ and the slope is undefined.

EXAMPLE 3 Slope of a line

The slope of a line through $(3, - 5)$ $(3, - 5)$ and $(- 2, - 6)$ $(- 2, - 6)$ is

m = \frac{- 6 - (- 5)}{- 2 - 3} = \frac{- 6 + 5}{- 5} = \frac{1}{5}

$m = \frac{- 6 - (- 5)}{- 2 - 3} = \frac{- 6 + 5}{- 5} = \frac{1}{5}$

See Fig. 21.5. Again, we may interpret either of the points as $(x_{1}, y_{1})$ $(x_{1}, y_{1})$ and the other as $(x_{2}, y_{2}) .$ $(x_{2}, y_{2}) .$ We can also obtain the slope of this same line from

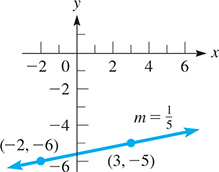
A line rises through (negative 2, negative 6) and (3, negative 5) with slope m = one-fifth. — Fig. 21.5

m = \frac{- 5 - (- 6)}{3 - (- 2)} = \frac{1}{5}

$m = \frac{- 5 - (- 6)}{3 - (- 2)} = \frac{1}{5}$

The larger the numerical value of the slope of a line, the more nearly vertical is the line.

NOTE

[Also, a line rising to the right has a positive slope, and a line falling to the right has a negative slope.]

EXAMPLE 4 Magnitude and sign of slope

The line in Example 3 has a positive slope, which is numerically small. From Fig. 21.5, it can be seen that the line rises slightly to the right.
The line joining (3, 4) and $(4, - 6)$ $(4, - 6)$ has a slope of

$m = \frac{4 - (- 6)}{3 - 4} = - 10 or m = \frac{- 6 - 4}{4 - 3} = - 10$ $m = \frac{4 - (- 6)}{3 - 4} = - 10 or m = \frac{- 6 - 4}{4 - 3} = - 10$

This line falls sharply to the right, as shown in Fig. 21.6.

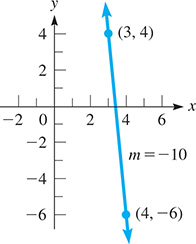
A line falls through (3, 4) and (4, negative 6) with slope m = negative 10. — Fig. 21.6

If a given line is extended indefinitely in either direction, it must cross the x-axis at some point unless it is parallel to the x-axis. The angle measured from the x-axis in a positive direction to the line is called the inclination of the line (see Fig. 21.7). The inclination of a line parallel to the x-axis is defined to be zero. An alternate definition of slope, in terms of the inclination $α,$ $α,$ is

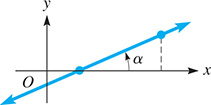
A line rises through the positive x-axis and a point in quadrant 1. The counterclockwise angle from the positive x-axis to the line is alpha. — Fig. 21.7

m = \tan α (0 ° \leq α < 180 °)

$m = \tan α (0 ° \leq α < 180 °)$ (21.3)

Because the slope can be defined in terms of any two points on the line, we can choose the x-intercept and any other point. Therefore, from the definition of the tangent of an angle, we see that Eq. (21.3) is in agreement with Eq. (21.2).

EXAMPLE 5 Inclination

The slope of a line with an inclination of $45 °$ $45 °$ is

$m = \tan 45 ° = 1.000$ $m = \tan 45 ° = 1.000$
If a line has a slope of $- 1.732,$ $- 1.732,$ we know that $\tan α = - 1.732.$ $\tan α = - 1.732.$ Because $\tan α$ $\tan α$ is negative, $α$ $α$ must be a second-quadrant angle. Therefore, using a calculator to show that $\tan 60 ° = 1.732,$ $\tan 60 ° = 1.732,$ we find that $α = 180 ° - 60 ° = 120 ° .$ $α = 180 ° - 60 ° = 120 ° .$ See Fig. 21.8.

Figure 21.8 Full Alternative Text

We see that if the inclination is an acute angle, the slope is positive and the line rises to the right. If the inclination is an obtuse angle, the slope is negative and the line falls to the right.

Any two parallel lines crossing the x-axis have the same inclination. Therefore, as shown in Fig. 21.9, the slopes of parallel lines are equal. This can be stated as

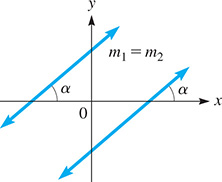
Two lines rises with parallel slopes, m sub 1 = m sub 2. One line has inclination alpha with the positive x-axis, and the other has inclination alpha with the negative x-axis. — Fig. 21.9

\begin{array}{l} m_{1} = m_{2} & (for | | lines) \end{array}

$\begin{array}{l} m_{1} = m_{2} & (for | | lines) \end{array}$ (21.4)

If two lines are perpendicular, this means that there must be $90 °$ $90 °$ between their inclinations (Fig. 21.10). The relation between their inclinations is

Two perpendicular lines that meet on the positive y-axis. One line rises with acute inclination alpha sub 1, and the other falls with obtuse inclination alpha sub 2. — Fig. 21.10

\begin{array}{rcl} α_{2} & = & α_{1} + 90 ° \\ 90 ° - α_{2} & = & - α_{1} \end{array}

$\begin{array}{rcl} α_{2} & = & α_{1} + 90 ° \\ 90 ° - α_{2} & = & - α_{1} \end{array}$

If neither line is vertical (the slope of a vertical line is undefined) and we take the tangent in this last relation, we have

\tan (90 ° - α_{2}) = \tan (- α_{1})

$\tan (90 ° - α_{2}) = \tan (- α_{1})$

\cot α_{2} = - \tan α_{1}

$\cot α_{2} = - \tan α_{1}$

because a function of the complement of an angle equals the cofunction of that angle (see page 125) and because $\tan (- α) = - \tan α$ $\tan (- α) = - \tan α$ (see page 247). But $\cot α = 1 / \tan α,$ $\cot α = 1 / \tan α,$ which means $1 / \tan α_{2} = - \tan α_{1} .$ $1 / \tan α_{2} = - \tan α_{1} .$ Using the inclination definition of slope, we have as the relation between slopes of perpendicular lines,

\begin{array}{l} \begin{array}{l} m_{2} = - \frac{1}{m_{1}} & or & m_{1} m_{2} = - 1 \end{array} & for ⊥ lines \end{array}

$\begin{array}{l} \begin{array}{l} m_{2} = - \frac{1}{m_{1}} & or & m_{1} m_{2} = - 1 \end{array} & for ⊥ lines \end{array}$ (21.5)

EXAMPLE 6 Perpendicular lines

The line through $(3, - 5)$ $(3, - 5)$ and $(2, - 7)$ $(2, - 7)$ has a slope of

m_{1} = \frac{- 5 + 7}{3 - 2} = 2

$m_{1} = \frac{- 5 + 7}{3 - 2} = 2$

The line through $(4, - 6)$ $(4, - 6)$ and $(2, - 5)$ $(2, - 5)$ has a slope of

m_{2} = \frac{- 6 - (- 5)}{4 - 2} = - \frac{1}{2}

$m_{2} = \frac{- 6 - (- 5)}{4 - 2} = - \frac{1}{2}$

Because the slopes of the two lines are negative reciprocals, we know that the lines are perpendicular. See Fig. 21.11.

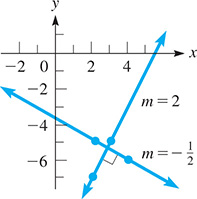
Two perpendicular lines. One line rises through (2, negative 7) and (3, negative 5) with slope m = 2, and the other falls through (2, negative 5) and (4, negative 6) with slope m = negative one-half. — Fig. 21.11

Using the formulas for distance and slope, we can show certain basic geometric relationships. The following examples illustrate the use of the formulas and thereby show the use of algebra in solving problems that are basically geometric. This illustrates the methods of analytic geometry.

EXAMPLE 7 Use of algebra in geometric problems

Show that the line segments joining $A (- 5, 3),$ $A (- 5, 3),$ B(6, 0), and C(5, 5) form a right triangle. See Fig. 21.12.

Fig. 21.12

If these points are vertices of a right triangle, the slopes of two of the sides must be negative reciprocals. This would show perpendicularity. These slopes are

$m_{A B} = \frac{3 - 0}{- 5 - 6} = - \frac{3}{11} m_{A C} = \frac{3 - 5}{- 5 - 5} = \frac{1}{5} m_{B C} = \frac{0 - 5}{6 - 5} = - 5$ $m_{A B} = \frac{3 - 0}{- 5 - 6} = - \frac{3}{11} m_{A C} = \frac{3 - 5}{- 5 - 5} = \frac{1}{5} m_{B C} = \frac{0 - 5}{6 - 5} = - 5$

We see that the slopes of AC and BC are negative reciprocals, which means $A C ⊥ B C .$ $A C ⊥ B C .$ From this we conclude that the triangle is a right triangle.
Find the area of the triangle in part (a). See Fig. 21.13.

Fig. 21.13

Because the right angle is at C, the legs of the triangle are AC and BC. The area is one-half the product of the lengths of the legs of a right triangle. The lengths of the legs are

$\begin{array}{rcl} d_{A C} & = & \sqrt{{(- 5 - 5)}^{2} + {(3 - 5)}^{2}} = \sqrt{104} = 2 \sqrt{26} \\ d_{B C} & = & \sqrt{{(6 - 5)}^{2} + {(0 - 5)}^{2}} = \sqrt{26} \end{array}$ $\begin{array}{rcl} d_{A C} & = & \sqrt{{(- 5 - 5)}^{2} + {(3 - 5)}^{2}} = \sqrt{104} = 2 \sqrt{26} \\ d_{B C} & = & \sqrt{{(6 - 5)}^{2} + {(0 - 5)}^{2}} = \sqrt{26} \end{array}$

Therefore, the area is $A = \frac{1}{2} (2 \sqrt{26}) (\sqrt{26}) = 26.$ $A = \frac{1}{2} (2 \sqrt{26}) (\sqrt{26}) = 26.$

Exercises 21.1

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 2, change $(- 2, - 5)$ $(- 2, - 5)$ to $(- 2, 5) .$ $(- 2, 5) .$
In Example 3, change $(3, - 5)$ $(3, - 5)$ to $(- 3, - 5) .$ $(- 3, - 5) .$
In Example 5(b), change $- 1.732$ $- 1.732$ to $- 0.5774.$ $- 0.5774.$
In Example 7(a), change B(6, 0) to $B (- 4, - 2) .$ $B (- 4, - 2) .$

In Exercises 5–14, find the distance between the given pairs of points.

(3, 8) and $(- 1, - 2)$ $(- 1, - 2)$
$(- 1, 3)$ $(- 1, 3)$ and $(- 8, - 4)$ $(- 8, - 4)$
$(4, - 5)$ $(4, - 5)$ and $(4, - 8)$ $(4, - 8)$
$(- 3, - 7)$ $(- 3, - 7)$ and (2, 10)
$(- 12, 20)$ $(- 12, 20)$ and $(32, - 13)$ $(32, - 13)$
$(23, - 9)$ $(23, - 9)$ and $(- 25, 11)$ $(- 25, 11)$
$(\sqrt{32}, \sqrt{18})$ $(\sqrt{32}, \sqrt{18})$ and $(- \sqrt{50}, \sqrt{8})$ $(- \sqrt{50}, \sqrt{8})$
$(e, - π)$ $(e, - π)$ and $(- 2 e, - π)$ $(- 2 e, - π)$
$(1.22, - 3.45)$ $(1.22, - 3.45)$ and $(- 1.07, - 5.16)$ $(- 1.07, - 5.16)$
$(a, h^{2})$ $(a, h^{2})$ and $[a + h, {(a + h)}^{2}]$ $[a + h, {(a + h)}^{2}]$

In Exercises 15–24, find the slopes of the lines through the points in Exercises 5–14.

In Exercises 25–28, find the slopes of the lines with the given inclinations.

$30 °$ $30 °$
$62.5 °$ $62.5 °$
$176.2 °$ $176.2 °$
$93.5 °$ $93.5 °$

In Exercises 29–32, find the inclinations of the lines with the given slopes.

0.364
1.903
$- 6.691$ $- 6.691$
$- 0.0721$ $- 0.0721$

In Exercises 33–36, determine whether the lines through the two pairs of points are parallel or perpendicular.

$(6, - 1)$ $(6, - 1)$ and (4, 3); $(- 5, 2)$ $(- 5, 2)$ and $(- 7, 6)$ $(- 7, 6)$
$(- 3, 9)$ $(- 3, 9)$ and (4, 4); $(9, - 1)$ $(9, - 1)$ and $(4, - 8)$ $(4, - 8)$
$(- 1, - 4)$ $(- 1, - 4)$ and (2, 3); $(- 5, 2)$ $(- 5, 2)$ and $(- 19, 8)$ $(- 19, 8)$
$(- a, - 2 b)$ $(- a, - 2 b)$ and (3a, 6b); $(2 a, - 6 b)$ $(2 a, - 6 b)$ and (5a, 0)

In Exercises 37–40, determine the value of k.

The distance between $(- 1, 3)$ $(- 1, 3)$ and (11, k) is 13.
The distance between (k, 0) and (0, 2k) is 10.
Points $(6, - 1), (3, k),$ $(6, - 1), (3, k),$ and $(- 3, - 7)$ $(- 3, - 7)$ are on the same line.
The points in Exercise 39 are the vertices of a right triangle, with the right angle at (3, k).

In Exercises 41–44, show that the given points are vertices of the given geometric figures.

(2, 3), (4, 9), and $(- 2, 7)$ $(- 2, 7)$ are vertices of an isosceles triangle.
$(- 1, 3),$ $(- 1, 3),$ (3, 5), and (5, 1) are the vertices of a right triangle.
$(- 5, - 4),$ $(- 5, - 4),$ (7, 1), (10, 5), and $(- 2, 0)$ $(- 2, 0)$ are the vertices of a parallelogram.
$(- 5, 6),$ $(- 5, 6),$ (0, 8), $(- 3, 1),$ $(- 3, 1),$ and (2, 3) are the vertices of a square.

In Exercises 45–48, find the indicated areas and perimeters.

Find the area of the triangle in Exercise 42.
Find the area of the square in Exercise 44.
Find the perimeter of the triangle in Exercise 41.
Find the perimeter of the parallelogram in Exercise 43.

In Exercises 49–52, use the following definition to find the midpoints between the given points on a straight line.

The midpoint between points $(x_{1}, y_{1})$ $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ $(x_{2}, y_{2})$ on a straight line is the point.

(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})

$(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

$(- 4, 9)$ $(- 4, 9)$ and (6, 1)
$(- 1, 6)$ $(- 1, 6)$ and $(- 13, - 8)$ $(- 13, - 8)$
$(- 12.4, 25.7)$ $(- 12.4, 25.7)$ and $(6.8, - 17.3)$ $(6.8, - 17.3)$
(2.6, 5.3) and $(- 4.2, - 2.7)$ $(- 4.2, - 2.7)$

In Exercises 53–66, solve the given problems.

Find the relation between x and y such that (x, y) is always 3 units from the origin.
Find the relation between x and y such that (x, y) is always equidistant from the y-axis and (2, 0).
Show that the diagonals of a square are perpendicular to each other. [Hint: Use (0, 0), (a, 0), and (0, a) as three of the vertices.]
The center of a circle is $(2, - 3),$ $(2, - 3),$ and one end of a diameter is $(- 1, 2) .$ $(- 1, 2) .$ What are the coordinates of the other end of the diameter?
A line segment has a slope of 3 and one endpoint at $(- 2, 5) .$ $(- 2, 5) .$ If the other endpoint is on the x-axis, what are its coordinates?
The points $(- 1, 3),$ $(- 1, 3),$ (5, y), and (2, 4) are collinear (on the same line). Find y.
Find the coordinates of the point on the y-axis that is equidistant from $(- 3, - 5)$ $(- 3, - 5)$ and (2, 4).
Are the points (3, 5), $(1, - 1),$ $(1, - 1),$ and (6, 14) collinear?
Are the points $(- 1, 6)$ $(- 1, 6)$ and (5, 5) equidistant from (2, 1)?
The grade of a highway is its slope expressed as a percent (a 5% grade means the slope is $\frac{5}{100}$ $\frac{5}{100}$ ). If the grade of a certain highway is 6%, find (a) its angle of inclination and (b) the change in elevation (in ft) of a car driving for 2.00 mi uphill along this highway $(1 mi = 5280 ft) .$ $(1 mi = 5280 ft) .$
On a computer drawing showing the specifications for a mounting bracket, holes are to be drilled at the points (32.5, 25.5) and (88.0, 62.5), where all measurements are in mm. Find the distance between the centers of the two holes.
A triangular machine part has vertices at $A (- 3, 6), B (- 1, 1)$ $A (- 3, 6), B (- 1, 1)$ , and C(5, 2). What is the length of the median from $(- 1, 1) ?$ $(- 1, 1) ?$ See Fig. 21.14. (A median is a line segment that connects a vertex with the midpoint of the opposite side. See Exercises 49–52.)

Fig. 21.14
Denver is 1350 km east and 900 km south of Seattle. Edmonton is 620 km east and 640 km north of Seattle. How far is Denver from Edmonton?
A person is working out on a treadmill inclined at 12% (the slope of the treadmill expressed in percent). What is the angle between the treadmill and the horizontal?

Answers to Practice Exercises

$d = \sqrt{130} = 11.4$ $d = \sqrt{130} = 11.4$
$m = - 2/9$ $m = - 2/9$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 21.1 Basic Definitions

Create new playlist

Sign In

Sign Up

Table of Contents for
21.1 Basic Definitions