Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

20.5 Solving Trigonometric Equations

Solve for Trig Function - Then Angle • Use Algebraic Methods and Trigonometric Identities • Use of Calculator

One of the most important uses of the trigonometric identities is in the solution of equations involving trigonometric functions. The solution of this type of equation consists of the angles that satisfy the equation. When solving for the angle, we generally first solve for a value of a function of the angle and then find the angle from this value of the function.

When equations are written in terms of more than one function, the identities provide a way of changing many of them to equations or factors involving only one function of the same angle. Thus, the solution is found by using algebraic methods and trigonometric identities and values. From Chapter 8, recall that we must be careful regarding the sign of the value of a trigonometric function in finding the angle. Figure 20.26 shows again the quadrants in which the functions are positive. Functions not listed are negative.

A coordinate system with positive functions. — Fig. 20.26

Figure 20.26 Full Alternative Text

EXAMPLE 1 First solve for cos `θ`

Solve the equation $2 \cos θ - 1 = 0$ $2 \cos θ - 1 = 0$ for all values of $θ$ $θ$ such that $0 \leq θ \leq 2 π .$ $0 \leq θ \leq 2 π .$

Solving the equation for $\cos θ,$ $\cos θ,$ we obtain $\cos θ = \frac{1}{2} .$ $\cos θ = \frac{1}{2} .$ The problem asks for all values of $θ$ $θ$ from 0 to $2 π$ $2 π$ that satisfy the equation. We know that the cosines of angles in the first and fourth quadrants are positive. Also, we know that $\cos \frac{π}{3} = \frac{1}{2},$ $\cos \frac{π}{3} = \frac{1}{2},$ which means that $\frac{π}{3}$ $\frac{π}{3}$ is the reference angle. Therefore, the solution proceeds as follows:

\begin{array}{rcll} 2 \cos θ - 1 & = & 0 \\ 2 \cos θ & = & 1 & solve for \cos θ \\ \cos θ & = & \frac{1}{2} \\ θ & = & \frac{π}{3}, \frac{5 π}{3} & θ in quadrants I and IV \end{array}

$\begin{array}{rcll} 2 \cos θ - 1 & = & 0 \\ 2 \cos θ & = & 1 & solve for \cos θ \\ \cos θ & = & \frac{1}{2} \\ θ & = & \frac{π}{3}, \frac{5 π}{3} & θ in quadrants I and IV \end{array}$

EXAMPLE 2 Use identity—factor—solve for sin `x`

Solve the equation $2 \cos^{2} x - \sin x - 1 = 0 (0 \leq x < 2 π) .$ $2 \cos^{2} x - \sin x - 1 = 0 (0 \leq x < 2 π) .$

By use of the identity $\sin^{2} x + \cos^{2} x = 1,$ $\sin^{2} x + \cos^{2} x = 1,$ this equation may be put in terms of sin x only. Thus, we have

\begin{array}{rcll} 2 (1 - \sin^{2} x) - \sin x - 1 & = & 0 & use identity \\ - 2 \sin^{2} x - \sin x + 1 & = & 0 & solve for \sin x \\ 2 \sin^{2} x + \sin x - 1 & = & 0 \\ (2 \sin x - 1) (\sin x + 1) & = & 0 & factor \end{array}

$\begin{array}{rcll} 2 (1 - \sin^{2} x) - \sin x - 1 & = & 0 & use identity \\ - 2 \sin^{2} x - \sin x + 1 & = & 0 & solve for \sin x \\ 2 \sin^{2} x + \sin x - 1 & = & 0 \\ (2 \sin x - 1) (\sin x + 1) & = & 0 & factor \end{array}$

Setting each factor equal to zero, we find $\sin x = 1/2,$ $\sin x = 1/2,$ or $\sin x = - 1 .$ $\sin x = - 1 .$ For the domain 0 to $2 π, \sin x = 1/2$ $2 π, \sin x = 1/2$ gives $x = π / 6, 5 π / 6,$ $x = π / 6, 5 π / 6,$ and $\sin x = - 1$ $\sin x = - 1$ gives $x = 3 π / 2 .$ $x = 3 π / 2 .$ Therefore,

x = \frac{π}{6}, \frac{5 π}{6}, \frac{3 π}{2}

$x = \frac{π}{6}, \frac{5 π}{6}, \frac{3 π}{2}$

These values check when substituted in the original equation.

GRAPHICAL SOLUTIONS

As with algebraic equations, graphical solutions of trigonometric equations are approximate, whereas algebraic solutions often give exact solutions. As before, we collect all terms on the left of the equal sign, with zero on the right. We then graph the function on the left to find its zeros by finding the values of x where the graph crosses (or is tangent to) the x-axis.

EXAMPLE 3 Solution using calculator

Graphically solve the equation $2 \cos^{2} x - \sin x - 1 = 0 (0 \leq x < 2 π)$ $2 \cos^{2} x - \sin x - 1 = 0 (0 \leq x < 2 π)$ by using a calculator. (This is the same equation as in Example 2.)

Because all the terms of the equation are on the left, with zero on the right, we now set $y = 2 \cos^{2} x - \sin x - 1 .$ $y = 2 \cos^{2} x - \sin x - 1 .$ We then enter this function in the calculator as $Y_{1},$ $Y_{1},$ and the graph is displayed in Fig. 20.27. Using the zero feature of a calculator, we find that $y = 0$ $y = 0$ for

A curve begins at (0, 1), falls to (pi over 2, negative 2), rises to (pi, 1), falls to (3 pi over 2, 0), then rises to (2 pi, 1). All data are approximate. — Fig. 20.27

x = 0.52, 2.62, 4.71

$x = 0.52, 2.62, 4.71$

These values are the same as in Example 2. We note that for $x = 4.71,$ $x = 4.71,$ the curve touches the x-axis but does not cross it. This means it is tangent to the x-axis.

EXAMPLE 4 Solve—check for extraneous solutions

Solve the equation $\cos (x / 2) = 1 + \cos x (0 \leq x < 2 π) .$ $\cos (x / 2) = 1 + \cos x (0 \leq x < 2 π) .$

By using the half-angle formula for cos (x/2) and then squaring both sides of the resulting equation, this equation can be solved:

\begin{array}{rcll} \pm \sqrt{\frac{1 + \cos x}{2}} & = & 1 + \cos x & using identity \\ \frac{1 + \cos x}{2} & = & 1 + 2 \cos x + \cos^{2} x & squaring both sides \\ 2 \cos^{2} x + 3 \cos x + 1 & = & 0 & simplifying \\ (2 \cos x + 1) (\cos x + 1) & = & 0 & factoring \\ \cos x & = & - \frac{1}{2}, - 1 \\ x & = & \frac{2 π}{3}, \frac{4 π}{3}, π \end{array}

$\begin{array}{rcll} \pm \sqrt{\frac{1 + \cos x}{2}} & = & 1 + \cos x & using identity \\ \frac{1 + \cos x}{2} & = & 1 + 2 \cos x + \cos^{2} x & squaring both sides \\ 2 \cos^{2} x + 3 \cos x + 1 & = & 0 & simplifying \\ (2 \cos x + 1) (\cos x + 1) & = & 0 & factoring \\ \cos x & = & - \frac{1}{2}, - 1 \\ x & = & \frac{2 π}{3}, \frac{4 π}{3}, π \end{array}$

CAUTION

In finding this solution, we squared both sides of the original equation. In doing this, we may have introduced extraneous solutions (see Section 14.3). Thus, we must check each solution in the original equation to see if it is valid.

Hence,

\begin{array}{lrclcrclcr} x = \frac{2 π}{3} : & \cos \frac{π}{3} & \overset{?}{=} & 1 + \cos \frac{2 π}{3} & or & \frac{1}{2} & \overset{?}{=} & 1 + (- \frac{1}{2}) & or & \frac{1}{2} = \frac{1}{2} \\ x = \frac{4 π}{3} : & \cos \frac{2 π}{3} & \overset{?}{=} & 1 + \cos \frac{4 π}{3} & or & - \frac{1}{2} & \overset{?}{=} & 1 + (- \frac{1}{2}) & or & - \frac{1}{2} \neq \frac{1}{2} \\ x = π : & \cos \frac{π}{2} & \overset{?}{=} & 1 + \cos π & or & 0 & \overset{?}{=} & 1 - 1 & or & 0 = 0 \end{array}

$\begin{array}{lrclcrclcr} x = \frac{2 π}{3} : & \cos \frac{π}{3} & \overset{?}{=} & 1 + \cos \frac{2 π}{3} & or & \frac{1}{2} & \overset{?}{=} & 1 + (- \frac{1}{2}) & or & \frac{1}{2} = \frac{1}{2} \\ x = \frac{4 π}{3} : & \cos \frac{2 π}{3} & \overset{?}{=} & 1 + \cos \frac{4 π}{3} & or & - \frac{1}{2} & \overset{?}{=} & 1 + (- \frac{1}{2}) & or & - \frac{1}{2} \neq \frac{1}{2} \\ x = π : & \cos \frac{π}{2} & \overset{?}{=} & 1 + \cos π & or & 0 & \overset{?}{=} & 1 - 1 & or & 0 = 0 \end{array}$

Thus, the apparent solution $x = \frac{4 π}{3}$ $x = \frac{4 π}{3}$ is not a solution of the original equation. The correct solutions are $x = \frac{2 π}{3}$ $x = \frac{2 π}{3}$ and $x = π .$ $x = π .$ We can see that these values agree with the values of x for which the graph of $y_{1} = \cos (x / 2) - 1 - \cos x$ $y_{1} = \cos (x / 2) - 1 - \cos x$ crosses the x-axis in Fig. 20.28.

A curve begins at (0, negative 1), rises through (2 pi over 3, 0) into quadrant 1, then falls through (pi, 0). — Fig. 20.28

EXAMPLE 5 Trig equation—spring displacement

The vertical displacement y of an object at the end of a spring, which itself is being moved up and down, is given by $y = 3.50 \sin t + 1.20 \sin 2 t .$ $y = 3.50 \sin t + 1.20 \sin 2 t .$ Find the first two values of t (in seconds) for which $y = 0 .$ $y = 0 .$

Using the double-angle formula for sin 2t leads to the solution.

\begin{array}{rcll} 3.50 \sin t + 1.20 \sin 2 t & = & 0 & setting y = 0 \\ 3.50 \sin t + 2.40 \sin t \cos t & = & 0 & using identities \\ \sin t (3.50 + 2.40 \cos t) & = & 0 & factoring \\ \sin t & = & 0 & or \cos t = - 1.46 \\ t & = & 0.00, & 3.14, \dots \end{array}

$\begin{array}{rcll} 3.50 \sin t + 1.20 \sin 2 t & = & 0 & setting y = 0 \\ 3.50 \sin t + 2.40 \sin t \cos t & = & 0 & using identities \\ \sin t (3.50 + 2.40 \cos t) & = & 0 & factoring \\ \sin t & = & 0 & or \cos t = - 1.46 \\ t & = & 0.00, & 3.14, \dots \end{array}$

Because cos t cannot be numerically larger than 1, there are no values of t for which $\cos t = - 1.46 .$ $\cos t = - 1.46 .$ Thus, the required times are $t = 0.00 s, 3.14 s .$ $t = 0.00 s, 3.14 s .$

We can see that these values agree with the values of t for which the graph of $y = 3.50 \sin t + 1.20 \sin 2 t$ $y = 3.50 \sin t + 1.20 \sin 2 t$ crosses the t-axis in Fig. 20.29. (In using a graphing calculator, use x for t.)

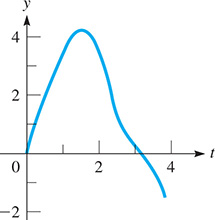
A curve begins at (0, 0), rises to (1.4, 4.2), falls and inflects at (2.4, 1), then falls through (3.14, 0) to (4, negative 1.2). All data are approximate. — Fig. 20.29

EXAMPLE 6 Solve for 2`θ`—then `θ`

Solve the equation $\tan 2 θ - \cot 2 θ = 0 (0 \leq θ < 2 π) .$ $\tan 2 θ - \cot 2 θ = 0 (0 \leq θ < 2 π) .$

\begin{array}{rcll} \tan 2 θ - \frac{1}{\tan 2 θ} & = & 0 & using \cot 2 θ = \frac{1}{\tan 2 θ} \\ \tan^{2} 2 θ & = & 1 & multiplying by \tan 2 θ and adding 1 to each side \\ \tan 2 θ & = & \pm 1 & taking square roots \end{array}

$\begin{array}{rcll} \tan 2 θ - \frac{1}{\tan 2 θ} & = & 0 & using \cot 2 θ = \frac{1}{\tan 2 θ} \\ \tan^{2} 2 θ & = & 1 & multiplying by \tan 2 θ and adding 1 to each side \\ \tan 2 θ & = & \pm 1 & taking square roots \end{array}$

For $0 \leq θ < 2 π,$ $0 \leq θ < 2 π,$ we must have values of $2 θ$ $2 θ$ such that $0 \leq 2 θ < 4 π .$ $0 \leq 2 θ < 4 π .$ Therefore,

2 θ = \frac{π}{4}, \frac{3 π}{4}, \frac{5 π}{4}, \frac{7 π}{4}, \frac{9 π}{4}, \frac{11 π}{4}, \frac{13 π}{4}, \frac{15 π}{4}

$2 θ = \frac{π}{4}, \frac{3 π}{4}, \frac{5 π}{4}, \frac{7 π}{4}, \frac{9 π}{4}, \frac{11 π}{4}, \frac{13 π}{4}, \frac{15 π}{4}$

This means that the solutions are

θ = \frac{π}{8}, \frac{3 π}{8}, \frac{5 π}{8}, \frac{7 π}{8}, \frac{9 π}{8}, \frac{11 π}{8}, \frac{13 π}{8}, \frac{15 π}{8}

$θ = \frac{π}{8}, \frac{3 π}{8}, \frac{5 π}{8}, \frac{7 π}{8}, \frac{9 π}{8}, \frac{11 π}{8}, \frac{13 π}{8}, \frac{15 π}{8}$

These values satisfy the original equation. Because we multiplied through by $\tan 2 θ$ $\tan 2 θ$ in the solution, any value of $θ$ $θ$ that leads to $\tan 2 θ = 0$ $\tan 2 θ = 0$ would not be valid, because this would indicate division by zero in the original equation.

We see that these solutions agree with the values of $θ$ $θ$ for which the graph of $y = \cos 2 θ - \cot 2 θ$ $y = \cos 2 θ - \cot 2 θ$ crosses the $θ - axis$ $θ - axis$ in Fig. 20.30. (In using a graphing calculator, use x for $θ .$ $θ .$

The graph is periodic about the horizontal axis. Each cycle rises with decreasing steepness, inflects on the horizontal axis, then rises with increasing steepness. — Fig. 20.30

EXAMPLE 7 Recognize trigonometric form—solve

Solve the equation $\cos 3 x \cos x + \sin 3 x \sin x = 1 (0 \leq x < 2 π) .$ $\cos 3 x \cos x + \sin 3 x \sin x = 1 (0 \leq x < 2 π) .$

The left side of this equation is of the general form $\cos (A - x),$ $\cos (A - x),$ where $A = 3 x .$ $A = 3 x .$ Therefore,

\cos 3 x \cos x + \sin 3 x \sin x = \cos (3 x - x) = \cos 2 x

$\cos 3 x \cos x + \sin 3 x \sin x = \cos (3 x - x) = \cos 2 x$

The original equation becomes

\cos 2 x = 1

$\cos 2 x = 1$

This equation is satisfied if $2 x = 0$ $2 x = 0$ or $2 x = 2 π .$ $2 x = 2 π .$ The solutions are $x = 0$ $x = 0$ and $x = π .$ $x = π .$ Only through recognition of the proper trigonometric form can we readily solve this equation.

We see that these solutions agree with the two values of x for which the graph of $y = \cos 3 x \cos x + \sin 3 x \sin x - 1$ $y = \cos 3 x \cos x + \sin 3 x \sin x - 1$ touches the x-axis in Fig. 20.31.

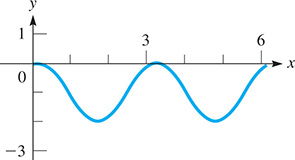
A curve oscillates about y = negative 1 with amplitude 1, period pi, and maximum (pi, 0). All data are approximate. — Fig. 20.31

EXAMPLE 8 Solve using calculator—height of tsunami wave

Aerial photographs and computer analysis show that a certain tsunami wave could be represented as $y = 4 \sin 0.2 x + \frac{60}{0.005 x^{2} + 2},$ $y = 4 \sin 0.2 x + \frac{60}{0.005 x^{2} + 2},$ where y (in m) is the height of the wave for a horizontal displacement x (in m). Find the height of the peak of the wave and the displacement x for the peak.

Entering the function in the calculator as $y_{1},$ $y_{1},$ the graph is shown in Fig. 20.32. We can find the coordinates of the peak of the wave using the maximum feature, as shown in the display. Thus, the peak of the wave is 31.7 m when $x = 4.0 m .$ $x = 4.0 m .$

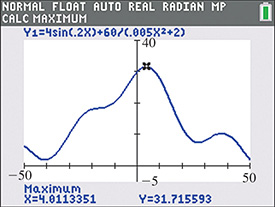
The curve y sub 1 = 4 times sine of, 0.2 x, plus 60 divided by, 0.005 x squared plus 2, rises to maximum (4.0113351, 31.715593). — Fig. 20.32

EXERCISES 20.5

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 1, change $2 \cos θ$ $2 \cos θ$ to $\tan θ .$ $\tan θ .$
In Example 2, change $2 \cos^{2} x$ $2 \cos^{2} x$ to $2 \sin^{2} x .$ $2 \sin^{2} x .$
In Example 4, change $\cos \frac{1}{2} x$ $\cos \frac{1}{2} x$ to $\sin \frac{1}{2} x$ $\sin \frac{1}{2} x$ and on the right of the equal sign change the $+$ $+$ to $- .$ $- .$
In Example 7, change the $+$ $+$ to $- .$ $- .$

In Exercises 5–20, solve the given trigonometric equations analytically (using identities when necessary for exact values when possible) for values of x for $0 \leq x < 2 π .$ $0 \leq x < 2 π .$

$\sin x - 1 = 0$ $\sin x - 1 = 0$
$2 \cos x + 1 = 0$ $2 \cos x + 1 = 0$
$1 - 2 \cos x = 0$ $1 - 2 \cos x = 0$
$4 \tan x + 2 = 3 (1 + \tan x)$ $4 \tan x + 2 = 3 (1 + \tan x)$
$4 - \sec^{2} x = 0$ $4 - \sec^{2} x = 0$
$3 \tan x - \cot x = 0$ $3 \tan x - \cot x = 0$
$2 \sin^{2} x - \sin x = 0$ $2 \sin^{2} x - \sin x = 0$
$\sin 4 x - \sin 2 x = 0$ $\sin 4 x - \sin 2 x = 0$
$\sin 2 x \sin x + \cos x = 0$ $\sin 2 x \sin x + \cos x = 0$
$\sin x - \sin \frac{x}{2} = 0$ $\sin x - \sin \frac{x}{2} = 0$
$2 \cos^{2} x - 2 \cos 2 x - 1 = 0$ $2 \cos^{2} x - 2 \cos 2 x - 1 = 0$
$\csc^{2} x + 2 = 3 \csc x$ $\csc^{2} x + 2 = 3 \csc x$
$4 \tan x - \sec^{2} x = 0$ $4 \tan x - \sec^{2} x = 0$
$\sin (x - \frac{π}{4}) = \cos (x - \frac{π}{4})$ $\sin (x - \frac{π}{4}) = \cos (x - \frac{π}{4})$
$\sin 2 x \cos x - \cos 2 x \sin x = 0$ $\sin 2 x \cos x - \cos 2 x \sin x = 0$
$\cos 3 x \cos x - \sin 3 x \sin x = 0$ $\cos 3 x \cos x - \sin 3 x \sin x = 0$

In Exercises 21–38, solve the given trigonometric equations analytically and by use of a calculator. Compare results. Use values of x for $0 \leq x < 2 π .$ $0 \leq x < 2 π .$

$\tan x + 1 = 0$ $\tan x + 1 = 0$
$2 \sin x + 1 = 0$ $2 \sin x + 1 = 0$
$3 - 4 \cos x = 7 - (2 - \cos x)$ $3 - 4 \cos x = 7 - (2 - \cos x)$
$7 \sin x - 2 = 3 (2 - \sin x)$ $7 \sin x - 2 = 3 (2 - \sin x)$
$4 - 3 \csc^{2} x = 0$ $4 - 3 \csc^{2} x = 0$
$| \sin x | = \frac{1}{2}$ $| \sin x | = \frac{1}{2}$
$\sin 4 x - \cos 2 x = 0$ $\sin 4 x - \cos 2 x = 0$
$3 \cos x - 4 \cos^{2} x = 0$ $3 \cos x - 4 \cos^{2} x = 0$
$2 \sin x = \tan x$ $2 \sin x = \tan x$
$\cos 2 x + \sin^{2} x = 0$ $\cos 2 x + \sin^{2} x = 0$
$\sin^{2} x - 2 \sin x = 1$ $\sin^{2} x - 2 \sin x = 1$
$2 \cos^{2} 2 x + 1 = 3 \cos 2 x$ $2 \cos^{2} 2 x + 1 = 3 \cos 2 x$
$\tan x + 3 \cot x = 4$ $\tan x + 3 \cot x = 4$
$\tan^{2} x + 4 = {2 sec}^{2} x$ $\tan^{2} x + 4 = {2 sec}^{2} x$
$\sin 2 x + \cos 2 x = 0$ $\sin 2 x + \cos 2 x = 0$
$2 \sin 4 x + \csc 4 x = 3$ $2 \sin 4 x + \csc 4 x = 3$
$2 \sin 2 x - {\cos x \sin}^{3} x = 0$ $2 \sin 2 x - {\cos x \sin}^{3} x = 0$
$\sec^{4} x = \csc^{4} x$ $\sec^{4} x = \csc^{4} x$

In Exercises 39–54, solve the indicated equations analytically.

$\sin 3 x + \sin x = 0$ $\sin 3 x + \sin x = 0$ [Hint: See Eq. (20.17).]
$\cos 3 x - \cos x = 0$ $\cos 3 x - \cos x = 0$ [Hint: See Eq. (20.20).]
Is there any positive acute angle $θ$ $θ$ for which $\sin θ + \cos θ + \tan θ + \cot θ + \sec θ + \csc θ = 1 ?$ $\sin θ + \cos θ + \tan θ + \cot θ + \sec θ + \csc θ = 1 ?$ Explain.
Use a calculator to determine the minimum value of the function to the left of the equal sign in Exercise 41 (for a positive acute angle).
Solve the system of equations $r = \sin θ, r = \sin 2 θ,$ $r = \sin θ, r = \sin 2 θ,$ for $0 \leq θ < 2 π .$ $0 \leq θ < 2 π .$
Solve the system of equations $r = \sin θ, r = \cos 2 θ,$ $r = \sin θ, r = \cos 2 θ,$ for $0 \leq θ < 2 π .$ $0 \leq θ < 2 π .$
Find the angles of a triangle if one side is twice another side and the angles opposite these sides differ by $60 °$ $60 °$ .
If two musical tones of frequencies 220 Hz and 223 Hz are played together, beats will be heard. This can be represented by $y = \sin 440 π t + \sin 446 π t .$ $y = \sin 440 π t + \sin 446 π t .$ Graph this function and estimate t (in s) when $y = 0$ $y = 0$ between beats for $0.15 < t < 1.15 s .$ $0.15 < t < 1.15 s .$
The acceleration due to gravity g (in $m / s^{2}$ $m / s^{2}$ ) varies with latitude, approximately given by $g = 9.7805 (1 + 0.0053 \sin^{2} θ),$ $g = 9.7805 (1 + 0.0053 \sin^{2} θ),$ where $θ$ $θ$ is the latitude in degrees. Find $θ$ $θ$ for $g = 9.8000 .$ $g = 9.8000 .$
Under certain conditions, the electric current i (in A) in the circuit shown in Fig. 20.33 is given below. For what value of t (in s) is the current first equal to zero?

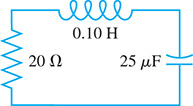
Fig. 20.33

$i = - e^{- 100 t} (32.0 \sin 624.5 t + 0.200 \cos 624.5 t)$ $i = - e^{- 100 t} (32.0 \sin 624.5 t + 0.200 \cos 624.5 t)$
The vertical displacement y (in m) of the end of a robot arm is given by $y = 2.30 \cos 0.1 t - 1.35 \sin 0.2 t .$ $y = 2.30 \cos 0.1 t - 1.35 \sin 0.2 t .$ Find the first four values of t (in s) for which $y = 0 .$ $y = 0 .$
In finding the maximum illuminance from a point source of light, it is necessary to solve the equation $\cos θ \sin 2 θ - \sin^{3} θ = 0 .$ $\cos θ \sin 2 θ - \sin^{3} θ = 0 .$ Find $θ$ $θ$ if $0 < θ < 90 ° .$ $0 < θ < 90 ° .$
To find the angle $θ$ $θ$ subtended by a certain object on a camera film, it is necessary to solve the equation $\frac{p^{2} \tan θ}{0.0063 + p \tan θ} = 1.6,$ $\frac{p^{2} \tan θ}{0.0063 + p \tan θ} = 1.6,$ where p is the distance from the camera to the object. Find $θ$ $θ$ if $p = 4.8 m .$ $p = 4.8 m .$
The velocity of a certain piston is maximum when the acute crank angle $θ$ $θ$ satisfies the equation $8 \cos θ + \cos 2 θ = 0 .$ $8 \cos θ + \cos 2 θ = 0 .$ Find this angle.
Resolve a force of 500.0 N into two components, perpendicular to each other, for which the sum of their magnitudes is 700.0 N, by using the angle between a component and the resultant.
Looking for a lost ship in the North Atlantic Ocean, a plane flew from Reykjavik, Iceland, 160 km west. It then turned and flew due north and then made a final turn to fly directly back to Reykjavik. If the total distance flown was 480 km, how long were the final two legs of the flight? Solve by setting up and solving an appropriate trigonometric equation. (The Pythagorean theorem may be used only as a check.)

In Exercises 55–62, solve the given equations graphically.

$3 \sin x - x = 0$ $3 \sin x - x = 0$
$4 \cos x + 3 x = 0$ $4 \cos x + 3 x = 0$
$2 \sin 2 x = x^{2} + 1$ $2 \sin 2 x = x^{2} + 1$
$\sqrt{x} - \sin 3 x = 1$ $\sqrt{x} - \sin 3 x = 1$
$2 \ln x = 1 - \cos 2 x$ $2 \ln x = 1 - \cos 2 x$
$e^{x} = 1 + \sin x$ $e^{x} = 1 + \sin x$
In finding the frequencies of vibration of a vibrating wire, the equation $x \tan x = 2.00$ $x \tan x = 2.00$ occurs. Find x if $0 < x < π / 2 .$ $0 < x < π / 2 .$
An equation used in astronomy is $θ - e \sin θ = M .$ $θ - e \sin θ = M .$ Solve for $θ$ $θ$ for $e = 0.25$ $e = 0.25$ and $M = 0.75 .$ $M = 0.75 .$

Answers to Practice Exercises

$x = 7 π / 6, 11 π / 6$ $x = 7 π / 6, 11 π / 6$
$x = 3 π / 4, 7 π / 4$ $x = 3 π / 4, 7 π / 4$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 20.5 Solving Trigonometric Equations

Create new playlist

Sign In

Sign Up

Table of Contents for
20.5 Solving Trigonometric Equations