16.6 Higher-order Determinants

  • Minors • Expansion by Minors • Properties of Determinants • Solving Systems of Equations

In Chapter 5, we limited our discussion of determinants to those of the second and third orders. We now show some methods of evaluating higher-order determinants, and use these methods to solve systems of equations.

From Section 5.7, we recall the definition of a third-order determinant. By rearranging the terms and factoring out a1 ,  − a2 ,  and a3 ,  we have

 | a1b1c1a2b2c2a3b3c3 |  = a1b2c3 + a3b1c2 + a2b3c1 − a3b2c1 − a1b3c2 − a2b1c3 = a1(b2c3 − b3c2) − a2(b1c3 − b3c1) + a3(b1c2 − b2c1) = a1 | b2c2b3c3 |  − a2 | b1c1b3c3 |  + a3 | b1c1b2c2 | 
(16.12)

In Eq. (16.12), the third-order determinant is expanded as products of the elements of the first column and second-order determinants, known as minors. In general, the minor of an element of a determinant is the determinant that results by deleting the row and column in which the element lies.

EXAMPLE 1 Minors

A determinant.

Equation (16.12) is only one way of expressing the expansion of the third-order determinant, but it does lead to a general theorem for the expansion of a determinant of any order. It is not a proof of the following theorem, but does provide a basis for it.

EXPANSION OF A DETERMINANT BY MINORS

The value of a determinant of order n may be found by forming the n products of the elements of any column (or row) and their minors. A product is given a plus sign if the sum of the number of the column and the number of the row in which the element lies is even, and a minus sign if this sum is odd. (See the sign chart in Fig. 16.19.) The algebraic sum of these terms is the value of the determinant.

NOTE

[Since we can expand by any row or column, we usually choose one that has one or more zeros in order to make the calculations easier.]

A sign chart for the expansion row or column in a determinant. Row 1: plus, minus, plus, and so on. Row 2: minus, plus, minus, and so on. Row 3: plus, minus, plus, and so on. This pattern continues.

Fig. 16.19

EXAMPLE 2 Expansion by minors

In evaluating the following determinant, note that the third column has two zeros. This means that expanding by the third column will require less numerical work. Therefore,

Process of determinant matrices evaluation.

As we noted in Chapter 5, most calculators can be used to quickly evaluate determinants. Figure 16.20 shows the calculator evaluation of this determinant.

A calculator screen.

Fig. 16.20

Graphing calculator keystrokes: bit.ly/2Ceb7QR

PROPERTIES OF DETERMINANTS

We now state some properties which allow us to find certain determinants quickly and to see how certain changes to a matrix affect the value of the determinant.

  1. If each element above or each element below the principal diagonal of a determinant is zero, then the product of the elements of the principal diagonal is the value of the determinant.

  2. If all corresponding rows and columns of a determinant are interchanged, the value of the determinant is unchanged.

  3. If two columns (or rows) of a determinant are identical, the value of the determinant is zero.

  4. If two columns (or rows) of a determinant are interchanged, the value of the determinant is changed in sign.

  5. If all elements of a column (or row) are multiplied by the same number k, the value of the determinant is multiplied by k.

  6. If all the elements of any column (or row) are multiplied by the same number k, and the resulting numbers are added to the corresponding elements of another column (or row), the value of the determinant is unchanged.

EXAMPLE 3 Using properties of determinants

  1.  | 2180 − 5900 − 6 |  = 2( − 5)( − 6) = 60property 1

  2. Property 3. A 3 by 3 matrix = 0, The row entries of matrix are as follows. Row 1. 3, 5, 2. Row 2. negative 4, 6, 9. Row 3. negative 4, 6, 9.

  3.  |  − 10663 − 6053 |  = 3 |  − 10621 − 2053 | property 5the value of the first is 141,and the value of the second is 47141= 3( 47) 

The properties given here can be used to simplify the evaluation of determinants using expansion by minors. For example, property 6 can be used to get all zeros under the principal diagonal. Then, by property 1, the determinant is the product of the elements of the principal diagonal. However, due to the ability of calculators and computers to evaluate determinants, this is not as necessary as it was in the past.

SOLVING SYSTEMS OF LINEAR EQUATIONS BY DETERMINANTS

We can use the expansion of determinants by minors to solve systems of linear equations. Cramer’s rule for solving systems of linear equations, as stated in Section 5.6, is valid for any system of n equations in n unknowns.

EXAMPLE 4 Solving a system of four equations

Solve the following system of equations:

x + 2y + z = 52x + z + 2t = 1x − y + 3z + 4t =  − 64x − y − 2t = 0
An illustration of determinant over determinant process.

Note that we chose to expand the determinant in the numerator by the fourth row since it contains two zeros. In the denominator, we expanded by the first row since it contains a zero, and no other row or column contains more than one zero.

In solving for y, we again note the two zeros in the fourth row:

y =  | 151021121 − 634400 − 2 | 54 =  − 4 | 510112 − 634 |  + ( − 2) | 1512111 − 63 | expanding by fourth row54 =  − 4( − 26) − 2( − 29)54 = 104 + 5854 = 16254 = 3

Substituting x = 1 and y = 3 in the first equation gives us z =  − 2. Then substituting x = 1 and y = 3 in the fourth equation gives us t = 1/2. Therefore, the required solution is x = 1 , y = 3 , z =  − 2 , t = 1/2. We can check the solution by substituting in the second or third equation (we used the first and fourth to find values of z and t.)

EXERCISES 16.6

In Exercises 1 and 2, make the given changes in the indicated examples of this section. Then evaluate the resulting determinants.

  1. In Example 2, change the  − 2 in the first row to 0 and then find the determinant.

  2. In Example 3(a), change the 2 in the first row to a 3 and then find the determinant.

In Exercises 3–6, evaluate each determinant by inspection. Observation will allow evaluation by using the properties of this section.

  1.  | 10 − 5803 − 800 − 3 | 

  2.  |  − 3000100 − 9 − 1 − 5 | 

  3.  | 3 − 2425 − 12 − 13 − 24203 − 60 | 

  4.  |  − 12 − 24 − 2415123232 − 35 − 221818184400 − 26 | 

In Exercises 7–10, use the given value of the determinant at the right and the properties of this section to evaluate the following determinants.

 | 2 − 31 − 4131 − 3 − 2 |  = 40

  1.  | 21 − 3 − 4311 − 2 − 3 | 

  2.  | 2 − 31 − 4132 − 6 − 4 | 

  3.  | 2 − 33 − 4191 − 3 − 6 | 

  4.  | 2 − 41 − 31 − 313 − 2 | 

In Exercises 11–20, evaluate the given determinants by expansion by minors.

  1.  | 200 − 2144 − 23 | 

  2.  | 100 − 3 − 2 − 41302 | 

  3.  | 310 − 23 − 1425 | 

  4.  |  − 4030 − 20 − 8816 − 1575 − 45 | 

  5.  | 4360300450122117 | 

  6.  | 6 − 3 − 63 − 212 − 1187 − 150 − 11010 | 

  7.  | 5305421232 − 22012 − 1 | 

  8.  |  − 2213143143 − 2 − 23 − 215 | 

  9.  | 120100210110 − 11 − 1 − 20 − 121102 − 1 − 2 | 

  10.  |  − 1350 − 50173 − 25 − 2 − 103 − 302 − 13621 − 42 | 

In Exercises 21–24, solve the given systems of equations by determinants. Evaluate by expansion by minors.

  1. 2x + 2t = 03x + y + z =  − 12y − z + 3t = 12z − 3t = 1

  2. 2x + y + z = 42y − 2z − t = 33y − 3z + 2t = 16x − y + t = 0

  3. x + 2y − z = 6y − 2z − 3t =  − 53x − 2y + t = 22x + y + z − t = 0

  4. 2p + 3r + s = 4p − 2r − 3s + 4t =  − 13p + r + s − 5t = 3 − p + 2r + s + 3t = 2

In Exercises 25–28, solve the given systems of equations by determinants. Evaluate by using a calculator.

  1. 2x + y + z = 23y − z + 2t = 4y + 2z + t = 03x + 2z = 4

  2. 6x + 3y + 3z = 0x − y + 2t = 22y + z + 4t = 25x + 2z + 2t = 4

  3. D + E + 2F = 12D − E + G =  − 2D − E − F − 2G = 42D − E + 2F − G = 0

  4. 3x + y + t = 03z + 2t = 86x + 2y + 2z + t = 33x − y − z − t = 0

In Exercises 29–32, make the indicated changes in the determinant at the right, and then solve the indicated problem. Assume the elements are nonzero, unless otherwise specified.

 | abcdefghi | 

  1. Evaluate the determinant if a = c , d = f ,  and g = i . 

  2. Evaluate the determinant if b = c = f = 0.

  3. By what factor is the value of the determinant changed if all elements are doubled?

  4. How is the value changed if a is added to g, b added to h, and c added to i?

In Exercises 33–38, solve the given problems by using determinants.

  1. In applying Kirchhoff’s laws (see Example 2 on page 141) to the circuit shown in Fig. 16.21, the following equations are found. Determine the indicated currents (in A).

    A circuit.

    Fig. 16.21

    IA + IB + IC + ID + IE = 0 − 2IA + 3IB = 03IB − 3IC = 6 − 3IC + ID = 0 − ID + 2IE = 0

  2. In analyzing the forces A, B, C, and D shown on the beam in Fig. 16.22, the following equations are used. Find these forces.

    A + B = 850A + B + 400 = 0.8C + 0.6D0.6C = 0.8D5A − 5B + 4C − 3D = 0
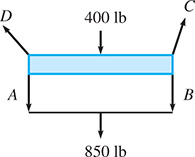
    Forces on a beam.

    Fig. 16.22

  3. The area of a triangle with vertices (x1 , y1) , (x2 , y2) ,  and (x3 , y3) is given by A =  ± 12 | x1y11x2y21x3y31 |  .  (If the answer comes out negative, take the absolute value). A natural gas company locates the three corners of a triangular-shaped shale natural gas reserve at (0,0), (8.45, 3.64), and (1.82, 5.70), where all measurements are in kilometers. Find the area of the reserve.

  4. An alloy is to be made from four other alloys containing copper (Cu), nickel (Ni), zinc (Zn), and iron (Fe). The first is 80% Cu and 20% Ni. The second is 60% Cu, 20% Ni, and 20% Zn. The third is 30% Cu, 60% Ni, and 10% Fe. The fourth is 20% Ni, 40% Zn, and 40% Fe. How much of each is needed so that the final alloy has 56 g Cu, 28 g Ni, 10 g Zn, and 6 g Fe?

  5. In testing for air pollution, a given air sample contained a total of 6.0 parts per million (ppm) of four pollutants, sulfur dioxide (SO2) ,  nitric oxide (NO), nitrogen dioxide (NO2) ,  and carbon monoxide (CO). The ppm of CO was 10 times that of SO2 ,  which in turn equaled those of NO and NO2 .  There was a total of 0.8 ppm of SO2 and NO. How many ppm of each were present in the air sample?

  6. A tablet with a 32-GB hard drive starts out with three different apps A, B, and C, which use up 4% of the tablet’s memory. Two more apps are added, each using the same amount of memory as app A, and the apps then use a total of 6% of the tablet’s memory. Then, in addition to those, three more apps requiring the same memory as app B are added. All eight apps combined use up 13.5% of the tablet’s memory. Find the number of megabytes (MB) of memory required for each app A, B, and C. (1 GB = 1000 MB . )

Answers to Practice Exercises

  1. 135

  2. x = 1 , y = 2 , z =  − 3 , t = 1

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.22.100.180