10.4 Graphs of y = tan x , y = cot x , y = sec x , y = csc x

  • Graph of y = tanx • Reciprocal Functions • Asymptotes • Graphs of y = cot x ,  y = secx ,  y = cscx

The graph of y = tan x is displayed in Fig. 10.23. Because from Section 4.3 we know that csc x  = 1 / sin x ,  sec x  = 1 / cos x ,  and cot x  = 1 / tan x ,  we are able to find values of y = csc x ,  y = sec x ,  and y = cot x and graph these functions, as shown in Figs. 10.24–10.26.

The graph is y = tangent of x.

Fig. 10.23

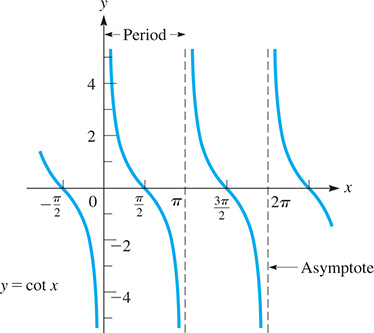
The graph is y = cotangent of x.

Fig. 10.24

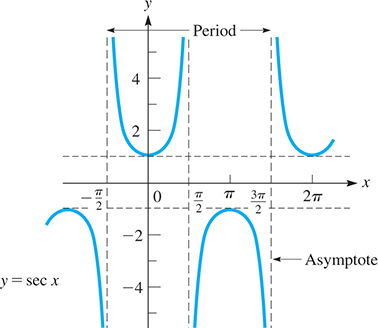
The graph is y = secant of x.

Fig. 10.25

The graph is y = cosecant of x.

Fig. 10.26

From these graphs, note that the period for y = tan x and y = cot x is π ,  and that the period of y = sec x and y = csc x is 2π .  The vertical dashed lines are asymptotes (see Sections 3.4 and 21.6). The curves approach these lines, but never actually reach them.

The functions are not defined for the values of x for which the curve has asymptotes. This means that the domains do not include these values of x. Thus, we see that the domains of y = tan x and y = sec x include all real numbers, except the values x =  − π / 2 ,  π / 2 ,  3π / 2 ,  and so on. The domain of y = cot x and y = csc x include all real numbers except x =  − π ,  0 ,  π ,  2π ,  and so on.

From the graphs, we see that the ranges of y = tan x and y = cot x are all real numbers, but that the ranges of y = sec x and y = csc x do not include the real numbers between  − 1 and 1.

To sketch functions such as y = a sec x ,  first sketch y = sec x and then multiply the y-values by a.

NOTE

[Here, a is not an amplitude, because the ranges of these functions are not limited in the same way they are for the sine and cosine functions.]

Example 1 Sketching graph of y = a sec x

Sketch the graph of y = 2 sec x . 

First, we sketch in y = sec x ,  the curve shown in black in Fig. 10.27. Then we multiply the y-values of this secant function by 2. Although we can only estimate these values and do this approximately, a reasonable graph can be sketched this way. The desired curve is shown in blue in Fig. 10.27.

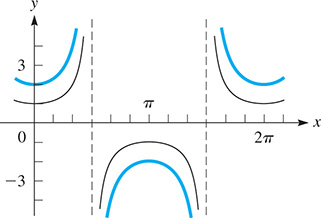
The graph is sketched.

Fig. 10.27

Using a calculator, we can display the graphs of these functions more easily and more accurately than by sketching them. By knowing the general shape and period of the function, the values for the window settings can be determined.

Example 2 Calculator graph of y = a cot bx

View at least two cycles of the graph of y = 0.5 cot 2x on a calculator.

Because the period of y = cot x is π ,  the period of y = cot 2x is π / 2 .  Therefore, we choose the window settings as follows:

  • Xmin = 0(x = 0 is one asymptote of the curve)Xmax = π(the period is π / 2 ;  two periods is π)Ymin =  − 5 ,  Ymax = 5(the range is all x ;  this shows enough of the curve)

We must remember to enter the function as y1 = 0.5(tan 2x) − 1 ,  because cot x  = (tan x) − 1 .  The graphing calculator view is shown in Fig. 10.28. We can view many more cycles of the curve with appropriate window settings.

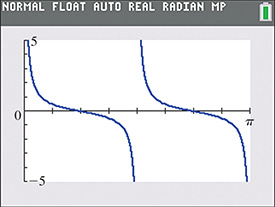
The graph is periodic about the x-axis.

Fig. 10.28

Example 3 Calculator graph of y = a csc(bx + c)

View at least two periods of the graph of y = 2 csc(2x + π / 4) on a calculator.

Because the period of csc x is 2π ,  the period of csc(2x + π / 4) is 2π / 2 = π .  Recalling that csc x  = (sin x) − 1 ,  the curve will have the same displacement as y = sin(2x + π / 4) .  Therefore, displacement is  − π / 42 =  − π8 .  There is some flexibility in choosing the window settings, and as an example, we choose the following settings.

  • Xmin =  − 0.5(the displacement is  − π / 8 =  − 0.4)Xmax = 6(displacement =  − π / 8 ;  period = π ,   − π / 8 + 2π = 15π / 8 = 5.9)Ymin =  − 6 ,  Ymax = 6(there is no curve between y =  − 2 and y = 2)

With y1 = 2[ sin(2x + π / 4)]  − 1 ,  the function is graphed in blue in Fig. 10.29. The graph of y = 2 sin(2x + π / 4) is shown in red for reference.

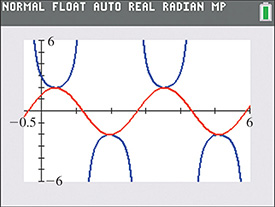
Two graphs.

Fig. 10.29

Exercises 10.4

In Exercises 1 and 2, view the graphs on a calculator if the given changes are made in the indicated examples of this section.

  1. In Example 2, change 0.5 to 5.

  2. In Example 3, change the sign before π / 4 . 

In Exercises 3–6, fill in the following table for each function and plot the graph from these points.

x  − π2  − π3  − π4  − π6 0 π6 π4 π3 π2 2π3 3π4 5π6 π y

  1. y = tan x

  2. y = cot x

  3. y = sec x

  4. y = csc x

In Exercises 7–14, sketch the graphs of the given functions by use of the basic curve forms (Figs. 10.23, 10.24, 10.25, and 10.26). See Example 1.

  1. y = 2 tan x

  2. y = 3 cot x

  3. y = 12sec x

  4. y = 32csc x

  5. y =  − 8 cot x

  6. y =  − 0.1 tan x

  7. y =  − 3 csc x

  8. y =  − 60 sec x

In Exercises 15–24, view at least two cycles of the graphs of the given functions on a calculator.

  1. y = tan 2x

  2. y = 2 cot 3x

  3. y = 12sec 3x

  4. y =  − 0.4 csc 2x

  5. y =  − 2 cot(2x + π6)

  6. y = tan(3x − π2)

  7. y = 18 csc(3x − π3)

  8. y = 12sec(2x + π4)

  9. y = 75 tan(0.5x − π16)

  10. y = 0.5 sec(0.2x + π25)

In Exercises 25–28, solve the given problems. In Exercises 29–32, sketch the appropriate graphs, and check each on a calculator.

  1. Using the graph of y = tan x ,  explain what happens to tan x as x gets closer to π / 2 (a) from the left and (b) from the right.

  2. Using a calculator, graph y = sin x and y = csc x in the same window. When sin x reaches a maximum or minimum, explain what happens to csc x.

  3. Write the equation of a secant function with zero displacement, a period of 4π ,  and that passes through (0 ,  − 3) . 

  4. Use a graphing calculator to show that sin x  < tan x for 0 < x < π / 2 ,  although sin x and tan x are nearly equal for the values near zero.

  5. Near Antarctica, an iceberg with a vertical face 200 m high is seen from a small boat. At a distance x from the iceberg, the angle of elevation θ of the top of the iceberg can be found from the equation x = 200 cot θ .  Sketch x as a function of θ . 

  6. In a laser experiment, two mirrors move horizontally in equal and opposite distances from point A. The laser path from and to point B is shown in Fig. 10.30. From the figure, we see that x = a tan θ .  Sketch the graph of x = f(θ) for a = 5.00 cm . 

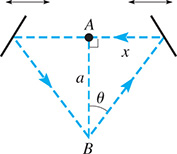
    A diagram of lasers that form a triangle with vertex B and altitude ay that goes to point upper Ay. The altitude is at angle theta at angle B. Opposite this angle is side x.

    Fig. 10.30

  7. A mechanism with two springs is shown in Fig. 10.31, where point A is restricted to move horizontally. From the law of sines, we see that b = (a sin B) csc A .  Sketch the graph of b as a function of A for a = 4.00 cm and B = π / 4 . 

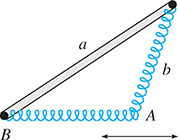
    An object and two springs form a triangle. The springs meet at angle Ay, and the object is opposite side ay. Opposite angle B is side b along one of the springs.

    Fig. 10.31

  8. A cantilever column of length L will buckle if too large a downward force P is applied d units off center. The horizontal deflection x (see Fig. 10.32) is x = d[ sec(kL) − 1]  ,  where k is a constant depending on P, and 0 < kL < π / 2 .  For a constant d, sketch the graph of x as a function of kL.

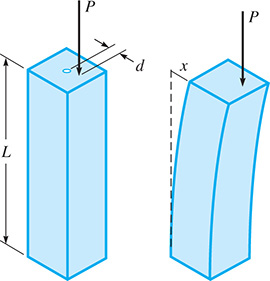
    A rectangular solid with length L has force P applied at its top, d units from the center. The solid deflects a horizontal distance of x.

    Fig. 10.32

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.139.107.241