Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

21.10 Polar Coordinates

Pole • Polar Axis • Polar Coordinates • Converting Between Polar and Rectangular Coordinates

To this point, we have graphed all curves in the rectangular coordinate system. However, for certain types of curves, other coordinate systems are better adapted. We discuss one of these systems here.

Instead of designating a point by its x- and y-coordinates, we can specify its location by its radius vector and the angle the radius vector makes with the x-axis. Thus, the r and $θ$ $θ$ that are used in the definitions of the trigonometric functions can also be used as the coordinates of points in the plane. The important aspect of choosing coordinates is that, for each set of values, there must be only one point that corresponds to this set. We can see that this condition is satisfied by the use of r and $θ$ $θ$ as coordinates. In polar coordinates, the origin is called the pole, and the half-line for which the angle is zero (equivalent to the positive x-axis) is called the polar axis. The coordinates of a point are designated as $(r, θ) .$ $(r, θ) .$ We will use radians when measuring the value of $θ .$ $θ .$ See Fig. 21.101.

An angle with polar coordinates. — Fig. 21.101

Figure 21.101 Full Alternative Text

When using polar coordinates, we generally label the lines for some of the values of $θ;$ $θ;$ namely, those for $θ = 0$ $θ = 0$ (the polar axis), $θ = π / 2$ $θ = π / 2$ (equivalent to the positive y-axis), $θ = π$ $θ = π$ (equivalent to the negative x-axis), $θ = 3 π / 2$ $θ = 3 π / 2$ (equivalent to the negative y-axis), and possibly others. In Fig. 21.102, these lines and those for multiples of $π / 6$ $π / 6$ are shown. Also, the circles for $r = 1, r = 2,$ $r = 1, r = 2,$ and $r = 3$ $r = 3$ are shown in this figure.

Graphs of concentric circles. — Fig. 21.102

Figure 21.102 Full Alternative Text

EXAMPLE 1 Polar coordinates of a point

If $r = 2$ $r = 2$ and $θ = π / 6,$ $θ = π / 6,$ we have the point shown in Fig. 21.103 . The point corresponds to $(\sqrt{3}, 1)$ $(\sqrt{3}, 1)$ in rectangular coordinates.

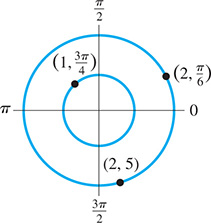
Fig. 21.103

Figure 21.103 Full Alternative Text
The polar coordinate point $(1, 3 π / 4)$ $(1, 3 π / 4)$ is also shown. It is equivalent to $(- \sqrt{2} / 2, \sqrt{2} / 2)$ $(- \sqrt{2} / 2, \sqrt{2} / 2)$ in rectangular coordinates.
The polar coordinate point (2, 5) is also shown. It is equivalent approximately to $(0.6, - 1.9)$ $(0.6, - 1.9)$ in rectangular coordinates. Remember, the 5 is an angle in radians.

One difference between rectangular coordinates and polar coordinates is that, for each point in the plane, there are limitless possibilities for the polar coordinates of that point. For example, the point $(2, \frac{π}{6})$ $(2, \frac{π}{6})$ can also be represented by $(2, \frac{13 π}{6})$ $(2, \frac{13 π}{6})$ because the angles $\frac{π}{6}$ $\frac{π}{6}$ and $\frac{13 π}{6}$ $\frac{13 π}{6}$ are coterminal. We also remove one restriction on r that we imposed in the definition of the trigonometric functions. That is, r is allowed to take on positive and negative values.

NOTE

[If r is negative, $θ$ $θ$ is located as before, but the point is found r units from the pole on the opposite side from that on which it is positive.]

EXAMPLE 2 Polar coordinates—negative `r`

The polar coordinates $(3, 2 π / 3)$ $(3, 2 π / 3)$ and $(3, - 4 π / 3)$ $(3, - 4 π / 3)$ represent the same point. However, the point $(- 3, 2 π / 3)$ $(- 3, 2 π / 3)$ is on the opposite side of the pole from $(3, 2 π / 3),$ $(3, 2 π / 3),$ 3 units from the pole. Another possible set of polar coordinates for the point $(- 3, 2 π / 3)$ $(- 3, 2 π / 3)$ is $(3, 5 π / 3) .$ $(3, 5 π / 3) .$ These points are shown in Fig. 21.104.

The graphs of 3 concentric circles centered at the pole. — Fig. 21.104

Figure 21.104 Full Alternative Text

NOTE

[When locating and plotting a point in polar coordinates, it is generally best to first locate the terminal side of $θ,$ $θ,$ and then measure r along this terminal side.]

This is illustrated in the following example.

EXAMPLE 3 Locate the terminal side first

Plot the points $A (2, 5 π / 6)$ $A (2, 5 π / 6)$ and $(- 3.2, - 2.4)$ $(- 3.2, - 2.4)$ in the polar coordinate system.

To locate A, we determine the terminal side of $θ = 5 π / 6$ $θ = 5 π / 6$ and then determine $r = 2.$ $r = 2.$ See Fig. 21.105.

To locate B, we find the terminal side of $θ = - 2.4,$ $θ = - 2.4,$ measuring clockwise from the polar axis (and recalling that $π = 3.14 = 180 °$ $π = 3.14 = 180 °$ ). Then we locate $r = - 3.2$ $r = - 3.2$ on the opposite side of the pole. See Fig. 21.105.

A polar coordinate system. — Fig. 21.105

Figure 21.105 Full Alternative Text

We will find that points with negative values of r occur frequently when plotting curves in polar coordinates.

POLAR AND RECTANGULAR COORDINATES

The relationships between the polar coordinates of a point and the rectangular coordinates of the same point come from the definitions of the trigonometric functions. Those most commonly used are (see Fig. 21.106)

Figure 21.106 Full Alternative Text

x = r \cos θ y = r \sin θ

$x = r \cos θ y = r \sin θ$ (21.41)

\tan θ = \frac{y}{x} r = \sqrt{x^{2} + y^{2}}

$\tan θ = \frac{y}{x} r = \sqrt{x^{2} + y^{2}}$ (21.42)

The following examples show the use of Eqs. (21.41) and (21.42) in changing coordinates in one system to coordinates in the other system. Also, these equations are used to transform equations from one system to the other.

EXAMPLE 4 Polar to rectangular coordinates

Using Eqs. (21.41), we can transform the polar coordinates $(4, π / 4)$ $(4, π / 4)$ into the rectangular coordinates $(2 \sqrt{2}, 2 \sqrt{2}),$ $(2 \sqrt{2}, 2 \sqrt{2}),$ because

x = 4 \cos \frac{π}{4} = 4 (\frac{\sqrt{2}}{2}) = 2 \sqrt{2} and y = 4 \sin \frac{π}{4} = 4 (\frac{\sqrt{2}}{2}) = 2 \sqrt{2}

$x = 4 \cos \frac{π}{4} = 4 (\frac{\sqrt{2}}{2}) = 2 \sqrt{2} and y = 4 \sin \frac{π}{4} = 4 (\frac{\sqrt{2}}{2}) = 2 \sqrt{2}$

See Fig. 21.107.

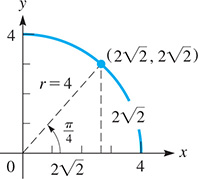
A curve falls from (0, 4) through (2 times square root of 2, 2 times square root of 2) to (4, 0). — Fig. 21.107

Figure 21.107 Full Alternative Text

EXAMPLE 5 Rectangular to polar coordinates

Using Eqs. (21.42), we can transform the rectangular coordinates $(3, - 5)$ $(3, - 5)$ into polar coordinates, as follows.

\begin{array}{rcl} \tan θ & = & - \frac{5}{3}, θ = 5.25 (or - 1.03) \\ r & = & \sqrt{3^{2} + {(- 5)}^{2}} = 5.83 \end{array}

$\begin{array}{rcl} \tan θ & = & - \frac{5}{3}, θ = 5.25 (or - 1.03) \\ r & = & \sqrt{3^{2} + {(- 5)}^{2}} = 5.83 \end{array}$

We know that $θ$ $θ$ is a fourth-quadrant angle because x is positive and y is negative. Therefore, the point $(3, - 5)$ $(3, - 5)$ in rectangular coordinates can be expressed as the point (5.83, 5.25) in polar coordinates (see Fig. 21.108). Other polar coordinates for the point are also possible.

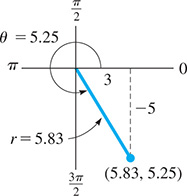
A position angle with terminal side r = 5.83 at angle theta = 5.25. The terminal side goes to (5.83, 5.25) with horizontal length 3 and vertical length negative 5 in quadrant 4. — Fig. 21.108

Calculators are programmed to make conversions between rectangular and polar coordinates. The display for the conversions of Examples 4 and 5 are shown in Fig. 21.109.

A calculator screen. — Fig. 21.109

Graphing calculator keystrokes: bit.ly/2CGNuB8

Figure 21.109 Full Alternative Text

EXAMPLE 6 Rectangular to polar equation—particle accelerator

If an electrically charged particle enters a magnetic field at right angles to the field, the particle follows a circular path. This fact is used in the design of nuclear particle accelerators.

A proton (positively charged) enters a magnetic field such that its path may be described by the rectangular equation $x^{2} + y^{2} = 2 x,$ $x^{2} + y^{2} = 2 x,$ where measurements are in meters. Find the polar equation of this circle.

We change this equation expressed in the rectangular coordinates x and y into an equation expressed in the polar coordinates r and $θ$ $θ$ by using the relations $r^{2} = x^{2} + y^{2}$ $r^{2} = x^{2} + y^{2}$ and $x = r \cos θ$ $x = r \cos θ$ as follows:

\begin{array}{rcl} x^{2} + y^{2} & = & 2 x & rectangular equation \\ r^{2} & = & 2 r \cos θ & substitute \\ r & = & 2 \cos θ & divided by r \end{array}

$\begin{array}{rcl} x^{2} + y^{2} & = & 2 x & rectangular equation \\ r^{2} & = & 2 r \cos θ & substitute \\ r & = & 2 \cos θ & divided by r \end{array}$

This is the polar equation of the circle, which is shown in Fig. 21.110.

A circle centered at (1, 0) with radius r = 2 cosine of theta. A point on the circle is in quadrant 1, and the circle rotates clockwise. — Fig. 21.110

EXAMPLE 7 Polar to rectangular equation of curve

Find the rectangular equation of the $r o s e r = 4 \sin 2 θ .$ $r o s e r = 4 \sin 2 θ .$

Using the trigonometric identity $\sin 2 θ = 2 \sin θ \cos θ$ $\sin 2 θ = 2 \sin θ \cos θ$ and Eqs. (21.41) and (21.42) leads to the solution:

\begin{array}{rcl} r & = & 4 \sin 2 θ & polar equation \\ = & 4 (2 \sin θ \cos θ) = 8 \sin θ \cos θ & using identity \\ \sqrt{x^{2} + y^{2}} & = & 8 (\frac{y}{r}) (\frac{x}{r}) = \frac{8 x y}{r^{2}} = \frac{8 x y}{x^{2} + y^{2}} & using Eqs . (21.41) and (21.42) \\ x^{2} + y^{2} & = & \frac{64 x^{2} y^{2}}{{(x^{2} + y^{2})}^{2}} & squaring both sides \\ {(x^{2} + y^{2})}^{3} & = & 64 x^{2} y^{2} & simplifying \end{array}

$\begin{array}{rcl} r & = & 4 \sin 2 θ & polar equation \\ = & 4 (2 \sin θ \cos θ) = 8 \sin θ \cos θ & using identity \\ \sqrt{x^{2} + y^{2}} & = & 8 (\frac{y}{r}) (\frac{x}{r}) = \frac{8 x y}{r^{2}} = \frac{8 x y}{x^{2} + y^{2}} & using Eqs . (21.41) and (21.42) \\ x^{2} + y^{2} & = & \frac{64 x^{2} y^{2}}{{(x^{2} + y^{2})}^{2}} & squaring both sides \\ {(x^{2} + y^{2})}^{3} & = & 64 x^{2} y^{2} & simplifying \end{array}$

Plotting the graph of this equation from the rectangular equation would be complicated. However, as we will see in the next section, plotting this graph in polar coordinates is quite simple. The curve is shown in Fig. 21.111.

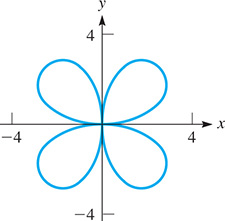
The graph is a 4 petal curve centered at (0, 0). A petal or loop extends into each quadrant. — Fig. 21.111

Exercises 21.10

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the indicated problems.

For both of the points plotted in Example 2, change $2 π / 3$ $2 π / 3$ to $π / 3$ $π / 3$ and then find another set of coordinates for each point, similar to those shown for the points in the example.
In Example 4, change $π / 4$ $π / 4$ to $π / 6$ $π / 6$
In Example 5, change 3 to $- 3$ $- 3$ and $- 5$ $- 5$ to 5.
In Example 7, change sin to cos.

In Exercises 5–16, plot the given polar coordinate points on polar coordinate paper.

$(3, \frac{π}{6})$ $(3, \frac{π}{6})$
$(2, π)$ $(2, π)$
$(\frac{5}{2}, - \frac{2 π}{5})$ $(\frac{5}{2}, - \frac{2 π}{5})$
$(5, - \frac{π}{3})$ $(5, - \frac{π}{3})$
$(- 8, \frac{7 π}{6})$ $(- 8, \frac{7 π}{6})$
$(- 5, \frac{π}{4})$ $(- 5, \frac{π}{4})$
$(- 3, - \frac{5 π}{4})$ $(- 3, - \frac{5 π}{4})$
$(- 4, - \frac{5 π}{3})$ $(- 4, - \frac{5 π}{3})$
(2, 2)
$(- 6, - 6)$ $(- 6, - 6)$
$(0.5, - 8.4)$ $(0.5, - 8.4)$
$(- 2.2, 18.8)$ $(- 2.2, 18.8)$

In Exercises 17–22, find a set of polar coordinates for each of the points for which the rectangular coordinates are given.

$(\sqrt{3}, 1)$ $(\sqrt{3}, 1)$
$(- 3, 3)$ $(- 3, 3)$
$(- \frac{\sqrt{3}}{2}, - \frac{1}{2})$ $(- \frac{\sqrt{3}}{2}, - \frac{1}{2})$
$(- 10, 8)$ $(- 10, 8)$
(0, 4)
$(- 5, 0)$ $(- 5, 0)$

In Exercises 23–28, find the rectangular coordinates for each of the points for which the polar coordinates are given.

$(8, \frac{4 π}{3})$ $(8, \frac{4 π}{3})$
$(4, - π)$ $(4, - π)$
$(- 3.0, - 0.40)$ $(- 3.0, - 0.40)$
$(- 3.0, 3.0)$ $(- 3.0, 3.0)$
$(8.0, - 8.0)$ $(8.0, - 8.0)$
$(π, 4.0)$ $(π, 4.0)$

In Exercises 29–38, find the polar equation of each of the given rectangular equations.

$x = 3$ $x = 3$
$y = - x$ $y = - x$
$x + 2 y + 3 = 0$ $x + 2 y + 3 = 0$
$x^{2} + y^{2} = 0.81$ $x^{2} + y^{2} = 0.81$
$x^{2} + {(y - 2)}^{2} = 4$ $x^{2} + {(y - 2)}^{2} = 4$
$x^{2} - y^{2} = 0.01$ $x^{2} - y^{2} = 0.01$
$x^{2} + 4 y^{2} = 4$ $x^{2} + 4 y^{2} = 4$
$y^{2} = 4 x$ $y^{2} = 4 x$
$x^{2} + y^{2} = 6 y$ $x^{2} + y^{2} = 6 y$
$x y = 9$ $x y = 9$

In Exercises 39–48, find the rectangular equation of each of the given polar equations. In Exercises 39–46, identify the curve that is represented by the equation.

$r = \sin θ$ $r = \sin θ$
$r sec θ = 4$ $r sec θ = 4$
$r \cos θ = 4$ $r \cos θ = 4$
$r = - 2 \csc θ$ $r = - 2 \csc θ$
$r = \frac{2}{\cos θ - 3 \sin θ}$ $r = \frac{2}{\cos θ - 3 \sin θ}$
$r = e^{r \cos θ} \csc θ$ $r = e^{r \cos θ} \csc θ$
$r = 4 \cos θ + 2 \sin θ$ $r = 4 \cos θ + 2 \sin θ$
$r \sin (θ + π / 6) = 3$ $r \sin (θ + π / 6) = 3$
$r^{2} = \sin 2 θ$ $r^{2} = \sin 2 θ$
$r = \frac{3}{\sin θ + 4 \cos θ}$ $r = \frac{3}{\sin θ + 4 \cos θ}$

In Exercises 49–60, solve the given problems. All coordinates given are polar coordinates.

Is the point $(2, 3 π / 4)$ $(2, 3 π / 4)$ on the curve $r = 2 \sin 2 θ ?$ $r = 2 \sin 2 θ ?$
Is the point $(1/2, 3 π / 2)$ $(1/2, 3 π / 2)$ on the curve $r = \sin (θ / 3) ?$ $r = \sin (θ / 3) ?$
Show that the polar coordinate equation $r = a \sin θ + b \cos θ$ $r = a \sin θ + b \cos θ$ represents a circle by changing it to a rectangular equation.
Find the distance between the points $(3, π / 6)$ $(3, π / 6)$ and $(4, π / 2)$ $(4, π / 2)$ by using the law of cosines.
The center of a regular hexagon is at the pole with one vertex at $(2, π) .$ $(2, π) .$ What are the polar coordinates of the other vertices?
Find the distance between the points $(4, π / 6)$ $(4, π / 6)$ and $(5, 5 π / 3) .$ $(5, 5 π / 3) .$
Under certain conditions, the x- and y-components of a magnetic field B are given by the equations

$B_{x} = \frac{- k y}{x^{2} + y^{2}} and B_{y} = \frac{k x}{x^{2} + y^{2}}$ $B_{x} = \frac{- k y}{x^{2} + y^{2}} and B_{y} = \frac{k x}{x^{2} + y^{2}}$

Write these equations in terms of polar coordinates.
In designing a domed roof for a building, an architect uses the equation $x^{2} + \frac{y^{2}}{k^{2}} = 1,$ $x^{2} + \frac{y^{2}}{k^{2}} = 1,$ where k is a constant. Write this equation in polar form.
The shape of a swimming pool can be described by the polar equation $r = 5 \cos θ$ $r = 5 \cos θ$ (dimensions in meters). Find the rectangular equation for the perimeter of the pool.
The polar equation of the path of a weather satellite of Earth is $r = \frac{4800}{1 + 0.14 \cos θ},$ $r = \frac{4800}{1 + 0.14 \cos θ},$ where r is measured in miles. Find the rectangular equation of the path of this satellite. The path is an ellipse, with Earth at one of the foci.
The control tower of an airport is taken to be at the pole, and the polar axis is taken as due east in a polar coordinate graph. How far apart (in km) are planes, at the same altitude, if their positions on the graph are (6.10, 1.25) and (8.45, 3.74)?
The perimeter of a certain type of machine part can be described by the equation $r = a \sin θ + b \cos θ (a > 0, b > 0) .$ $r = a \sin θ + b \cos θ (a > 0, b > 0) .$ Explain why all such machine parts are circular.

Answers to Practice Exercises

$(- 2 \sqrt{3}, 2)$ $(- 2 \sqrt{3}, 2)$
$r = - 2 \cos θ$ $r = - 2 \cos θ$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 21.10 Polar Coordinates

Create new playlist

Sign In

Sign Up

Table of Contents for
21.10 Polar Coordinates