Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

20.1 Fundamental Trigonometric Identities

Trigonometric Identities • Basic Identities • Proving Trigonometric Identities

From the definitions in Chapters 4 and 8, recall that $\sin θ = y / r$ $\sin θ = y / r$ and $\csc θ = r / y$ $\csc θ = r / y$ (see Fig. 20.1). Because $y / r = 1 / (r / y),$ $y / r = 1 / (r / y),$ we see that $\sin θ = 1 / \csc θ .$ $\sin θ = 1 / \csc θ .$ These definitions hold for any angle, which means that $\sin θ = 1 / \csc θ$ $\sin θ = 1 / \csc θ$ is true for any angle. This type of relation, which is true for any value of the variable, is called an identity. Of course, values where division by zero would be indicated are excluded.

A ray of length r rises from (0, 0) and through (x, y) at angle theta to the x-axis. Dashed segment y falls from (x, y) and meets the x-axis at a right angle. From here back to the origin is x. — Fig. 20.1

In this section, we develop several important identities involving the trigonometric functions. We also show how the basic identities are used to verify other identities.

From the definitions, we have

\begin{array}{l} \begin{array}{l} \sin θ \csc θ = \frac{y}{r} \times \frac{r}{y} = 1 or \sin θ = \frac{1}{\csc θ} or \csc θ = \frac{1}{\sin θ} \\ \cos θ \sec θ = \frac{x}{r} \times \frac{r}{x} = 1 or \cos θ = \frac{1}{\sec θ} or \sec θ = \frac{1}{\cos θ} \\ \tan θ \cot θ = \frac{y}{x} \times \frac{x}{y} = 1 or \tan θ = \frac{1}{\cot θ} or \cot θ = \frac{1}{\tan θ} \end{array} \\ \frac{\sin θ}{\cos θ} = \frac{y / r}{x / r} = \frac{y}{x} = \tan θ \frac{\cos θ}{\sin θ} = \frac{x / r}{y / r} = \frac{x}{y} = \cot θ \end{array}

$\begin{array}{l} \begin{array}{l} \sin θ \csc θ = \frac{y}{r} \times \frac{r}{y} = 1 or \sin θ = \frac{1}{\csc θ} or \csc θ = \frac{1}{\sin θ} \\ \cos θ \sec θ = \frac{x}{r} \times \frac{r}{x} = 1 or \cos θ = \frac{1}{\sec θ} or \sec θ = \frac{1}{\cos θ} \\ \tan θ \cot θ = \frac{y}{x} \times \frac{x}{y} = 1 or \tan θ = \frac{1}{\cot θ} or \cot θ = \frac{1}{\tan θ} \end{array} \\ \frac{\sin θ}{\cos θ} = \frac{y / r}{x / r} = \frac{y}{x} = \tan θ \frac{\cos θ}{\sin θ} = \frac{x / r}{y / r} = \frac{x}{y} = \cot θ \end{array}$

Also, from the definitions and the Pythagorean theorem in the form of $x^{2} + y^{2} = r^{2},$ $x^{2} + y^{2} = r^{2},$ we arrive at the following identities.

By dividing the Pythagorean relation through by $r^{2},$ $r^{2},$ we have

{(\frac{x}{r})}^{2} + {(\frac{y}{r})}^{2} = 1 which leads us to \cos^{2} θ + \sin^{2} θ = 1

${(\frac{x}{r})}^{2} + {(\frac{y}{r})}^{2} = 1 which leads us to \cos^{2} θ + \sin^{2} θ = 1$

By dividing the Pythagorean relation by $x^{2},$ $x^{2},$ we have

1 + {(\frac{y}{x})}^{2} = {(\frac{r}{x})}^{2} which leads us to 1 + \tan^{2} θ = \sec^{2} θ

$1 + {(\frac{y}{x})}^{2} = {(\frac{r}{x})}^{2} which leads us to 1 + \tan^{2} θ = \sec^{2} θ$

By dividing the Pythagorean relation by $y^{2},$ $y^{2},$ we have

{(\frac{x}{y})}^{2} + 1 = {(\frac{r}{y})}^{2} which leads us to \cot^{2} θ + 1 = \csc^{2} θ

${(\frac{x}{y})}^{2} + 1 = {(\frac{r}{y})}^{2} which leads us to \cot^{2} θ + 1 = \csc^{2} θ$

BASIC IDENTITIES

NOTE

[The term $\cos^{2} θ$ $\cos^{2} θ$ is the common way of writing ${(\cos θ)}^{2},$ ${(\cos θ)}^{2},$ and it means to square the value of the cosine of the angle.]

Obviously, the same holds true for the other functions.

Summarizing these results, we have the following important identities.

\sin θ = \frac{1}{\csc θ}

$\sin θ = \frac{1}{\csc θ}$ (20.1)

\cos θ = \frac{1}{\sec θ}

$\cos θ = \frac{1}{\sec θ}$ (20.2)

\tan θ = \frac{1}{\cot θ}

$\tan θ = \frac{1}{\cot θ}$ (20.3)

\tan θ = \frac{\sin θ}{\cos θ}

$\tan θ = \frac{\sin θ}{\cos θ}$ (20.4)

\cot θ = \frac{\cos θ}{\sin θ}

$\cot θ = \frac{\cos θ}{\sin θ}$ (20.5)

\sin^{2} θ + \cos^{2} θ = 1

$\sin^{2} θ + \cos^{2} θ = 1$ (20.6)

1 + \tan^{2} θ = \sec^{2} θ

$1 + \tan^{2} θ = \sec^{2} θ$ (20.7)

1 + \cot^{2} θ = \csc^{2} θ

$1 + \cot^{2} θ = \csc^{2} θ$ (20.8)

In using the basic identities, $θ$ $θ$ may stand for any angle or number or expression representing an angle or a number.

EXAMPLE 1 Using basic identities

$\sin a x = \frac{1}{\csc a x} using Eq . (20.1)$ $\sin a x = \frac{1}{\csc a x} using Eq . (20.1)$
$\tan 157 ° = \frac{\sin 157 °}{\cos 157 °} using Eq . (20.4)$ $\tan 157 ° = \frac{\sin 157 °}{\cos 157 °} using Eq . (20.4)$
$\sin^{2} \frac{π}{4} + \cos^{2} \frac{π}{4} = 1 using Eq . (20.6)$ $\sin^{2} \frac{π}{4} + \cos^{2} \frac{π}{4} = 1 using Eq . (20.6)$

EXAMPLE 2 Checking identities with numerical values

Let us check the last two illustrations of Example 1 for the given values of $θ .$ $θ .$

Using a calculator, we find that

$\frac{\sin 157 °}{\cos 157 °} = \frac{0.3907311285}{- 0.9205048535} = - 0.4244748162 and \tan 157 ° = - 0.4244748162$ $\frac{\sin 157 °}{\cos 157 °} = \frac{0.3907311285}{- 0.9205048535} = - 0.4244748162 and \tan 157 ° = - 0.4244748162$

We see that $\sin 157 ° / \cos 157 ° = \tan 157 ° .$ $\sin 157 ° / \cos 157 ° = \tan 157 ° .$
Checking Example 1(c), refer to Fig. 20.2.

Fig. 20.2

Figure 20.2 Full Alternative Text

$\begin{array}{l} \sin \frac{π}{4} = \sin 45 ° = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} and \cos \frac{π}{4} = \cos 45 ° = \frac{\sqrt{2}}{2} \\ \sin^{2} \frac{π}{4} + \cos^{2} \frac{π}{4} = {(\frac{\sqrt{2}}{2})}^{2} + {(\frac{\sqrt{2}}{2})}^{2} = \frac{1}{2} + \frac{1}{2} = 1 \end{array}$ $\begin{array}{l} \sin \frac{π}{4} = \sin 45 ° = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} and \cos \frac{π}{4} = \cos 45 ° = \frac{\sqrt{2}}{2} \\ \sin^{2} \frac{π}{4} + \cos^{2} \frac{π}{4} = {(\frac{\sqrt{2}}{2})}^{2} + {(\frac{\sqrt{2}}{2})}^{2} = \frac{1}{2} + \frac{1}{2} = 1 \end{array}$

We see that this checks with Eq. (20.6) for these values.

EXAMPLE 3 Simplifying basic expressions

Multiply and simplify the expression $\sin θ \tan θ (\csc θ + \cot θ) .$ $\sin θ \tan θ (\csc θ + \cot θ) .$

$\begin{array}{r} \begin{array}{rcl} \sin θ \tan θ (\csc θ + \cot θ) & = & \sin θ \tan θ \csc θ + \sin θ \tan θ \cot θ \\ = & (\frac{1}{\csc θ}) \tan θ \csc θ + \sin θ (\frac{1}{\cot θ}) \cot θ \\ = & \tan θ + \sin θ \end{array} & \begin{array}{l} using Eqs . \\ (20.1) and \\ (20.4) \end{array} \end{array}$ $\begin{array}{r} \begin{array}{rcl} \sin θ \tan θ (\csc θ + \cot θ) & = & \sin θ \tan θ \csc θ + \sin θ \tan θ \cot θ \\ = & (\frac{1}{\csc θ}) \tan θ \csc θ + \sin θ (\frac{1}{\cot θ}) \cot θ \\ = & \tan θ + \sin θ \end{array} & \begin{array}{l} using Eqs . \\ (20.1) and \\ (20.4) \end{array} \end{array}$
Factor and simplify the expression $\tan^{3} α + \tan α .$ $\tan^{3} α + \tan α .$

$\begin{array}{rcll} \tan^{3} α + \tan α & = & \tan α (\tan^{2} α + 1) \\ = & \tan α \sec^{2} α & using Eq . (20.7) \end{array}$ $\begin{array}{rcll} \tan^{3} α + \tan α & = & \tan α (\tan^{2} α + 1) \\ = & \tan α \sec^{2} α & using Eq . (20.7) \end{array}$

We see that when algebraic operations are performed on trigonometric terms, they are handled in just the same way as with algebraic terms. This is true for the basic operations of addition, subtraction, multiplication, and division, as well as other operations used in simplifying expressions, such as factoring or taking roots.

PROVING TRIGONOMETRIC IDENTITIES

A great many identities exist among the trigonometric functions. We are going to use the basic identities that have been developed in Eqs. (20.1) through (20.8), along with a few additional ones developed in later sections to prove the validity of still other identities.

CAUTION

The ability to prove trigonometric identities depends to a large extent on being very familiar with the basic identities so that you can recognize them in somewhat different forms.

If you do not learn these basic identities and learn them well, you will have difficulty in following the examples and doing the exercises. The more readily you recognize these forms, the more easily you will be able to prove such identities.

In proving identities, look for combinations that appear in, or are very similar to, those in the basic identities. This is illustrated in the following examples.

EXAMPLE 4 Proving a trig identity

In proving the identity

\sin x = \frac{\cos x}{\cot x}

$\sin x = \frac{\cos x}{\cot x}$

we know that $\cot x = \frac{\cos x}{\sin x} .$ $\cot x = \frac{\cos x}{\sin x} .$ Because sin x appears on the left, substituting for cot x on the right will eliminate cot x and introduce sin x. This should help us proceed in proving the identity. Thus, starting with the right-hand side, we have

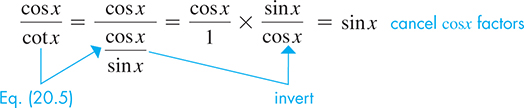
An equation where cosine of x factors are canceled.

.1-2 Full Alternative Text

By showing that the right side may be changed exactly to sin x, the expression on the left side, we have proved the identity.

Some important points should be made in relation to the proof of the identity of Example 4. We must recognize which basic identities may be useful. The proof of an identity requires the use of the basic algebraic operations, and these must be done carefully and correctly. Although in Example 4, we changed the right side to the form on the left, we could have changed the left to the form on the right. From this and the fact that various substitutions are possible, we see that a variety of procedures can be used to prove any given identity.

CAUTION

Performing the algebraic operations carefully and correctly is very important when working with trigonometric expressions. Operations such as substituting, factoring, and simplifying fractions are frequently used.

EXAMPLE 5 Trig identity—two different solutions

Prove that $\tan θ \csc θ = \sec θ .$ $\tan θ \csc θ = \sec θ .$

In proving this identity, we know that $\tan θ = \frac{\sin θ}{\cos θ}$ $\tan θ = \frac{\sin θ}{\cos θ}$ and also that $\frac{1}{\cos θ} = \sec θ .$ $\frac{1}{\cos θ} = \sec θ .$ Thus, by substituting for $\tan θ,$ $\tan θ,$ we introduce $\cos θ$ $\cos θ$ in the denominator, which is equivalent to introducing $\sec θ$ $\sec θ$ in the numerator. Therefore, changing only the left side, we have

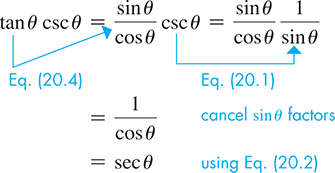
An illustration of a trigonometric function.

.1-3 Full Alternative Text

Having changed the left side into the form on the right side, we have proven the identity.

Many variations of the preceding steps are possible. We could have changed the right side to obtain the form on the left. For example,

\begin{array}{rcl} \sec θ & = & \frac{1}{\cos θ} & using Eq . (20.2) \\ = & \frac{\sin θ}{\cos θ \sin θ} = \frac{\sin θ}{\cos θ} \frac{1}{\sin θ} & \begin{array}{l} multiply numerator and \\ denominator by \sin θ and rewrite \end{array} \\ = & \tan θ \csc θ & using Eqs . (20.4) and (20.1) \end{array}

$\begin{array}{rcl} \sec θ & = & \frac{1}{\cos θ} & using Eq . (20.2) \\ = & \frac{\sin θ}{\cos θ \sin θ} = \frac{\sin θ}{\cos θ} \frac{1}{\sin θ} & \begin{array}{l} multiply numerator and \\ denominator by \sin θ and rewrite \end{array} \\ = & \tan θ \csc θ & using Eqs . (20.4) and (20.1) \end{array}$

In proving the identities in Examples 4 and 5, we showed that the expression on one side of the equal sign can be changed into the expression on the other side. Because we want to prove that the expressions are equal, we cannot transpose terms or multiply each side by the same quantity as we do when solving equations. Each side must be treated separately. In this way, we know the form we are attempting to attain, and by looking ahead, we are better able to make the necessary changes.

NOTE

[Although we could make changes to each side independently to hopefully arrive at the same expression, we will restrict the method of proof to changing only one side into the same form as the other side.]

There is no set procedure for working with identities. The most important factors are to (1) recognize the proper forms, (2) try to identify what effect a change may have before performing it, and (3) perform all steps correctly. If the forms are about the same, a first close look often suggests possible steps to use.

NOTE

[Normally, it is easier to change the form of the more complicated side to the same form as the less complicated side.]

EXAMPLE 6 Proving a trig identity

Prove the identity $\frac{\sec^{2} y}{\cot y} - \tan^{3} y = \tan y .$ $\frac{\sec^{2} y}{\cot y} - \tan^{3} y = \tan y .$

Because the more complicated side is on the left, we will change the left side to tan y, the form on the right. Because we want tan y as the final form, we will use the basic identities to introduce tan y where possible. Thus, noting the cot y in the denominator, we substitute 1/tan y for cot y. This gives

Solving, start fraction, secant squared y over cotangent y, end fraction minus tangent cube y.

.1-4 Full Alternative Text

In the form on the right we now note the factor of tan y in each term. Factoring tan y from each of these terms, and then using the basic identity $1 + \tan^{2} y = \sec^{2} y$ $1 + \tan^{2} y = \sec^{2} y$ in the form $\sec^{2} y - \tan^{2} y = 1,$ $\sec^{2} y - \tan^{2} y = 1,$ we can complete the proof. Therefore,

Trigonometric function. secant square y times tangent y minus tangent cube y = tangent y times secant square y minus tangent square y = tangent y times 1, secant square y minus tangent square y refers to 1 = tangent y.

NOTE

[Note carefully that we had to use the identity $1 + \tan^{2} y = \sec^{2} y$ $1 + \tan^{2} y = \sec^{2} y$ in a somewhat different form from that shown in Eq. (20.7).]

The use of such variations in form to prove identities is a very common procedure.

EXAMPLE 7 Proving a trig identity

Prove the identity $\frac{1 - \sin x}{\sin x \cot x} = \frac{\cos x}{1 + \sin x} .$ $\frac{1 - \sin x}{\sin x \cot x} = \frac{\cos x}{1 + \sin x} .$

The combination $1 - \sin x$ $1 - \sin x$ also suggests $1 - \sin^{2} x,$ $1 - \sin^{2} x,$ since multiplying $(1 - \sin x)$ $(1 - \sin x)$ by $(1 + \sin x)$ $(1 + \sin x)$ gives $1 - \sin^{2} x,$ $1 - \sin^{2} x,$ which can then be replaced by $\cos^{2} x .$ $\cos^{2} x .$ Thus, changing only the left side, we have

.1-6 Full Alternative Text

EXAMPLE 8 Trig identity—radiation rate of electric charge

In finding the radiation rate of an accelerated electric charge, it is necessary to show that $\sin^{3} θ = \sin θ - \sin θ \cos^{2} θ .$ $\sin^{3} θ = \sin θ - \sin θ \cos^{2} θ .$ Show this by changing the left side.

Because each term on the right has a factor of $\sin θ,$ $\sin θ,$ we see that we can proceed by writing $\sin^{3} θ$ $\sin^{3} θ$ as $\sin θ (s i n^{2} θ) .$ $\sin θ (s i n^{2} θ) .$ Then the factor $\sin^{2} θ$ $\sin^{2} θ$ and the $\cos^{2} θ$ $\cos^{2} θ$ on the right suggest the use of Eq. (20.6). Thus, we have

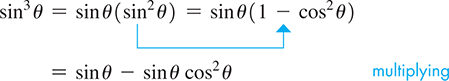
Sine cube theta = sine theta times sine square theta = sin theta times 1 minus cosine square theta, sine square theta refers to 1 minus cosine square theta. multiply to get = sine theta minus sine square theta times cosine square theta.

Because we substituted for $\sin^{2} θ,$ $\sin^{2} θ,$ we used Eq. (20.6) in the form $\sin^{2} θ^{} = 1 - \cos^{2} θ .$ $\sin^{2} θ^{} = 1 - \cos^{2} θ .$

EXAMPLE 9 Simplifying a trig expression

Simplify the expression $\frac{\csc x}{\tan x + \cot x} .$ $\frac{\csc x}{\tan x + \cot x} .$

We proceed with a simplification in a manner similar to proving an identity, although we do not know what the result should be. Following is one procedure for this simplification:

.1-8 Full Alternative Text

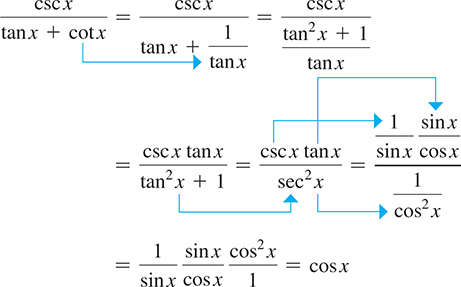
A calculator can be used to check an identity or a simplification. This is done by graphing the function on each side of an identity, or the initial expression and the final expression for simplification. If the two graphs are the same, the identity or simplification is probably shown to be correct, although this is not strictly a proof.

EXAMPLE 10 Trig identity—verifying by calculator

Use a calculator to verify the identity of Example 7.

Noting this identity as $\frac{1 - \sin x}{\sin x \cot x} = \frac{\cos x}{1 + \sin x},$ $\frac{1 - \sin x}{\sin x \cot x} = \frac{\cos x}{1 + \sin x},$ on a calculator, we let

\begin{array}{rcll} y_{1} & = & (1 - \sin x) / (\sin x / \tan x) & noting that \cot x = 1 \tan x \\ y_{2} & = & \cos x / (1 + \sin x) \end{array}

$\begin{array}{rcll} y_{1} & = & (1 - \sin x) / (\sin x / \tan x) & noting that \cot x = 1 \tan x \\ y_{2} & = & \cos x / (1 + \sin x) \end{array}$

We then graph these two functions as shown in Fig. 20.3. The screenshot shows $y_{2}$ $y_{2}$ (in red) in the process of being plotted right on top of $y_{1}$ $y_{1}$ (in blue). Because these curves are the same, the identity appears to be verified (although it has not been proven).

The graph is periodic about the x-axis. One cycle falls from an asymptote with decreasing steepness, inflects on the x-axis, then falls within increasing steepness. — Fig. 20.3

Working with trigonometric identities has often been considered a difficult topic. However, as we emphasized earlier, knowing the basic identities very well and performing the necessary algebraic steps properly should make proving these identities a much easier task.

EXERCISES 20.1

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then prove the resulting identities.

In Example 4, change the right side to tan x/sec x.
In Example 6, change the first term on the left to $\sin y / \cos^{3} y .$ $\sin y / \cos^{3} y .$

In Exercises 3–6, use a calculator to check the indicated basic identities for the given angles.

Eq. (20.4) for $θ = 38 °$ $θ = 38 °$
Eq. (20.5) for $θ = 280 °$ $θ = 280 °$
Eq. (20.6) for $θ = 4 π / 3$ $θ = 4 π / 3$
Eq. (20.7) for $θ = 5 π / 6$ $θ = 5 π / 6$

In Exercises 7–12, multiply and simplify. In Exercises 13–18, factor and simplify.

$\cos x (\tan x - \sec x)$ $\cos x (\tan x - \sec x)$
$\csc y (\sin y + 3 \cos y)$ $\csc y (\sin y + 3 \cos y)$
$\cos θ \cot θ (\sec θ - 2 \tan θ)$ $\cos θ \cot θ (\sec θ - 2 \tan θ)$
$(\csc x - 1) (\csc x + 1)$ $(\csc x - 1) (\csc x + 1)$
$\tan u (\cot u + \tan u)$ $\tan u (\cot u + \tan u)$
$\cos^{2} t (1 + \tan^{2} t)$ $\cos^{2} t (1 + \tan^{2} t)$
$\sin x + {\sin x \tan}^{2} x$ $\sin x + {\sin x \tan}^{2} x$
$\sin θ - \sin θ \cos^{2} θ$ $\sin θ - \sin θ \cos^{2} θ$
$\sin^{3} t \cos t + {\sin t \cos}^{3} t$ $\sin^{3} t \cos t + {\sin t \cos}^{3} t$
$\tan^{2} {u \sec}^{2} u - \tan^{4} u$ $\tan^{2} {u \sec}^{2} u - \tan^{4} u$
$\csc^{4} y - 1$ $\csc^{4} y - 1$
$\sin x + {\sin x \cot}^{2} x$ $\sin x + {\sin x \cot}^{2} x$

In Exercises 19–38, prove the given identities.

$\frac{\sin x}{\tan x} = \cos x$ $\frac{\sin x}{\tan x} = \cos x$
$\frac{\csc θ}{\sec θ} = \cot θ$ $\frac{\csc θ}{\sec θ} = \cot θ$
$\sin x \sec x = \tan x$ $\sin x \sec x = \tan x$
$\cot θ \sec θ = \csc θ$ $\cot θ \sec θ = \csc θ$
$\csc^{2} x (1 - \cos^{2} x) = 1$ $\csc^{2} x (1 - \cos^{2} x) = 1$
$\sec θ (1 - \sin^{2} θ) = \cos θ$ $\sec θ (1 - \sin^{2} θ) = \cos θ$
$\sin x (1 + \cot^{2} x) = \csc x$ $\sin x (1 + \cot^{2} x) = \csc x$
$\csc x (\csc x - \sin x) = \cot^{2} x$ $\csc x (\csc x - \sin x) = \cot^{2} x$
$\cos θ \cot θ + \sin θ = \csc θ$ $\cos θ \cot θ + \sin θ = \csc θ$
$\frac{\csc x}{\cos x} - \tan x = \cot x$ $\frac{\csc x}{\cos x} - \tan x = \cot x$
$\cot θ \sec^{2} θ - \frac{1}{\tan θ} = \tan θ$ $\cot θ \sec^{2} θ - \frac{1}{\tan θ} = \tan θ$
$\sin y + {\sin y \cot}^{2} y = \csc y$ $\sin y + {\sin y \cot}^{2} y = \csc y$
$\tan x + \cot x = \sec x \csc x$ $\tan x + \cot x = \sec x \csc x$
$\tan x + \cot x = {\tan x \csc}^{2} x$ $\tan x + \cot x = {\tan x \csc}^{2} x$
$\cos^{2} x - \sin^{2} x = 1 - 2 \sin^{2} x$ $\cos^{2} x - \sin^{2} x = 1 - 2 \sin^{2} x$
$\frac{1 + \cos x}{\sin x} = \frac{\sin x}{1 - \cos x}$ $\frac{1 + \cos x}{\sin x} = \frac{\sin x}{1 - \cos x}$
$\frac{\sin θ}{\csc θ} + \frac{\cos θ}{\sec θ} = 1$ $\frac{\sin θ}{\csc θ} + \frac{\cos θ}{\sec θ} = 1$
$\frac{\sec θ}{\cos θ} - \frac{\tan θ}{\cot θ} = 1$ $\frac{\sec θ}{\cos θ} - \frac{\tan θ}{\cot θ} = 1$
$2 \sin^{4} x - 3 \sin^{2} x + 1 = \cos^{2} x (1 - 2 \sin^{2} x)$ $2 \sin^{4} x - 3 \sin^{2} x + 1 = \cos^{2} x (1 - 2 \sin^{2} x)$
$\frac{\sin^{2} θ + 2 \cos θ - 1}{\sin^{2} θ + 3 \cos θ - 3} = \frac{1}{1 - \sec θ}$ $\frac{\sin^{2} θ + 2 \cos θ - 1}{\sin^{2} θ + 3 \cos θ - 3} = \frac{1}{1 - \sec θ}$

In Exercises 39–46, simplify the given expressions. The result will be one of sin x, cos x, tan x, cot x, sec x, or csc x.

$\frac{{\tan x \csc}^{2} x}{1 + \tan^{2} x}$ $\frac{{\tan x \csc}^{2} x}{1 + \tan^{2} x}$
$\frac{\cos x - \cos^{3} x}{\sin x - \sin^{3} x}$ $\frac{\cos x - \cos^{3} x}{\sin x - \sin^{3} x}$
$\cot x (\sec x - \cos x)$ $\cot x (\sec x - \cos x)$
$\sin x (\tan x + \cot x)$ $\sin x (\tan x + \cot x)$
$\frac{\tan x + \cot x}{\csc x}$ $\frac{\tan x + \cot x}{\csc x}$
$\frac{1 + \tan x}{\sin x} - \sec x$ $\frac{1 + \tan x}{\sin x} - \sec x$
$\frac{\cos x + \sin x}{1 + \tan x}$ $\frac{\cos x + \sin x}{1 + \tan x}$
$\frac{\sec x - \cos x}{\tan x}$ $\frac{\sec x - \cos x}{\tan x}$

In Exercises 47–50, for a first-quadrant angle, express the first function listed in terms of the second function listed.

sin x, sec x
cos x, csc x
tan x, csc x
cot x, sec x

In Exercises 51–54, use a calculator to verify the given identities by comparing the graphs of each side.

$\sin x (\csc x - \sin x) = \cos^{2} x$ $\sin x (\csc x - \sin x) = \cos^{2} x$
$\cos y (\sec y - \cos y) = \sin^{2} y$ $\cos y (\sec y - \cos y) = \sin^{2} y$
$\frac{\sec x + \csc x}{1 + \tan x} = \csc x$ $\frac{\sec x + \csc x}{1 + \tan x} = \csc x$
$\frac{\cot x + 1}{\cot x} = 1 + \tan x$ $\frac{\cot x + 1}{\cot x} = 1 + \tan x$

In Exercises 55–58, use a calculator to determine whether the given equations are identities.

$\sec θ \tan θ \csc θ = \tan^{2} θ + 1$ $\sec θ \tan θ \csc θ = \tan^{2} θ + 1$
$\sin x \cos x \tan x = \cos^{2} x - 1$ $\sin x \cos x \tan x = \cos^{2} x - 1$
$\frac{2 \cos^{2} x - 1}{\sin x \cos x} = \tan x - \cot x$ $\frac{2 \cos^{2} x - 1}{\sin x \cos x} = \tan x - \cot x$
$\cos^{3} {x \csc}^{3} {x \tan}^{3} x = \csc^{2} x - \cot^{2} x$ $\cos^{3} {x \csc}^{3} {x \tan}^{3} x = \csc^{2} x - \cot^{2} x$

In Exercises 59–62, solve the given problems involving trigonometric identities.

When designing a solar-energy collector, it is necessary to account for the latitude and longitude of the location, the angle of the sun, and the angle of the collector. In doing this, the equation $\cos θ = \cos A \cos B \cos C + \sin A \sin B$ $\cos θ = \cos A \cos B \cos C + \sin A \sin B$ is used. If $θ = 90 °,$ $θ = 90 °,$ show that $\cos C = - \tan A \tan B .$ $\cos C = - \tan A \tan B .$
In determining the path of least time between two points under certain conditions, it is necessary to show that

$\sqrt{\frac{1 + \cos θ}{1 - \cos θ}} \sin θ = 1 + \cos θ$ $\sqrt{\frac{1 + \cos θ}{1 - \cos θ}} \sin θ = 1 + \cos θ$

Show this by transforming the left-hand side.
Show that the length l of the straight brace shown in Fig. 20.4 can be found from the equation

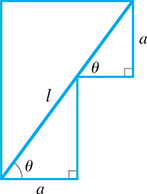
Fig. 20.4

Figure 20.4 Full Alternative Text

$l = \frac{a (1 + \tan θ)}{\sin θ}$ $l = \frac{a (1 + \tan θ)}{\sin θ}$
The path of a point on the circumference of a circle, such as a point on the rim of a bicycle wheel as it rolls along, tracks out a curve called a cycloid. See Fig. 20.5. To find the distance through which a point moves, it is necessary to simplify the expression ${(1 - \cos θ)}^{2} + \sin^{2} θ .$ ${(1 - \cos θ)}^{2} + \sin^{2} θ .$ Perform this simplification.

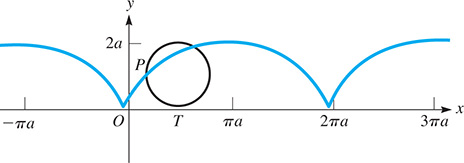
Fig. 20.5

Figure 20.5 Full Alternative Text

In Exercises 63–70, solve the given problems.

Explain how to transform $\sin θ \tan θ + \cos θ$ $\sin θ \tan θ + \cos θ$ into $\sec θ .$ $\sec θ .$
Explain how to transform $\tan^{2} θ \cos^{2} θ + \cot^{2} θ \sin^{2} θ$ $\tan^{2} θ \cos^{2} θ + \cot^{2} θ \sin^{2} θ$ into 1.
Show that $\sin^{2} x (1 - \sec^{2} x) + \cos^{2} x (1 + \sec^{4} x)$ $\sin^{2} x (1 - \sec^{2} x) + \cos^{2} x (1 + \sec^{4} x)$ has a constant value.
Show that cot y csc y sec $y - \csc y$ $y - \csc y$ cos y cot y has a constant value.
If $\tan x + \cot x = 2,$ $\tan x + \cot x = 2,$ evaluate $\tan^{2} x + \cot^{2} x .$ $\tan^{2} x + \cot^{2} x .$
If $\sec x + \cos x = 2,$ $\sec x + \cos x = 2,$ evaluate $\sec^{2} x + \cos^{2} x .$ $\sec^{2} x + \cos^{2} x .$
Prove that $\sec^{2} θ + \csc^{2} θ = \sec^{2} θ \csc^{2} θ$ $\sec^{2} θ + \csc^{2} θ = \sec^{2} θ \csc^{2} θ$ by expressing each function in terms of its x, y, and r definition.
Prove that $\frac{\csc θ}{\tan θ + \cot θ} = \cos θ$ $\frac{\csc θ}{\tan θ + \cot θ} = \cos θ$ by expressing each function in terms of its x, y, and r definition.

In Exercises 71–74, use the given substitutions to show that the given equations are valid. In each, $0 < θ < π / 2 .$ $0 < θ < π / 2 .$

If $x = \cos θ,$ $x = \cos θ,$ show that $\sqrt{1 - x^{2}} = \sin θ .$ $\sqrt{1 - x^{2}} = \sin θ .$
If $x = 3 \sin θ,$ $x = 3 \sin θ,$ show that $\sqrt{9 - x^{2}} = 3 \cos θ .$ $\sqrt{9 - x^{2}} = 3 \cos θ .$
If $x = 2 \tan θ,$ $x = 2 \tan θ,$ show that $\sqrt{4 + x^{2}} = 2 \sec θ .$ $\sqrt{4 + x^{2}} = 2 \sec θ .$
If $x = 4 \sec θ,$ $x = 4 \sec θ,$ show that $\sqrt{x^{2} - 16} = 4 \tan θ .$ $\sqrt{x^{2} - 16} = 4 \tan θ .$

Answers to Practice Exercises

$1 + \sin x$ $1 + \sin x$
tan x
$\cot x (\cos^{2} x + \sin^{2} x) = \cot x$ $\cot x (\cos^{2} x + \sin^{2} x) = \cot x$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 20.1 Fundamental Trigonometric Identities

Create new playlist

Sign In

Sign Up

Table of Contents for
20.1 Fundamental Trigonometric Identities