Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

17.1 Properties of Inequalities

Solution of an Inequality • Conditional Inequality • Absolute Inequality • Properties of Inequalities

In Chapter 1, we first introduced the signs of inequality. To this point, only a basic understanding of their meanings has been necessary to show certain intervals associated with a variable. In this section, we review the meanings and develop certain basic properties of inequalities. We also show the meaning of the solution of an inequality and how it is shown on the number line.

The expression $a < b$ $a < b$ is read as “a is less than b,” and the expression $a > b$ $a > b$ is read as “a is greater than b.” These signs define what is known as the sense (indicated by the direction of the sign) of the inequality. Two inequalities are said to have the same sense if the signs of inequality point in the same direction. They are said to have the opposite sense if the signs of inequality point in opposite directions. The two sides of the inequality are called members of the inequality.

EXAMPLE 1 Sense of inequality

The inequalities $x + 3 > 2$ $x + 3 > 2$ and $x + 1 > 0$ $x + 1 > 0$ have the same sense, as do the inequalities $3 x - 1 < 4$ $3 x - 1 < 4$ and $x^{2} - 1 < 3.$ $x^{2} - 1 < 3.$

The inequalities $x - 4 < 0$ $x - 4 < 0$ and $x > - 4$ $x > - 4$ have the opposite sense, as do the inequalities $2 x + 4 > 1$ $2 x + 4 > 1$ and $3 x^{2} - 7 < 1.$ $3 x^{2} - 7 < 1.$

The solution of an inequality consists of all values of the variable that make the inequality a true statement. Most inequalities with which we deal are conditional inequalities, which are true for some, but not all, values of the variable. Also, some inequalities are true for all values of the variable, and they are called absolute inequalities. A solution of an inequality consists of only real numbers, as the terms greater than or less than have not been defined for complex numbers.

EXAMPLE 2 Conditional and absolute inequalities

The inequality $x + 1 > 0$ $x + 1 > 0$ is true for all values of x greater than $- 1.$ $- 1.$ Therefore, the values of x that satisfy this inequality are written as $x > - 1.$ $x > - 1.$ This illustrates the difference between the solution of an equation and the solution of an inequality. Any and all values within this interval are termed solutions of the inequality. Because the inequality $x + 1 > 0$ $x + 1 > 0$ is satisfied only by the values of x in the interval $x > - 1,$ $x > - 1,$ it is a conditional inequality.

NOTE

[The solution of an equation normally consists of a few specific numbers, whereas the solution to an inequality normally consists of an interval of values of the variable.]

The inequality $x^{2} + 1 > 0$ $x^{2} + 1 > 0$ is true for all real values of x, since $x^{2}$ $x^{2}$ is never negative. Therefore, it is an absolute inequality.

There are occasions when it is convenient to combine an inequality with an equality. For such purposes, the symbols $\leq,$ $\leq,$ meaning less than or equal to, and $\geq,$ $\geq,$ meaning greater than or equal to, are used.

EXAMPLE 3 Greater (or less) than or equal to

If we wish to state that x is positive, we can write $x > 0.$ $x > 0.$ However, the value zero is not included in the solution. If we wish to state that x is not negative, we write $x \geq 0.$ $x \geq 0.$ Here, zero is part of the solution.

In order to state that x is less than or equal to $- 5,$ $- 5,$ we write $x \leq - 5.$ $x \leq - 5.$

In the sections that follow, we will solve inequalities. It is often useful to show the solution on the number line. The next example shows how this is done.

EXAMPLE 4 Graphing solutions of inequalities

To graph $x > 2,$ $x > 2,$ we draw a small open circle at 2 on the number line (which is equivalent to the x-axis). Then we draw a solid line to the right of the point and with an arrowhead pointing to the right, indicating all values greater than 2. See Fig. 17.1(a). The open circle shows that the point is not part of the indicated solution.
To graph $x \leq 1,$ $x \leq 1,$ we follow the same basic procedure as in part (a), except that we use a solid circle and the arrowhead points to the left. See Fig. 17.1(b). The solid circle shows that the point is part of the indicated solution.

Figure 17.1 Full Alternative Text

PROPERTIES OF INEQUALITIES

We now show the basic operations performed on inequalities. These are the same operations as those performed on equations, but in certain cases the results take on a different form. The following are the properties of inequalities.

The sense of an inequality is not changed when the same number is added to—or subtracted from—both members of the inequality. Symbolically, this may be stated as “if $a > b,$ $a > b,$ then $a + c > b + c$ $a + c > b + c$ and $a - c > b - c .$ $a - c > b - c .$ ”

EXAMPLE 5 Illustrations of property 1

Using property 1 on the inequality $9 > 6,$ $9 > 6,$ we have the following results:

\begin{array}{c} 9 > 6 & 9 > 6 \\ add 4 to each member & subtract 12 from each member \\ 9 + 4 > 6 + 4 & 9 - 12 > 6 - 12 \\ 13 > 10 & - 3 > - 6 \end{array}

$\begin{array}{c} 9 > 6 & 9 > 6 \\ add 4 to each member & subtract 12 from each member \\ 9 + 4 > 6 + 4 & 9 - 12 > 6 - 12 \\ 13 > 10 & - 3 > - 6 \end{array}$

In Fig. 17.2, we see that 9 is to the right of 6, 13 is to the right of 10, and $- 3$ $- 3$ is to the right of $- 6.$ $- 6.$

A number line with closed circles at negative 6, negative 3, 6, 9, 10, and 13 from left to right. — Fig. 17.2

The sense of an inequality is not changed if both members are multiplied or divided by the same positive number. Symbolically, this is stated as “if $a > b,$ $a > b,$ then $a c > b c,$ $a c > b c,$ and $a / c > b / c,$ $a / c > b / c,$ provided that $c > 0.$ $c > 0.$ ”

EXAMPLE 6 Illustrations of property 2

Using property 2 on the inequality $8 < 15,$ $8 < 15,$ we have the following results:

\begin{array}{c} 8 < 15 & 8 < 15 \\ multiply both members by 2 & divide both members by 2 \\ 2 (8) < 2 (15) & \frac{8}{2} < \frac{15}{2} \\ 16 < 30 & 4 < \frac{15}{2} \end{array}

$\begin{array}{c} 8 < 15 & 8 < 15 \\ multiply both members by 2 & divide both members by 2 \\ 2 (8) < 2 (15) & \frac{8}{2} < \frac{15}{2} \\ 16 < 30 & 4 < \frac{15}{2} \end{array}$

The sense of an inequality is reversed if both members are multiplied or divided by the same negative number. Symbolically, this is stated as “if $a > b,$ $a > b,$ then $a c < b c,$ $a c < b c,$ and $a / c < b / c,$ $a / c < b / c,$ provided that $c < 0.$ $c < 0.$ ”

CAUTION

In using this property of inequalities, be very careful to note that the inequality sign remains the same if both members are multiplied or divided by a positive number, but that the inequality sign is reversed if both members are multiplied or divided by a negative number. Most of the errors made in dealing with inequalities occur when using this property.

EXAMPLE 7 Be careful in using property 3

Using property 3 on the inequality $4 > - 2,$ $4 > - 2,$ we have the following results:

.1-2 Full Alternative Text

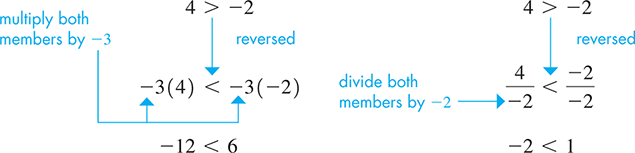
In Fig. 17.3, we see that 4 is to the right of $- 2,$ $- 2,$ but that $- 12$ $- 12$ is to the left of 6 and that $- 2$ $- 2$ is to the left of 1. This is consistent with reversing the sense of the inequality when it is multiplied by $- 3$ $- 3$ and when it is divided by $- 2.$ $- 2.$

A number line with closed circles at negative 12, negative 2, 1, 4, and 6 from left to right. — Fig. 17.3

If both members of an inequality are positive numbers and n is a positive integer, then the inequality formed by taking the nth power of each member, or the nth root of each member, is in the same sense as the given inequality. Symbolically, this is stated as “if $a > b,$ $a > b,$ then $a^{n} > b^{n},$ $a^{n} > b^{n},$ and $\sqrt[n]{a} > \sqrt[n]{b},$ $\sqrt[n]{a} > \sqrt[n]{b},$ provided that $n > 0, a > 0, b > 0.$ $n > 0, a > 0, b > 0.$ ”

EXAMPLE 8 Illustrations of property 4

Using property 4 on the inequality $16 > 9,$ $16 > 9,$ we have

\begin{array}{c} 16 > 9 & 16 > 9 \\ square both members & take square root of both members \\ 16^{2} > 9^{2} & \sqrt{16} > \sqrt{9} \\ 256 > 81 & 4 > 3 \end{array}

$\begin{array}{c} 16 > 9 & 16 > 9 \\ square both members & take square root of both members \\ 16^{2} > 9^{2} & \sqrt{16} > \sqrt{9} \\ 256 > 81 & 4 > 3 \end{array}$

Many inequalities have more than two members. In fact, inequalities with three members are common, and care must be used in stating these inequalities.

EXAMPLE 9 Inequalities with three members

To state that 5 is less than 6, and also greater than 2, we may write $2 < 5 < 6,$ $2 < 5 < 6,$ or $6 > 5 > 2.$ $6 > 5 > 2.$ (Generally, the less than form is preferred.)
To state that a number x may be greater than $- 1$ $- 1$ and also less than or equal to 3, we write $- 1 < x \leq 3.$ $- 1 < x \leq 3.$ (It can also be written as $x > - 1$ $x > - 1$ and $x \leq 3.$ $x \leq 3.$ ) This is shown in Fig. 17.4(a). Note the use of the open circle and the solid circle.
By writing $x \leq - 4$ $x \leq - 4$ or $x > 2,$ $x > 2,$ we state that x is less than or equal to $- 4,$ $- 4,$ or greater than 2. It may not be shown as $2 < x \leq - 4,$ $2 < x \leq - 4,$ for this shows x as being less than $- 4,$ $- 4,$ and also greater than 2, and no such numbers exist. See Fig. 17.4(b).

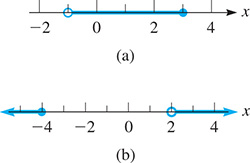
Two number lines. Number line ay is shaded between an open circle at 1 and closed circle at 3. Number line b is shaded left of a closed circle at 4, and right of an open circle at 2. — Fig. 17.4

NOTE

[Note carefully that and is used when the solution consists of values that make both statements true. The word or is used when the solution consists of values that make either statement true.]

(In everyday speech, or can sometimes mean that one statement is true or another statement is true, but not that both are true.)

EXAMPLE 10 Meaning of and—meaning of or

The inequality $x^{2} - 3 x + 2 > 0$ $x^{2} - 3 x + 2 > 0$ is satisfied if x is either greater than 2 or less than 1. This is written as $x > 2$ $x > 2$ or $x < 1,$ $x < 1,$ but it is incorrect to state it as $1 > x > 2.$ $1 > x > 2.$ (If we wrote it this way, we would be saying that the same value of x is less than 1 and at the same time greater than 2. Of course, as noted for this type of situation in Example 9, no such number exists.) However, we could say that the inequality is not satisfied for $1 \leq x \leq 2,$ $1 \leq x \leq 2,$ which means those values of x greater than or equal to 1 and less than or equal to 2 (between or equal to 1 and 2).

EXAMPLE 11 Setting up an inequality— solar panel design

The design of a rectangular solar panel shows that the length l is between 80 cm and 90 cm and the width w is between 40 cm and 80 cm. See Fig. 17.5. Find the values of area the panel may have.

Because l is to be less than 90 cm and w less than 80 cm, the area must be less than $(90 cm) (80 cm) = {7200 cm}^{2} .$ $(90 cm) (80 cm) = {7200 cm}^{2} .$ Also, because l is to be greater than 80 cm and w greater than 40 cm, the area must be greater than $(80 cm) (40 cm) = {3200 cm}^{2} .$ $(80 cm) (40 cm) = {3200 cm}^{2} .$ Therefore, the area A may be represented as

{3200 cm}^{2} < A < {7200 cm}^{2}

${3200 cm}^{2} < A < {7200 cm}^{2}$

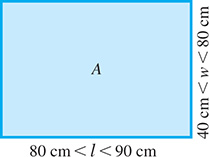
A rectangle labeled A with length 80 centimeters less than l less than 90 centimeters, and width 40 centimeters less than w less than 80 centimeters is displayed. — Fig. 17.5

This means the area is greater than ${3200 cm}^{2}$ ${3200 cm}^{2}$ and less than ${7200 cm}^{2} .$ ${7200 cm}^{2} .$

EXAMPLE 12 Setting up an inequality—current through diode

A semiconductor diode has the property that an electric current flows through it in only one direction. If it is an alternating-current circuit, the current in the circuit flows only during the half-cycle when the diode allows it to flow. If a source of current given by $i = 2 \sin π t$ $i = 2 \sin π t$ (i in mA, t in seconds) is connected in series with a diode, write the inequalities for the current and the time. Assume the source is on for 3.0 s and a positive current passes through the diode.

We are to find the values of t that correspond to $i > 0.$ $i > 0.$ From the properties of the sine function, we know that $2 \sin π t$ $2 \sin π t$ has a period of $2 π / π = 2.0 s .$ $2 π / π = 2.0 s .$ Therefore, the current is zero for $t = 0,$ $t = 0,$ 1.0 s, 2.0 s, and 3.0 s.

The source current is positive for $0 < t < 1.0 s$ $0 < t < 1.0 s$ and for $2.0 s < t < 3.0 s .$ $2.0 s < t < 3.0 s .$
The source current is negative for $1.0 s < t < 2.0 s .$ $1.0 s < t < 2.0 s .$
Therefore, in the circuit

\begin{array}{c} i > 0 for 0 < t < 1.0 s and 2.0 s < t < 3.0 s \\ i = 0 for t = 0, 1.0 s \leq t \leq 2.0 s \end{array}

$\begin{array}{c} i > 0 for 0 < t < 1.0 s and 2.0 s < t < 3.0 s \\ i = 0 for t = 0, 1.0 s \leq t \leq 2.0 s \end{array}$

A graph of the current in the circuit as a function of time is shown in Fig. 17.6(a). In Fig. 17.6(b), the values of t for which $i > 0$ $i > 0$ are shown.

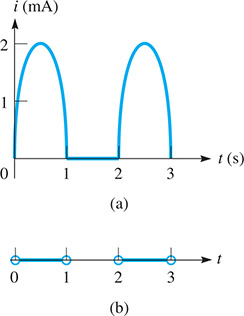
2 diagrams illustrate current flow in a semiconductor diode. — Fig. 17.6

Figure 17.6 Full Alternative Text

EXERCISES 17.1

In Exercises 1–4, make the given changes in the indicated examples of this section and then perform the indicated operations.

In Example 2, in the first paragraph, change the $>$ $>$ to $<$ $<$ and then complete the meaning of the resulting inequality as in the first sentence. Rewrite the meaning as in the second line.
In Example 4(b), change $\leq$ $\leq$ to $>$ $>$ and then graph the resulting inequality.
In Example 7, change the inequality to $- 2 > - 4$ $- 2 > - 4$ and then perform the two operations shown in color.
In Example 9(b), change the $- 1$ $- 1$ to $- 3$ $- 3$ and the 3 to 1 and then write the two forms in which an inequality represents the statement.

In Exercises 5–12, for the inequality $4 < 9,$ $4 < 9,$ state the inequality that results when the given operations are performed on both members.

Add 5.
Subtract 16.
Multiply by 4.
Multiply by $- 2.$ $- 2.$
Divide by $- 1.$ $- 1.$
Divide by 0.5.
Square both.
Take square roots.

In Exercises 13–24, give the inequalities equivalent to the following statements about the number x.

Greater than $- 2$ $- 2$
Less than 0.7
Less than or equal to 38
Greater than or equal to $- 6$ $- 6$
Greater than 1 and less than 7
Greater than or equal to $- 200$ $- 200$ and less than 650
Less than $- 5,$ $- 5,$ or greater than or equal to $3$ $3$
Less than or equal to 8, or greater than or equal to 12
Less than 1, or greater than 3 and less than or equal to 5
Greater than or equal to 0 and less than or equal to 2, or greater than 5
Greater than $- 2$ $- 2$ and less than 2, or greater than or equal to 3 and less than 4
Less than $- 4,$ $- 4,$ or greater than or equal to 0 and less than or equal to 1, or greater than or equal to 5

In Exercises 25–28, give verbal statements equivalent to the given inequalities involving the number x.

$0 < x \leq 9$ $0 < x \leq 9$
$x < 5$ $x < 5$ or $x > 7$ $x > 7$
$x < - 10$ $x < - 10$ or $10 \leq x < 20$ $10 \leq x < 20$
$- 1 \leq x < 3$ $- 1 \leq x < 3$ or $5 < x < 7$ $5 < x < 7$

In Exercises 29–44, graph the given inequalities on the number line.

$x < 3$ $x < 3$
$x \geq - 1$ $x \geq - 1$
$x \leq - 1$ $x \leq - 1$ or $x > 0.5$ $x > 0.5$
$x < - 300$ $x < - 300$ or $x \geq 0$ $x \geq 0$
$0 \leq x < 5$ $0 \leq x < 5$
$- 4 < y < - 2$ $- 4 < y < - 2$
$x \geq - 3$ $x \geq - 3$ and $x < 5$ $x < 5$
$x > 4$ $x > 4$ and $x < 3$ $x < 3$
$x < - 1$ $x < - 1$ or $1 \leq x < 4$ $1 \leq x < 4$
$- 3 < x < 0$ $- 3 < x < 0$ or $x > 3$ $x > 3$
$- 3 < x < - 1$ $- 3 < x < - 1$ or $0.5 < x \leq 3$ $0.5 < x \leq 3$
$x \leq 4$ $x \leq 4$ or $x > - 4$ $x > - 4$
$t \leq - 5$ $t \leq - 5$ and $t \geq - 5$ $t \geq - 5$
$x < 1$ $x < 1$ or $1 < x \leq 4$ $1 < x \leq 4$
$\begin{array}{l} (\begin{array}{l} x \leq 5 & or & x \geq 8 \end{array}) & and & (3 < x < 10) \end{array}$ $\begin{array}{l} (\begin{array}{l} x \leq 5 & or & x \geq 8 \end{array}) & and & (3 < x < 10) \end{array}$
$\begin{array}{l} (\begin{array}{l} x < 7 & and & x > 2 \end{array}) & and & (\begin{array}{l} x \geq 10 & or & x < 1 \end{array}) \end{array}$ $\begin{array}{l} (\begin{array}{l} x < 7 & and & x > 2 \end{array}) & and & (\begin{array}{l} x \geq 10 & or & x < 1 \end{array}) \end{array}$

In Exercises 45–48, answer the given questions about the inequality $0 < a < b .$ $0 < a < b .$

Is $a^{2} < b^{2}$ $a^{2} < b^{2}$ a conditional inequality or an absolute inequality?
Is $| a - b | < b - a ?$ $| a - b | < b - a ?$
If each member of the inequality $2 > 1$ $2 > 1$ is multiplied by $a - b,$ $a - b,$ is the result $2 (a - b) > (a - b) ?$ $2 (a - b) > (a - b) ?$
What is wrong with the following sequence of steps?

$a < b, a b < b^{2}, a b - b^{2} < 0, b (a - b) < 0, b < 0$ $a < b, a b < b^{2}, a b - b^{2} < 0, b (a - b) < 0, b < 0$

In Exercises 49–52, solve the given problems.

Write the relationship between $(| x | + | y |)$ $(| x | + | y |)$ and $| x + y |$ $| x + y |$ if $x > 0$ $x > 0$ and $y < 0.$ $y < 0.$
Write the relationship between $| x y |$ $| x y |$ and $| x | | y |$ $| x | | y |$ if $x > 0$ $x > 0$ and $y < 0.$ $y < 0.$
Explain the error in the following “proof” that $3 < 2 :$ $3 < 2 :$
1. $1/8 < 1/4$ $1/8 < 1/4$
2. ${0.5}^{3} < {0.5}^{2}$ ${0.5}^{3} < {0.5}^{2}$
3. $\log {0.5}^{3} < \log {0.5}^{2}$ $\log {0.5}^{3} < \log {0.5}^{2}$
4. $3 \log 0.5 < 2 \log 0.5$ $3 \log 0.5 < 2 \log 0.5$
5. $3 < 2$ $3 < 2$
If $x \neq y,$ $x \neq y,$ show that $x^{2} + y^{2} > 2 x y .$ $x^{2} + y^{2} > 2 x y .$

In Exercises 53–62, some applications of inequalities are shown.

The length L and width w (in yd) of a rectangular soccer field should satisfy the inequalities $110 \leq L \leq 120$ $110 \leq L \leq 120$ and $70 \leq w \leq 80.$ $70 \leq w \leq 80.$ Express the possible diagonal lengths d as an inequality.
A breakfast cereal company guarantees the calorie count shown for each serving is accurate within 5%. If the package shows a serving has 200 cal, write an inequality for the possible calorie counts.
An electron microscope can magnify an object from 2000 times to 1,000,000 times. Assuming these values are exact, express these magnifications M as an inequality and graph them.
A busy person glances at a digital clock that shows 9:36. Another glance a short time later shows the clock at 9:44. Express the amount of time t (in min) that could have elapsed between glances by use of inequalities. Graph these values of t.
An Earth satellite put into orbit near Earth’s surface will have an elliptic orbit if its velocity v is between 18,000 mi/h and 25,000 mi/h. Write this as an inequality and graph these values of v.
Fossils found in Jurassic rocks indicate that dinosaurs flourished during the Jurassic geological period, 140 MY (million years ago) to 200 MY. Write this as an inequality, with t representing past time. Graph the values of t.
A DVD player spins at 1530 r/min at the innermost edge and gradually slows to a rate of 630 r/min at the outer edge. Use an inequality to express the angular velocity $ω$ $ω$ of the DVD player.
The velocity v of an ultrasound wave in soft human tissue may be represented as $1550 \pm 60 m / s,$ $1550 \pm 60 m / s,$ where the $\pm 60 m / s$ $\pm 60 m / s$ gives the possible variation in the velocity. Express the possible velocities by an inequality.
A driver using the Google Maps app finds that it is 300 mi to her destination. If her speed always stays between 50 mi/h and 60 mi/h, use an inequality to express the required time t for the trip.
If the current from the source in Example 12 is $i = 5 \cos 4 π t$ $i = 5 \cos 4 π t$ and the diode allows only negative current to flow, write the inequalities and draw the graph for the current in the circuit as a function of time for $0 \leq t \leq 1 s .$ $0 \leq t \leq 1 s .$

Answers to Practice Exercises

$2 < 11$ $2 < 11$
$- 14 < - 5$ $- 14 < - 5$
$- 24 < 12$ $- 24 < 12$
$2 > - 1$ $2 > - 1$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 17.1 Properties of Inequalities

Create new playlist

Sign In

Sign Up

Table of Contents for
17.1 Properties of Inequalities