Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

20.3 Double-Angle Formulas

Formula for $\sin 2 α$ $\sin 2 α$ • Formulas for $\cos 2 α$ $\cos 2 α$ • Formula for $\tan 2 α$ $\tan 2 α$

If we let $β = α$ $β = α$ in the sum formulas for sine, cosine, and tangent (given in Section 20.2), we can derive the important double-angle formulas:

\begin{array}{rcl} \sin (α + α) & = & \sin (2 α) = \sin α \cos α + \cos α \sin α = 2 \sin α \cos α \\ \cos (α + α) & = & \cos α \cos α - \sin α \sin α = \cos^{2} α - \sin^{2} α \\ \tan (α + α) & = & \frac{\tan α + \tan α}{1 - \tan α \tan α} = \frac{2 \tan α}{1 - \tan^{2} α} \end{array}

$\begin{array}{rcl} \sin (α + α) & = & \sin (2 α) = \sin α \cos α + \cos α \sin α = 2 \sin α \cos α \\ \cos (α + α) & = & \cos α \cos α - \sin α \sin α = \cos^{2} α - \sin^{2} α \\ \tan (α + α) & = & \frac{\tan α + \tan α}{1 - \tan α \tan α} = \frac{2 \tan α}{1 - \tan^{2} α} \end{array}$

Then using the basic identity $\sin^{2} x + \cos^{2} x = 1,$ $\sin^{2} x + \cos^{2} x = 1,$ other forms of the equation for $\cos 2 α$ $\cos 2 α$ may be derived. Summarizing these forms, we have

\sin 2 α = 2 \sin α \cos α

$\sin 2 α = 2 \sin α \cos α$ (20.21)

\cos 2 α = \cos^{2} α - \sin^{2} α

$\cos 2 α = \cos^{2} α - \sin^{2} α$ (20.22)

= 2 \cos^{2} α - 1

$= 2 \cos^{2} α - 1$ (20.23)

= 1 - 2 \sin^{2} α

$= 1 - 2 \sin^{2} α$ (20.24)

\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}

$\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$ (20.25)

These double-angle formulas are widely used in applications of trigonometry, especially in calculus. They should be recognized quickly in any of the above forms.

CAUTION

Note carefully that $\sin 2 α$ $\sin 2 α$ IS NOT $2 \sin α .$ $2 \sin α .$

EXAMPLE 1 Using double-angle formulas

If $α = 30 °,$ $α = 30 °,$ we have

$\begin{array}{l} \cos 60 ° = \cos 2 (30 °) = \cos^{2} 30 ° - \sin^{2} 30 ° = {(\frac{\sqrt{3}}{2})}^{2} - {(\frac{1}{2})}^{2} = \frac{1}{2} & \begin{array}{l} using Eq . \\ (20.22) \end{array} \end{array}$ $\begin{array}{l} \cos 60 ° = \cos 2 (30 °) = \cos^{2} 30 ° - \sin^{2} 30 ° = {(\frac{\sqrt{3}}{2})}^{2} - {(\frac{1}{2})}^{2} = \frac{1}{2} & \begin{array}{l} using Eq . \\ (20.22) \end{array} \end{array}$
If $α = 3 x,$ $α = 3 x,$ we have

$\sin 6 x = \sin 2 (3 x) = 2 \sin 3 x \cos 3 x using Eq . (20.21)$ $\sin 6 x = \sin 2 (3 x) = 2 \sin 3 x \cos 3 x using Eq . (20.21)$
If $2 α = x,$ $2 α = x,$ we may write $α = x / 2,$ $α = x / 2,$ which means that

$\sin x = \sin 2 (\frac{x}{2}) = 2 \sin \frac{x}{2} \cos \frac{x}{2} using Eq . (20.21)$ $\sin x = \sin 2 (\frac{x}{2}) = 2 \sin \frac{x}{2} \cos \frac{x}{2} using Eq . (20.21)$
If $α = \frac{π}{6},$ $α = \frac{π}{6},$ we have

$\tan \frac{π}{3} = \tan 2 (\frac{π}{6}) = \frac{2 \tan \frac{π}{6}}{1 - \tan^{2} (\frac{π}{6})} = \frac{2 (\sqrt{3} / 3)}{1 - {(\sqrt{3} / 3)}^{2}} = \sqrt{3} using Eq . (20.25)$ $\tan \frac{π}{3} = \tan 2 (\frac{π}{6}) = \frac{2 \tan \frac{π}{6}}{1 - \tan^{2} (\frac{π}{6})} = \frac{2 (\sqrt{3} / 3)}{1 - {(\sqrt{3} / 3)}^{2}} = \sqrt{3} using Eq . (20.25)$

EXAMPLE 2 Simplification using cos 2`α` formula

Simplify the expression $\cos^{2} 2 x - \sin^{2} 2 x .$ $\cos^{2} 2 x - \sin^{2} 2 x .$

Since this is the difference of the square of the cosine of an angle and the square of the sine of the same angle, it fits the right side of Eq. (20.22). Therefore, letting $α = 2 x,$ $α = 2 x,$ we have

\cos^{2} 2 x - \sin^{2} 2 x = \cos 2 (2 x) = \cos 4 x

$\cos^{2} 2 x - \sin^{2} 2 x = \cos 2 (2 x) = \cos 4 x$

EXAMPLE 3 Using sin 2`α` formula—area of land

To find the area A of a right triangular tract of land, a surveyor may use the formula $A = \frac{1}{4} c^{2} \sin 2 θ,$ $A = \frac{1}{4} c^{2} \sin 2 θ,$ where c is the hypotenuse and $θ$ $θ$ is either of the acute angles. Derive this formula.

In Fig. 20.15, we see that $\sin θ = a / c$ $\sin θ = a / c$ and $\cos θ = b / c,$ $\cos θ = b / c,$ which gives us

A right triangle with area Ay has leg b, leg ay, and hypotenuse c. Opposite leg ay is angle theta. — Fig. 20.15

a = c \sin θ and b = c \cos θ

$a = c \sin θ and b = c \cos θ$

The area is given by $A = \frac{1}{2} a b,$ $A = \frac{1}{2} a b,$ which leads to the solution

\begin{array}{rcll} A & = & \frac{1}{2} a b = \frac{1}{2} (c \sin θ) (c \cos θ) \\ = & \frac{1}{2} c^{2} \sin θ \cos θ = \frac{1}{2} c^{2} (\frac{1}{2} \sin 2 θ) & using Eq . (20.21) \\ = & \frac{1}{4} c^{2} \sin 2 θ \end{array}

$\begin{array}{rcll} A & = & \frac{1}{2} a b = \frac{1}{2} (c \sin θ) (c \cos θ) \\ = & \frac{1}{2} c^{2} \sin θ \cos θ = \frac{1}{2} c^{2} (\frac{1}{2} \sin 2 θ) & using Eq . (20.21) \\ = & \frac{1}{4} c^{2} \sin 2 θ \end{array}$

In using Eq. (20.21), we divided both sides by 2 to get $\sin θ \cos θ = \frac{1}{2} \sin 2 θ .$ $\sin θ \cos θ = \frac{1}{2} \sin 2 θ .$

If we had labeled the upper acute angle in Fig. 20.15 as $θ,$ $θ,$ we would have $a = c \cos θ$ $a = c \cos θ$ and $b = c \sin θ .$ $b = c \sin θ .$ Using these values in the formula for the area gives the same solution.

EXAMPLE 4 Verifying values

Verifying the values of $\sin 90 °$ $\sin 90 °$ , using the functions of $45 °$ $45 °$ , we have

$\begin{array}{l} \sin 90 ° = \sin 2 (45 °) = 2 \sin 45 ° \cos 45 ° = 2 (\frac{\sqrt{2}}{2}) (\frac{\sqrt{2}}{2}) = 1 & \begin{array}{l} using Eq . \\ (20.21) \end{array} \end{array}$ $\begin{array}{l} \sin 90 ° = \sin 2 (45 °) = 2 \sin 45 ° \cos 45 ° = 2 (\frac{\sqrt{2}}{2}) (\frac{\sqrt{2}}{2}) = 1 & \begin{array}{l} using Eq . \\ (20.21) \end{array} \end{array}$
Using Eq. (20.25), $\tan 142 ° = \frac{2 \tan 71 °}{1 - \tan^{2} 71 °} .$ $\tan 142 ° = \frac{2 \tan 71 °}{1 - \tan^{2} 71 °} .$ Using a calculator, we have

$\tan 142 ° = - 0.7812856265 and \frac{2 \tan 71 °}{1 - \tan^{2} 71 °} = - 0.7812856265$ $\tan 142 ° = - 0.7812856265 and \frac{2 \tan 71 °}{1 - \tan^{2} 71 °} = - 0.7812856265$

EXAMPLE 5 Evaluation using sin 2`α` formula

If $\cos α = \frac{3}{5}$ $\cos α = \frac{3}{5}$ for a fourth-quadrant angle, from Fig. 20.16(a) we see that $\sin α = - \frac{4}{5} .$ $\sin α = - \frac{4}{5} .$ Thus,

Figure 20.16 Full Alternative Text

\begin{array}{rcll} \sin 2 α & = & 2 \sin α \cos α & Eq . (20.21) \\ = & 2 (- \frac{4}{5}) (\frac{3}{5}) = - \frac{24}{25} \end{array}

$\begin{array}{rcll} \sin 2 α & = & 2 \sin α \cos α & Eq . (20.21) \\ = & 2 (- \frac{4}{5}) (\frac{3}{5}) = - \frac{24}{25} \end{array}$

In Fig. 20.16(b), angle $2 α$ $2 α$ is shown to be in the third-quadrant, verifying the sign of the result. ( $\cos α = 3/5, α = 307 °, 2 α = 614 °,$ $\cos α = 3/5, α = 307 °, 2 α = 614 °,$ which is a third-quadrant angle.)

EXAMPLE 6 Simplification using cos 2`α`

Simplify the expression $\frac{2}{1 + \cos 2 x} .$ $\frac{2}{1 + \cos 2 x} .$

\begin{array}{rcll} \frac{2}{1 + \cos 2 x} & = & \frac{2}{1 + (2 \cos^{2} x - 1)} & using Eq . (20.2) \\ = & \frac{2}{2 \cos^{2} x} = \sec^{2} x & using Eq . (20.23) \end{array}

$\begin{array}{rcll} \frac{2}{1 + \cos 2 x} & = & \frac{2}{1 + (2 \cos^{2} x - 1)} & using Eq . (20.2) \\ = & \frac{2}{2 \cos^{2} x} = \sec^{2} x & using Eq . (20.23) \end{array}$

EXAMPLE 7 Trig identity—calculator verification

Prove the identity $\frac{\sin 3 x}{\sin x} + \frac{\cos 3 x}{\cos x} = 4 \cos 2 x .$ $\frac{\sin 3 x}{\sin x} + \frac{\cos 3 x}{\cos x} = 4 \cos 2 x .$

Because the left side is the more complex side, we change it to the form on the right:

\begin{array}{rcll} \frac{\sin 3 x}{\sin x} + \frac{\cos 3 x}{\cos x} & = & \frac{\sin 3 x \cos x + \cos 3 x \sin x}{\sin x \cos x} & combining fractions \\ = & \frac{\sin (3 x + x)}{\frac{1}{2} \sin 2 x} \begin{array}{l} \leftarrow & using Eq . (20.9) \\ \leftarrow & using Eq . (20.21) \end{array} \\ = & \frac{2 \sin 4 x}{\sin 2 x} = \frac{2 (2 \sin 2 x \cos 2 x)}{\sin 2 x} & using Eq . (20.21) \\ = & 4 \cos 2 x \end{array}

$\begin{array}{rcll} \frac{\sin 3 x}{\sin x} + \frac{\cos 3 x}{\cos x} & = & \frac{\sin 3 x \cos x + \cos 3 x \sin x}{\sin x \cos x} & combining fractions \\ = & \frac{\sin (3 x + x)}{\frac{1}{2} \sin 2 x} \begin{array}{l} \leftarrow & using Eq . (20.9) \\ \leftarrow & using Eq . (20.21) \end{array} \\ = & \frac{2 \sin 4 x}{\sin 2 x} = \frac{2 (2 \sin 2 x \cos 2 x)}{\sin 2 x} & using Eq . (20.21) \\ = & 4 \cos 2 x \end{array}$

We can check this identity by comparing the graphs of

y_{1} = (\sin 3 x) / (\sin x) + (\cos 3 x) / (\cos x) and y_{2} = 4 \cos 2 x .

$y_{1} = (\sin 3 x) / (\sin x) + (\cos 3 x) / (\cos x) and y_{2} = 4 \cos 2 x .$

Figure 20.17 shows the graph of $y_{2}$ $y_{2}$ (in red) being plotted over the graph of $y_{1}$ $y_{1}$ (in blue).

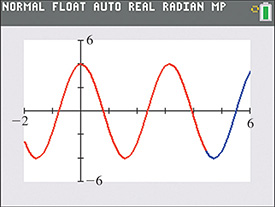
A curve oscillates about y = 0 with amplitude 4, period pi, and maximum (pi, 4). Part of the curve is red and part is blue. — Fig. 20.17

EXERCISES 20.3

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 1(d), change $\frac{π}{6}$ $\frac{π}{6}$ to $\frac{π}{3}$ $\frac{π}{3}$ and then evaluate $\tan \frac{2 π}{3} .$ $\tan \frac{2 π}{3} .$
In Example 2, change 2x to 3x and then simplify.
In Example 5, change 3/5 to 4/5 and then evaluate $\sin 2 α .$ $\sin 2 α .$
In Example 6, change the $+$ $+$ in the denominator to $-$ $-$ and then simplify the expression on the left.

In Exercises 5–8, determine the values of the indicated functions in the given manner.

Find $\sin 60 °$ $\sin 60 °$ by using the functions of $30 °$ $30 °$ .
Find $\sin 120 °$ $\sin 120 °$ by using the functions of $60 °$ $60 °$ .
Find $\tan 120 °$ $\tan 120 °$ by using the functions of $60 °$ $60 °$ .
Find $\cos 60 °$ $\cos 60 °$ by using the functions of $30 °$ $30 °$ .

In Exercises 9–14, use a calculator to verify the values found by using the double-angle formulas.

Find $\sin 100 °$ $\sin 100 °$ directly and by using functions of $50 °$ $50 °$ .
Find $\tan 184 °$ $\tan 184 °$ directly and by using functions of $92 °$ $92 °$ .
Find $\cos 96 °$ $\cos 96 °$ directly and by using functions of $48 °$ $48 °$ .
Find $\cos 276 °$ $\cos 276 °$ directly and by using functions of $138 °$ $138 °$ .
Find $\tan \frac{2 π}{7}$ $\tan \frac{2 π}{7}$ directly and by using functions of $\frac{π}{7} .$ $\frac{π}{7} .$
Find $\sin 1.2 π$ $\sin 1.2 π$ directly and by using functions of $0.6 π .$ $0.6 π .$

In Exercises 15–18, evaluate the indicated functions with the given information.

Find sin 2x if $\cos x = \frac{4}{5}$ $\cos x = \frac{4}{5}$ (in first quadrant).
Find cos 2x if $\sin x = - \frac{12}{13}$ $\sin x = - \frac{12}{13}$ (in third quadrant).
Find tan 2x if $\sin x = 0.5$ $\sin x = 0.5$ (in second quadrant).
Find sin 4x if $\tan x = - 0.6$ $\tan x = - 0.6$ (in fourth quadrant).

In Exercises 19–30, simplify the given expressions.

6 sin 5x cos 5x
$4 \sin^{2} {x \cos}^{2} x$ $4 \sin^{2} {x \cos}^{2} x$
$1 - 2 \sin^{2} 4 x$ $1 - 2 \sin^{2} 4 x$
$\frac{4 \tan 4 θ}{1 - \tan^{2} 4 θ}$ $\frac{4 \tan 4 θ}{1 - \tan^{2} 4 θ}$
$2 \cos^{2} \frac{1}{2} x - 1$ $2 \cos^{2} \frac{1}{2} x - 1$
$4 \sin \frac{1}{2} x \cos \frac{1}{2} x$ $4 \sin \frac{1}{2} x \cos \frac{1}{2} x$
$8 \sin^{2} 2 x - 4$ $8 \sin^{2} 2 x - 4$
6 cos 3x sin 3x
$\frac{\sin 6 θ}{\cos 3 θ}$ $\frac{\sin 6 θ}{\cos 3 θ}$
$\cos^{4} u - \sin^{4} u$ $\cos^{4} u - \sin^{4} u$
$\frac{\sin 3 x}{\sin x} - \frac{\cos 3 x}{\cos x}$ $\frac{\sin 3 x}{\sin x} - \frac{\cos 3 x}{\cos x}$
$\frac{\cos 3 x}{\sin x} + \frac{\sin 3 x}{\cos x}$ $\frac{\cos 3 x}{\sin x} + \frac{\sin 3 x}{\cos x}$

In Exercises 31–40, prove the given identities.

$\cos^{2} α - \sin^{2} α = 2 \cos^{2} α - 1$ $\cos^{2} α - \sin^{2} α = 2 \cos^{2} α - 1$
$\cos^{2} α - \sin^{2} α = 1 - 2 \sin^{2} α$ $\cos^{2} α - \sin^{2} α = 1 - 2 \sin^{2} α$
$\frac{\cos x - \tan x \sin x}{\sec x} = \cos 2 x$ $\frac{\cos x - \tan x \sin x}{\sec x} = \cos 2 x$
$2 + \frac{\cos 2 θ}{\sin^{2} θ} = \csc^{2} θ$ $2 + \frac{\cos 2 θ}{\sin^{2} θ} = \csc^{2} θ$
$\frac{\sin 2 θ}{1 + \cos 2 θ} = \tan θ$ $\frac{\sin 2 θ}{1 + \cos 2 θ} = \tan θ$
$\frac{2 \tan α}{1 + \tan^{2} α} = \sin 2 α$ $\frac{2 \tan α}{1 + \tan^{2} α} = \sin 2 α$
$1 - \cos 2 θ = \frac{2}{1 + \cot^{2} θ}$ $1 - \cos 2 θ = \frac{2}{1 + \cot^{2} θ}$
$\frac{\cos^{3} θ + \sin^{3} θ}{\cos θ + \sin θ} = 1 - \frac{1}{2} \sin 2 θ$ $\frac{\cos^{3} θ + \sin^{3} θ}{\cos θ + \sin θ} = 1 - \frac{1}{2} \sin 2 θ$
$\ln (1 - \cos 2 x) - \ln (1 + \cos 2 x) = 2 \ln \tan x$ $\ln (1 - \cos 2 x) - \ln (1 + \cos 2 x) = 2 \ln \tan x$
$\log (20 \sin^{2} θ + 10 \cos 2 θ) = 1$ $\log (20 \sin^{2} θ + 10 \cos 2 θ) = 1$

In Exercises 41–44, verify each identity by comparing the graph of the left side with the graph of the right side on a calculator.

$\tan 2 θ = \frac{2}{\cot θ - \tan θ}$ $\tan 2 θ = \frac{2}{\cot θ - \tan θ}$
$\frac{1 - \tan^{2} x}{\sec^{2} x} = \cos 2 x$ $\frac{1 - \tan^{2} x}{\sec^{2} x} = \cos 2 x$
${(\sin x + \cos x)}^{2} = 1 + \sin 2 x$ ${(\sin x + \cos x)}^{2} = 1 + \sin 2 x$
$2 \csc 2 x \tan x = \sec^{2} x$ $2 \csc 2 x \tan x = \sec^{2} x$

In Exercises 45–62, solve the given problems.

Express sin 3x in terms of sin x only.
Express cos 3x in terms of cos x only.
Express cos 4x in terms of cos x only.
Express sin 4x in terms of sin x and cos x.
Find the exact value of $\cos 2 x + \sin 2 x \tan x .$ $\cos 2 x + \sin 2 x \tan x .$
Find the exact value of $\cos^{4} x - \sin^{4} x - \cos 2 x .$ $\cos^{4} x - \sin^{4} x - \cos 2 x .$
Simplify: $\log (\cos x - \sin x) + \log (\cos x + \sin x) .$ $\log (\cos x - \sin x) + \log (\cos x + \sin x) .$
For an acute angle $θ,$ $θ,$ show that $2 \sin θ > \sin 2 θ .$ $2 \sin θ > \sin 2 θ .$
Without graphing, determine the amplitude and period of the function $y = 4 \sin x \cos x .$ $y = 4 \sin x \cos x .$ Explain.
Without graphing, determine the amplitude and period of the function $y = \cos^{2} x - \sin^{2} x .$ $y = \cos^{2} x - \sin^{2} x .$
The path of a bouncing ball is given by $y = \sqrt{{(\sin x + \cos x)}^{2}} .$ $y = \sqrt{{(\sin x + \cos x)}^{2}} .$ Show that this path can also be shown as $y = \sqrt{1 + \sin 2 x} .$ $y = \sqrt{1 + \sin 2 x} .$ Use a calculator to show that this can also be shown as $y = | \sin x + \cos x | .$ $y = | \sin x + \cos x | .$
The equation for the trajectory of a missile fired into the air at an angle $α$ $α$ with velocity $v_{0}$ $v_{0}$ is $y = x \tan α - \frac{g}{2 v_{0}^{2} \cos^{2} α} x^{2} .$ $y = x \tan α - \frac{g}{2 v_{0}^{2} \cos^{2} α} x^{2} .$ Here, g is the acceleration due to gravity. On the right of the equal sign, combine terms and simplify.
The CN Tower in Toronto is 553 m high, and has an observation deck at the 335-m level. How far from the top of the tower must a 553-m high helicopter be so that the angle subtended at the helicopter by the part of the tower above the deck equals the angle subtended at the helicopter below the deck? In Fig. 20.18 these are the angles $α$ $α$ and $β .$ $β .$

Fig. 20.18

Figure 20.18 Full Alternative Text
The cross section of a radio-wave reflector is defined by $x = \cos 2 θ, y = \sin θ .$ $x = \cos 2 θ, y = \sin θ .$ Find the relation between x and y by eliminating $θ .$ $θ .$
To find the horizontal range R of a projectile, the equation $R = v t \cos α$ $R = v t \cos α$ is used, where $α$ $α$ is the angle between the line of fire and the horizontal, v is the initial velocity of the projectile, and t is the time of flight. It can be shown that $t = (2 v \sin α) / g,$ $t = (2 v \sin α) / g,$ where g is the acceleration due to gravity. Show that $R = (v^{2} \sin 2 α) / g .$ $R = (v^{2} \sin 2 α) / g .$ See Fig. 20.19.

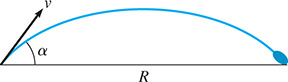
Fig. 20.19
In analyzing light reflection from a cylinder onto a flat surface, the expression $3 \cos θ - \cos 3 θ$ $3 \cos θ - \cos 3 θ$ arises. Show that this equals $2 \cos θ \cos 2 θ + 4 \sin θ \sin 2 θ .$ $2 \cos θ \cos 2 θ + 4 \sin θ \sin 2 θ .$
The instantaneous electric power p in an inductor is given by the equation $p = v i \sin ω t \sin (ω t - π / 2) .$ $p = v i \sin ω t \sin (ω t - π / 2) .$ Show that this equation can be written as $p = - \frac{1}{2} v i \sin 2 ω t .$ $p = - \frac{1}{2} v i \sin 2 ω t .$
In the study of the stress at a point in a bar, the equation $s = a \cos^{2} θ + b \sin^{2} θ - 2 t \sin θ \cos θ$ $s = a \cos^{2} θ + b \sin^{2} θ - 2 t \sin θ \cos θ$ arises. Show that this equation can be written as $s = \frac{1}{2} (a + b) + \frac{1}{2} (a - b) \cos 2 θ - t \sin 2 θ .$ $s = \frac{1}{2} (a + b) + \frac{1}{2} (a - b) \cos 2 θ - t \sin 2 θ .$

Answers to Practice Exercises

$\cos 90 ° = \cos^{2} 45 ° - \sin^{2} 45 ° = {(\frac{1}{2} \sqrt{2})}^{2} - {(\frac{1}{2} \sqrt{2})}^{2} = 0$ $\cos 90 ° = \cos^{2} 45 ° - \sin^{2} 45 ° = {(\frac{1}{2} \sqrt{2})}^{2} - {(\frac{1}{2} \sqrt{2})}^{2} = 0$
tan 2x

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 20.3 Double-Angle Formulas

Create new playlist

Sign In

Sign Up

Table of Contents for
20.3 Double-Angle Formulas